La rotordinámica (o dinámica de rotores ) es una rama especializada de la mecánica aplicada que se ocupa del comportamiento y el diagnóstico de las estructuras rotatorias . Se utiliza comúnmente para analizar el comportamiento de estructuras que van desde motores a reacción y turbinas de vapor hasta motores de automóviles y almacenamiento en disco de computadora . En su nivel más básico, la dinámica de rotores se ocupa de una o más estructuras mecánicas ( rotores ) sostenidas por cojinetes e influenciadas por fenómenos internos que giran alrededor de un solo eje . La estructura de soporte se llama estator . A medida que aumenta la velocidad de rotación, la amplitud de vibración a menudo pasa por un máximo que se llama velocidad crítica . Esta amplitud es comúnmente excitada por el desequilibrio de la estructura rotatoria; los ejemplos cotidianos incluyen el equilibrio del motor y el equilibrio de los neumáticos . Si la amplitud de vibración a estas velocidades críticas es excesiva, se produce una falla catastrófica . Además de esto, las turbomáquinas a menudo desarrollan inestabilidades que están relacionadas con la composición interna de la turbomáquina y que deben corregirse. Esta es la principal preocupación de los ingenieros que diseñan rotores grandes.
La maquinaria rotatoria produce vibraciones dependiendo de la estructura del mecanismo involucrado en el proceso. Cualquier falla en la máquina puede aumentar o excitar las firmas de vibración. El comportamiento de vibración de la máquina debido al desequilibrio es uno de los aspectos principales de la maquinaria rotatoria que debe estudiarse en detalle y considerarse durante el diseño. Todos los objetos, incluida la maquinaria rotatoria, exhiben una frecuencia natural dependiendo de la estructura del objeto. La velocidad crítica de una máquina rotatoria ocurre cuando la velocidad de rotación coincide con su frecuencia natural. La velocidad más baja a la que se encuentra por primera vez la frecuencia natural se denomina primera velocidad crítica, pero a medida que aumenta la velocidad, se ven velocidades críticas adicionales que son múltiplos de la frecuencia natural. Por lo tanto, minimizar el desequilibrio rotacional y las fuerzas externas innecesarias es muy importante para reducir las fuerzas generales que inician la resonancia . Cuando la vibración está en resonancia, crea una energía destructiva que debería ser la principal preocupación al diseñar una máquina rotatoria. El objetivo aquí debería ser evitar operaciones que estén cerca de la crítica y pasar de manera segura a través de ellas cuando se acelera o desacelera. Si se ignora este aspecto, podría producirse pérdida de equipos, desgaste excesivo de la maquinaria, roturas catastróficas irreparables o incluso lesiones humanas y pérdida de vidas.
La dinámica real de la máquina es difícil de modelar teóricamente. Los cálculos se basan en modelos simplificados que se asemejan a varios componentes estructurales ( modelos de parámetros concentrados ), ecuaciones obtenidas a partir de la resolución numérica de los modelos ( método de Rayleigh-Ritz ) y, finalmente, del método de elementos finitos (FEM), que es otro enfoque para modelar y analizar la máquina para frecuencias naturales. También existen algunos métodos analíticos, como el método de función de transferencia distribuida [1] , que puede generar frecuencias naturales analíticas y de forma cerrada, velocidades críticas y respuesta de masa desequilibrada. En cualquier prototipo de máquina se prueba para confirmar las frecuencias precisas de resonancia y luego se rediseña para asegurar que no se produzca resonancia.
La ecuación de movimiento , en forma matricial generalizada, para un rotor axialmente simétrico que gira a una velocidad de giro constante Ω es donde:
La matriz giroscópica G es proporcional a la velocidad de giro Ω . La solución general de la ecuación anterior implica vectores propios complejos que dependen de la velocidad de giro. Los especialistas en ingeniería en este campo se basan en el diagrama de Campbell para explorar estas soluciones.
Una característica interesante del sistema de ecuaciones rotordinámicas son los términos fuera de la diagonal de rigidez, amortiguamiento y masa. Estos términos se denominan rigidez de acoplamiento cruzado, amortiguamiento de acoplamiento cruzado y masa de acoplamiento cruzado. Cuando hay una rigidez de acoplamiento cruzado positiva, una deflexión provocará una fuerza de reacción opuesta a la dirección de la deflexión para hacer reaccionar la carga, y también una fuerza de reacción en la dirección del remolino positivo. Si esta fuerza es lo suficientemente grande en comparación con el amortiguamiento y la rigidez directos disponibles, el rotor será inestable. Cuando un rotor es inestable, normalmente será necesario apagar inmediatamente la máquina para evitar una falla catastrófica.
El rotor Jeffcott (nombrado en honor a Henry Homan Jeffcott), también conocido como rotor de Laval en Europa, es un modelo simplificado de parámetros concentrados que se utiliza para resolver estas ecuaciones. Un rotor Jeffcott consta de un eje flexible, sin masa y uniforme montado sobre dos cojinetes flexibles equidistantes de un disco masivo unido rígidamente al eje. La forma más simple del rotor restringe el disco a un plano ortogonal al eje de rotación. Esto limita la respuesta del rotor solo a la vibración lateral. Si el disco está perfectamente equilibrado (es decir, su centro geométrico y centro de masas coinciden), entonces el rotor es análogo a un oscilador no amortiguado de un solo grado de libertad bajo vibración libre. Si hay alguna distancia radial entre el centro geométrico y el centro de masas, entonces el rotor está desequilibrado, lo que produce una fuerza proporcional a la masa del disco, m , la distancia entre los dos centros (excentricidad, ε ) y la velocidad de giro del disco, Ω . Después de calcular la rigidez equivalente, k , del sistema, podemos crear la siguiente ecuación diferencial ordinaria lineal de segundo orden que describe la desviación radial del disco desde la línea central del rotor. [2]
Si graficamos la respuesta radial, veríamos una onda sinusoidal con frecuencia angular . Esta oscilación lateral se denomina "remolino" y, en este caso, depende en gran medida de la velocidad de giro. La velocidad de giro no solo influye en la amplitud de la función de forzamiento, sino que también puede producir una amplificación dinámica cerca de la frecuencia natural del sistema.
Si bien el rotor de Jeffcott es una herramienta útil para introducir conceptos rotordinámicos, es importante señalar que se trata de una idealización matemática que sólo se aproxima vagamente al comportamiento de los rotores del mundo real. [2]
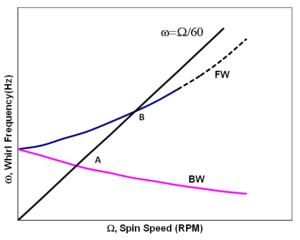
El diagrama de Campbell , también conocido como "Mapa de velocidad de giro" o "Diagrama de interferencia de frecuencia", de un sistema de rotor simple se muestra a la derecha. Las curvas rosa y azul muestran los modos de giro hacia atrás (BW) y hacia adelante (FW), respectivamente, que divergen a medida que aumenta la velocidad de giro. Cuando la frecuencia BW o la frecuencia FW son iguales a la velocidad de giro Ω, indicada por las intersecciones A y B con la línea de velocidad de giro sincrónica, la respuesta del rotor puede mostrar un pico. Esto se llama velocidad crítica .
La historia de la rotordinámica está repleta de interacciones entre teoría y práctica. WJM Rankine realizó por primera vez un análisis de un eje giratorio en 1869, pero su modelo no era adecuado y predijo que no se podrían alcanzar velocidades supercríticas. En 1895, Dunkerley publicó un artículo experimental que describía las velocidades supercríticas. Gustaf de Laval , un ingeniero sueco, hizo funcionar una turbina de vapor a velocidades supercríticas en 1889, y Kerr publicó un artículo que mostraba evidencia experimental de una segunda velocidad crítica en 1916.
La Royal Society de Londres encargó a Henry Jeffcott que resolviera el conflicto entre la teoría y la práctica. En 1919 publicó un artículo que ahora se considera un clásico en la revista Philosophical Magazine, en el que confirmaba la existencia de velocidades supercríticas estables. August Föppl publicó conclusiones muy similares en 1895, pero la historia ignoró en gran medida su trabajo.
Entre el trabajo de Jeffcott y el comienzo de la Segunda Guerra Mundial, se trabajó mucho en el área de inestabilidades y técnicas de modelado que culminaron en el trabajo de Nils Otto Myklestad [3] y MA Prohl [4], que condujo al método de matriz de transferencia (TMM) para analizar rotores. El método más utilizado hoy en día para el análisis de rotordinámica es el método de elementos finitos .
Los modelos informáticos modernos han sido comentados en una cita atribuida a Dara Childs: "la calidad de las predicciones de un código informático tiene más que ver con la solidez del modelo básico y la percepción física del analista ... Los algoritmos o códigos informáticos superiores no solucionarán los malos modelos o la falta de criterio de ingeniería".
El profesor F. Nelson ha escrito extensamente sobre la historia de la rotordinámica y la mayor parte de esta sección se basa en su trabajo.
Existen muchos paquetes de software capaces de resolver el sistema de ecuaciones de la dinámica de rotores. Los códigos específicos de la dinámica de rotores son más versátiles para fines de diseño. Estos códigos facilitan la incorporación de coeficientes de cojinetes, cargas laterales y muchos otros elementos que solo necesitaría un especialista en dinámica de rotores. Los códigos específicos de dinámica no de rotores son solucionadores de elementos finitos con todas las funciones y tienen muchos años de desarrollo en sus técnicas de resolución. Los códigos específicos de dinámica no de rotores también se pueden utilizar para calibrar un código diseñado para dinámica de rotores.
{{cite book}}: CS1 maint: multiple names: authors list (link)utiliza DyRoBeS{{cite book}}: CS1 maint: multiple names: authors list (link){{cite book}}: Enlace externo en |volume={{cite book}}: CS1 maint: multiple names: authors list (link){{cite book}}: CS1 maint: multiple names: authors list (link){{cite book}}: CS1 maint: multiple names: authors list (link){{cite book}}: CS1 maint: multiple names: authors list (link){{cite web}}: CS1 maint: archived copy as title (link)