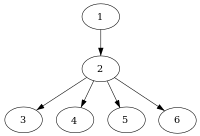
En informática , un nodo d de un gráfico de flujo de control domina a un nodo n si cada ruta desde el nodo de entrada hasta n debe pasar por d . En términos de notación, esto se escribe como d dom n (o, a veces, d ≫ n ). Por definición, cada nodo se domina a sí mismo.
Hay una serie de conceptos relacionados:
La dominancia fue introducida por primera vez por Reese T. Prosser en un artículo de 1959 sobre el análisis de diagramas de flujo. [2] Prosser no presentó un algoritmo para calcular la dominancia, que tuvo que esperar diez años hasta que Edward S. Lowry y CW Medlock lo hicieran. [3] Ron Cytron et al. reavivaron el interés en la dominancia en 1989 cuando la aplicaron al problema de calcular de manera eficiente la ubicación de las funciones φ, que se utilizan en forma de asignación simple estática . [4]
Los dominadores, y en particular las fronteras de dominancia, tienen aplicaciones en compiladores para calcular la forma de asignación única estática . Varias optimizaciones de compiladores también pueden beneficiarse de los dominadores. El diagrama de flujo en este caso comprende bloques básicos .
Los dominadores juegan un papel crucial en el análisis del flujo de control al identificar los comportamientos del programa que son relevantes para una declaración u operación específica, lo que ayuda a optimizar y simplificar el flujo de control de los programas para el análisis. [5]
La paralelización automática se beneficia de las fronteras de posdominancia. Este es un método eficiente para calcular la dependencia del control, que es fundamental para el análisis.
El análisis del uso de memoria puede beneficiarse del árbol dominador para encontrar fácilmente fugas e identificar un uso elevado de memoria. [6]
En los sistemas de hardware, los dominadores se utilizan para calcular probabilidades de señales para la generación de pruebas, estimar actividades de conmutación para el análisis de potencia y ruido y seleccionar puntos de corte en la verificación de equivalencia. [7] En los sistemas de software, se utilizan para reducir el tamaño del conjunto de pruebas en técnicas de pruebas estructurales como la cobertura de declaraciones y ramas. [8]
Sea el nodo de origen en el gráfico de flujo de control . Los dominadores de un nodo se dan mediante la solución máxima de las siguientes ecuaciones de flujo de datos:
El dominador del nodo de inicio es el propio nodo de inicio. El conjunto de dominadores de cualquier otro nodo es la intersección del conjunto de dominadores de todos los predecesores de . El nodo también está en el conjunto de dominadores de .
Un algoritmo para la solución directa es:
// el dominador del nodo de inicio es el inicio mismo Dom(n 0 ) = {n 0 } // Para todos los demás nodos, establezca todos los nodos como dominadores. para cada n en N - {n 0 } Dom(n) = N; // eliminar iterativamente los nodos que no sean dominadores mientras cambia en cualquier Dom(n) para cada n en N - {n 0 }: Dom(n) = {n} unión con intersección sobre Dom(p) para todo p en pred(n)La solución directa es cuadrática en el número de nodos, o O( n 2 ). Lengauer y Tarjan desarrollaron un algoritmo que es casi lineal, [1] y en la práctica, a excepción de unos pocos gráficos artificiales, el algoritmo y una versión simplificada del mismo son tan rápidos o más rápidos que cualquier otro algoritmo conocido para gráficos de todos los tamaños y su ventaja aumenta con el tamaño del gráfico. [9]
Keith D. Cooper , Timothy J. Harvey y Ken Kennedy de la Universidad Rice describen un algoritmo que esencialmente resuelve las ecuaciones de flujo de datos anteriores pero utiliza estructuras de datos bien diseñadas para mejorar el rendimiento. [10]
De manera análoga a la definición de dominancia anterior, se dice que un nodo z posdomina a un nodo n si todos los caminos hacia el nodo de salida del grafo que comienzan en n deben pasar por z . De manera similar, el posdominador inmediato de un nodo n es el posdominador de n que no posdomina estrictamente a ningún otro posdominador estricto de n .