Cuerda (estructura de datos)

Estructura de datos para almacenar cadenas

Una cuerda sencilla construida con la letra "Hola_mi_nombre_es_Simon".

En programación informática , una cuerda es una estructura de datos compuesta por cadenas más pequeñas que se utiliza para almacenar y manipular de manera eficiente cadenas más largas o textos completos. Por ejemplo, un programa de edición de texto puede utilizar una cuerda para representar el texto que se está editando, de modo que las operaciones como inserción, eliminación y acceso aleatorio se puedan realizar de manera eficiente. ^[1]

Descripción

Una cuerda es un tipo de árbol binario en el que cada hoja (nodo final) contiene una cadena y una longitud (también conocida como peso ), y cada nodo situado más arriba en el árbol contiene la suma de las longitudes de todas las hojas de su subárbol izquierdo . Un nodo con dos hijos divide la cadena completa en dos partes: el subárbol izquierdo almacena la primera parte de la cadena, el subárbol derecho almacena la segunda parte de la cadena y el peso de un nodo es la longitud de la primera parte.

En el caso típico de operaciones con cuerdas, se supone que las cadenas almacenadas en los nodos son objetos constantes e inmutables, lo que permite cierto comportamiento de copia al escribir . Los nodos de hoja suelen implementarse como cadenas básicas de longitud fija con un recuento de referencia adjunto para la desasignación cuando ya no se necesitan, aunque también se pueden utilizar otros métodos de recolección de basura .

Operaciones

En las siguientes definiciones, N es la longitud de la cuerda, es decir, el peso del nodo raíz.

Recoger hojas

Definición: Crea una pila S y una lista L. Recorre la columna más a la izquierda del árbol hasta llegar a una hoja l', añadiendo cada nodo n a S. Añade l' a L. El padre de l' ( p ) está en la parte superior de la pila. Repite el procedimiento para el subárbol derecho de p.

La clase final InOrderRopeIterator implementa Iterator < RopeLike > {      privado final Deque < RopeLike > pila ;    InOrderRopeIterator ( @NonNull RopeLike raíz ) { pila = new ArrayDeque <> (); var c = raíz ; mientras ( c != null ) { pila . push ( c ); c = c . getLeft (); } }                       @Override public boolean hasNext ( ) { return stack.size ( ) > 0 ; }          @Override public RopeLike next ( ) { val resultado = stack.pop () ;         si ( ! pila . estáVacía ()) { var padre = pila . pop (); var derecha = padre . obtenerDerecha (); si ( derecha != null ) { pila . empujar ( derecha ); var hendidura = derecha . obtenerIzquierda (); mientras ( hendidura != null ) { pila . empujar ( hendidura ); hendidura = hendidura . obtenerIzquierda (); } } }                                 devolver resultado ; } }  

Reequilibrar

Definición: Reúne el conjunto de hojas L y reconstruye el árbol de abajo hacia arriba.

booleano estático isBalanced ( RopeLike r ) { val profundidad = r . profundidad (); si ( profundidad >= FIBONACCI_SEQUENCE . longitud - 2 ) { devuelve falso ; } devuelve FIBONACCI_SEQUENCE [ profundidad + 2 ] <= r . peso (); }                        reequilibrio estático de RopeLike ( RopeLike r ) { if ( ! isBalanced ( r )) { val leaves = Ropes . collectLeaves ( r ); return merge ( leaves , 0 , leaves . size ()); } return r ; }                  static RopeLike merge ( Lista < RopeLike > hojas ) { return merge ( hojas , 0 , hojas . tamaño ()); }        static RopeLike merge ( Lista < RopeLike > hojas , int inicio , int fin ) { int rango = fin - inicio ; si ( rango == 1 ) { devolver hojas . obtener ( inicio ); } si ( rango == 2 ) { devolver nuevo RopeLikeTree ( hojas . obtener ( inicio ), hojas . obtener ( inicio + 1 )); } int medio = inicio + ( rango / 2 ); devolver nuevo RopeLikeTree ( fusionar ( hojas , inicio , medio ), fusionar ( hojas , medio , fin )); }                                                  

Insertar

Definición: Insert(i, S’) : inserta la cadena S' comenzando en la posición i en la cadena s , para formar una nueva cadena C ₁ , ..., C _i , S' , C _{i + 1} , ..., C _m .

Complejidad temporal: ⁠ ⁠ ${\displaystyle O(\log N)}$ .

Esta operación se puede realizar mediante una Split()y dos Concat()operaciones. El costo es la suma de las tres.

public Rope insert ( int idx , CharSequence secuencia ) { if ( idx == 0 ) { return prepend ( secuencia ) ; } if ( idx == length ( ) ) { return append ( secuencia ) ; } val lhs = base.split ( idx ) ; return new Rope ( Soportes.concat ( lhs.fst.append ( secuencia ) , lhs.snd ) ) ; }​​                              

Índice

Figura 2.1: Ejemplo de búsqueda de índice en una cuerda.

Definición: Index(i) : devuelve el carácter en la posición i

Complejidad temporal: ⁠ ⁠ ${\displaystyle O(\log N)}$

Para recuperar el i -ésimo carácter, comenzamos una búsqueda recursiva desde el nodo raíz:

@Override public int indexOf ( char ch , int startIndex ) { if ( startIndex > peso ) { return right . indexOf ( ch , startIndex - peso ); } return left . indexOf ( ch , startIndex ); }                    

Por ejemplo, para encontrar el carácter en i=10en la Figura 2.1 que se muestra a la derecha, comience en el nodo raíz (A), encuentre que 22 es mayor que 10 y hay un hijo izquierdo, por lo que vaya al hijo izquierdo (B). 9 es menor que 10, por lo que reste 9 de 10 (dejando i=1) y vaya al hijo derecho (D). Luego, como 6 es mayor que 1 y hay un hijo izquierdo, vaya al hijo izquierdo (G). 2 es mayor que 1 y hay un hijo izquierdo, por lo que vaya al hijo izquierdo nuevamente (J). Finalmente, 2 es mayor que 1 pero no hay ningún hijo izquierdo, por lo que el carácter en el índice 1 de la cadena corta "na" (es decir, "n") es la respuesta. (Índice basado en 1)

Concat

Figura 2.2: Concatenación de dos cuerdas secundarias en una sola cuerda.

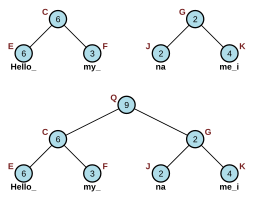
Definición: Concat(S1, S2) : concatenar dos cuerdas, S ₁ y S ₂ , en una sola cuerda.

Complejidad temporal: ⁠ ⁠ ${\displaystyle O(1)}$ (o ⁠ ⁠ ${\displaystyle O(\log N)}$ tiempo para calcular el peso de la raíz)

Se puede realizar una concatenación simplemente creando un nuevo nodo raíz con left = S1 y right = S2 , que es un tiempo constante. El peso del nodo padre se establece en la longitud del hijo izquierdo S ₁ , lo que tomaría ⁠ ⁠ tiempo, si el árbol está equilibrado. ${\displaystyle O(\log N)}$

Como la mayoría de las operaciones con cuerdas requieren árboles equilibrados, es posible que sea necesario volver a equilibrar el árbol después de la concatenación.

Dividir

Figura 2.3: División de una cuerda por la mitad.

Definición: Split (i, S) : divide la cadena S en dos nuevas cadenas S ₁ y S ₂ , S ₁ = C ₁ , ..., C _i y S ₂ = C _{i + 1} , ..., C _m .

Complejidad temporal: ⁠ ⁠ ${\displaystyle O(\log N)}$

Hay dos casos que deben abordarse:

1. El punto de división está al final de una cadena (es decir, después del último carácter de un nodo hoja)
2. El punto de división está en el medio de una cuerda.

El segundo caso se reduce al primero dividiendo la cadena en el punto de división para crear dos nuevos nodos hoja y luego creando un nuevo nodo que es el padre de las dos cadenas componentes.

Por ejemplo, para dividir la cuerda de 22 caracteres que se muestra en la Figura 2.3 en dos cuerdas de componentes iguales de longitud 11, consulte el duodécimo carácter para localizar el nodo K en el nivel inferior. Elimine el vínculo entre K y G. Vaya al padre de G y reste el peso de K del peso de D. Viaje hacia arriba en el árbol y elimine todos los vínculos de la derecha a los subárboles que cubran caracteres más allá de la posición 11, restando el peso de K de sus nodos padre (solo los nodos D y A , en este caso). Finalmente, construya los nodos recientemente huérfanos K y H concatenándolos entre sí y creando un nuevo padre P con un peso igual a la longitud del nodo izquierdo K.

Como la mayoría de las operaciones con cuerdas requieren árboles equilibrados, es posible que sea necesario volver a equilibrar el árbol después de partirlo.

public Pair < ​​RopeLike , RopeLike > split ( int índice ) { if ( índice < peso ) { val split = left . split ( índice ); return Pair . of ( rebalance ( split . fst ), rebalance ( new RopeLikeTree ( split . snd , right ))); } else if ( índice > peso ) { val split = right . split ( índice - peso ); return Pair . of ( rebalance ( new RopeLikeTree ( left , split . fst )), rebalance ( split . snd )); } else { return Pair . of ( left , right ); } }                                            

Borrar

Definición: Delete(i, j) : elimina la subcadena C _i , …, C _{i + j − 1} , de s para formar una nueva cadena C ₁ , …, C _{i − 1} , C _{i + j} , …, C _m .

Complejidad temporal: ⁠ ⁠ ${\displaystyle O(\log N)}$ .

Esta operación se puede realizar en dos Split()o en una sola Concat()operación. Primero, se divide la cuerda en tres, dividida por el i -ésimo y el i+j -ésimo carácter respectivamente, lo que extrae la cadena a eliminar en un nodo separado. Luego se concatenan los otros dos nodos.

@Override public RopeLike delete ( int start , int length ) { val lhs = split ( start ); val rhs = split ( start + length ); return rebalance ( new RopeLikeTree ( lhs . fst , rhs . snd )); }                    

Informe

Definición: Report(i, j) : genera la cadena C _i , …, C _{i + j − 1} .

Complejidad temporal: ⁠ ⁠ ${\displaystyle O(j+\log N)}$

Para informar la cadena C _i , …, C _{i + j − 1} , encuentre el nodo u que contiene C _i y weight(u) >= j, y luego recorra T comenzando en el nodo u . Genere C _i , …, C _{i + j − 1} haciendo un recorrido en orden de T comenzando en el nodo u .

Comparación con matrices monolíticas

Ventajas:

• Las cuerdas permiten una inserción y eliminación de texto mucho más rápida que las matrices de cadenas monolíticas, en las que las operaciones tienen una complejidad temporal de O(n).
• Las cuerdas no requieren O(n) memoria adicional cuando se opera sobre ellas (las matrices la necesitan para operaciones de copia).
• Las cuerdas no requieren grandes espacios de memoria contiguos.
• Si solo se utilizan versiones no destructivas de las operaciones, rope es una estructura de datos persistente . En el ejemplo del programa de edición de texto, esto permite admitir fácilmente varios niveles de deshacer .

Desventajas:

• Mayor uso general del espacio cuando no se está operando, principalmente para almacenar nodos principales. Existe una compensación entre qué parte de la memoria total es esa sobrecarga y cuánto tiempo se procesan los fragmentos de datos como cadenas. Las cadenas en las figuras de ejemplo anteriores son irrealmente cortas para las arquitecturas modernas. La sobrecarga siempre es O(n), pero la constante se puede hacer arbitrariamente pequeña.
• Aumento del tiempo para gestionar el almacenamiento adicional
• Mayor complejidad del código fuente; mayor riesgo de errores

Esta tabla compara los rasgos algorítmicos de las implementaciones de cadenas y cuerdas, no su velocidad bruta . Las cadenas basadas en matrices tienen una sobrecarga menor, por lo que (por ejemplo) las operaciones de concatenación y división son más rápidas en conjuntos de datos pequeños. Sin embargo, cuando se utilizan cadenas basadas en matrices para cadenas más largas, la complejidad temporal y el uso de memoria para insertar y eliminar caracteres se vuelven inaceptablemente grandes. Por el contrario, una estructura de datos de cuerdas tiene un rendimiento estable independientemente del tamaño de los datos. Además, la complejidad espacial de las cuerdas y las matrices es O(n). En resumen, las cuerdas son preferibles cuando los datos son grandes y se modifican con frecuencia.

Véase también

• El entorno de programación Cedar , que utilizó cuerdas "casi desde sus inicios" ^[1]
• La enfilada del Modelo T , una estructura de datos similar de principios de la década de 1970
• Buffer de espacio , una estructura de datos comúnmente utilizada en editores de texto que permite operaciones de inserción y eliminación eficientes agrupadas cerca de la misma ubicación
• Tabla de piezas , otra estructura de datos comúnmente utilizada en editores de texto

Referencias

1. Boehm, Hans-J; Atkinson, Russ; Plass, Michael (diciembre de 1995). «Cuerdas: una alternativa a las cuerdas» ( PDF ) . Software: práctica y experiencia . 25 (12). Nueva York, NY, EE. UU.: John Wiley & Sons, Inc.: 1315–1330. doi :10.1002/spe.4380251203. Archivado desde el original el 8 de marzo de 2020.
2. "Descripción general de la implementación de cuerdas". www.sgi.com . Archivado desde el original el 19 de diciembre de 2017 . Consultado el 1 de marzo de 2017 .

Enlaces externos

• Implementación de cuerdas "absl::Cord" dentro de la biblioteca Abseil
• Implementación de cuerdas "C cords" dentro de la biblioteca del Recolector de Basura Boehm
• Especificación SGI C++ para cuerdas (compatible con STLPort y libstdc++)
• Cuerdas para C#
• Cuerdas para Common Lisp
• Cuerdas para Java
• Cuerdas tipo cuerda para Java
• Cuerdas para JavaScript
• Cuerdas para el limbo
• Cuerdas para Nim
• Cuerdas para OCaml
• piropos para Python
• Cuerdas para Smalltalk
• Cuerda SwiftRope para Swift
• "Ropey" para Rust