El pipeline de gráficos por computadora , también conocido como pipeline de renderizado o pipeline de gráficos , es un marco dentro de los gráficos por computadora que describe los procedimientos necesarios para transformar una escena tridimensional (3D) en una representación bidimensional (2D) en una pantalla. [1] Una vez que se genera un modelo 3D, el pipeline de gráficos convierte el modelo en un formato visualmente perceptible en la pantalla de la computadora. [2] Debido a la dependencia de software específico , configuraciones de hardware y atributos de visualización deseados, no existe un pipeline de gráficos de aplicación universal. Sin embargo, las interfaces de programación de aplicaciones gráficas (API), como Direct3D , OpenGL y Vulkan, se desarrollaron para estandarizar procedimientos comunes y supervisar el pipeline de gráficos de un acelerador de hardware determinado. Estas API proporcionan una capa de abstracción sobre el hardware subyacente, lo que libera a los programadores de la necesidad de escribir código dirigido explícitamente a varios aceleradores de hardware de gráficos como AMD , Intel , Nvidia y otros.
El modelo de pipeline de gráficos se utiliza habitualmente en la renderización en tiempo real. A menudo, la mayoría de los pasos de pipeline se implementan en hardware, lo que permite realizar optimizaciones especiales . El término "pipeline" se utiliza en un sentido similar para el pipeline en procesadores : los pasos individuales del pipeline se ejecutan en paralelo siempre que cada paso tenga lo que necesita.
El término "canalización 3D" hace referencia generalmente a la forma más común de renderización tridimensional por ordenador denominada renderización poligonal 3D [ cita requerida ] , distinta del trazado de rayos y del raycasting . En el raycasting, un rayo se origina en el punto en el que se encuentra la cámara y, si ese rayo incide en una superficie, se calcula el color y la iluminación del punto de la superficie en el que incide el rayo. En la renderización poligonal 3D ocurre lo contrario: se calcula el área que se le asigna a la cámara y, a continuación, se crean rayos desde cada parte de cada superficie que se le asigna a la cámara y se trazan hasta llegar a la cámara. [3]
Una canalización de gráficos se puede dividir en tres partes principales: Aplicación, Geometría y Rasterización. [4]
El paso de aplicación lo ejecuta el software en el procesador principal ( CPU ). Durante el paso de aplicación, se realizan cambios en la escena según sea necesario, por ejemplo, mediante la interacción del usuario con dispositivos de entrada o durante una animación. La nueva escena con todos sus elementos primitivos , generalmente triángulos, líneas y puntos, se pasa luego al siguiente paso del proceso.
Ejemplos de tareas que se realizan normalmente en el paso de aplicación son la detección de colisiones , la animación, la transformación y las técnicas de aceleración que utilizan esquemas de subdivisión espacial como Quadtrees u Octrees . Estos también se utilizan para reducir la cantidad de memoria principal necesaria en un momento dado. El "mundo" de un juego de ordenador moderno es mucho más grande de lo que podría caber en la memoria a la vez.
El paso de geometría (con la secuencia de comandos Geometry ), que es responsable de la mayoría de las operaciones con polígonos y sus vértices (con la secuencia de comandos Vertex ), se puede dividir en las siguientes cinco tareas. Depende de la implementación particular cómo se organizan estas tareas como pasos de secuencia de comandos paralelos reales.
Un vértice (plural: vértices) es un punto en el mundo. Se utilizan muchos puntos para unir las superficies. En casos especiales, las nubes de puntos se dibujan directamente, pero esto sigue siendo la excepción.
El triángulo es la primitiva geométrica más común en los gráficos por ordenador. Se define por sus tres vértices y un vector normal (el vector normal sirve para indicar la cara frontal del triángulo y es un vector que es perpendicular a la superficie). El triángulo puede estar provisto de un color o de una textura (una imagen "pegada" sobre él). Los triángulos son preferibles a los rectángulos porque sus tres puntos siempre existen en un único plano .
El sistema de coordenadas del mundo es el sistema de coordenadas en el que se crea el mundo virtual. Debe cumplir algunas condiciones para que las siguientes operaciones matemáticas sean fácilmente aplicables:
La definición de la unidad del sistema de coordenadas queda a criterio del desarrollador. Por tanto, depende de la aplicación si el vector unitario del sistema corresponde en realidad a un metro o a un Ångström .
Los objetos contenidos en la escena (casas, árboles, coches) suelen diseñarse en su sistema de coordenadas de objeto (también llamado sistema de coordenadas del modelo o sistema de coordenadas local) por razones de simplificación del modelado. Para asignar a estos objetos las coordenadas del sistema de coordenadas mundial o del sistema de coordenadas global de toda la escena, las coordenadas del objeto se transforman mediante traslación, rotación o escalado. Esto se hace multiplicando las matrices de transformación correspondientes . Además, se pueden formar varias copias transformadas de forma diferente a partir de un objeto, por ejemplo, un bosque a partir de un árbol; esta técnica se denomina instanciación.
En primer lugar, necesitamos tres matrices de rotación , es decir, una para cada uno de los tres ejes de la aeronave (eje vertical, eje transversal, eje longitudinal).
También utilizamos una matriz de traducción que mueve la aeronave al punto deseado en nuestro mundo: .
Ahora podríamos calcular la posición de los vértices del avión en coordenadas del mundo multiplicando cada punto sucesivamente por estas cuatro matrices. Dado que la multiplicación de una matriz por un vector es bastante costosa (requiere mucho tiempo), normalmente se toma otro camino y primero se multiplican las cuatro matrices entre sí. La multiplicación de dos matrices es aún más costosa, pero debe ejecutarse solo una vez para todo el objeto. Las multiplicaciones y son equivalentes. A continuación, la matriz resultante podría aplicarse a los vértices. Sin embargo, en la práctica, la multiplicación con los vértices aún no se aplica, sino que primero se determinan las matrices de la cámara (ver a continuación).
El orden en el que se aplican las matrices es importante porque la multiplicación de matrices no es conmutativa . Esto también se aplica a las tres rotaciones, lo que se puede demostrar con un ejemplo: el punto (1, 0, 0) se encuentra en el eje X, si uno lo gira primero 90° alrededor del eje X y luego alrededor del eje Y, termina en el eje Z (la rotación alrededor del eje X no afecta a un punto que está en el eje). Si, por otro lado, uno gira primero alrededor del eje Y y luego alrededor del eje X, el punto resultante se encuentra en el eje Y. La secuencia en sí es arbitraria siempre que sea siempre la misma. La secuencia con x, luego y, luego z (balanceo, cabeceo, rumbo) es a menudo la más intuitiva porque la rotación hace que la dirección de la brújula coincida con la dirección del "morro".
También existen dos convenciones para definir estas matrices, dependiendo de si se desea trabajar con vectores columna o vectores fila. Las diferentes bibliotecas gráficas tienen diferentes preferencias en este sentido. OpenGL prefiere los vectores columna, mientras que DirectX prefiere los vectores fila. La decisión determina desde qué lado se multiplicarán los vectores de puntos por las matrices de transformación. Para los vectores columna, la multiplicación se realiza desde la derecha, es decir , donde v out y v in son vectores columna de 4x1. La concatenación de las matrices también se realiza de derecha a izquierda, es decir, por ejemplo , cuando primero se rota y luego se desplaza.
En el caso de los vectores fila, esto funciona exactamente al revés. La multiplicación ahora se realiza desde la izquierda como en los vectores fila 1x4 y la concatenación se produce cuando también primero giramos y luego movemos. Las matrices mostradas arriba son válidas para el segundo caso, mientras que las de los vectores columna se transponen. Se aplica la regla [5] , que para la multiplicación con vectores significa que se puede cambiar el orden de multiplicación transponiendo la matriz.
En el encadenamiento de matrices, cada transformación define un nuevo sistema de coordenadas, lo que permite extensiones flexibles. Por ejemplo, la hélice de un avión, modelada por separado, se puede unir a la nariz del avión mediante una traslación, que solo cambia del modelo al sistema de coordenadas de la hélice. Para renderizar el avión, primero se calcula su matriz de transformación para transformar los puntos, seguido de la multiplicación de la matriz del modelo de la hélice por la matriz del avión para los puntos de la hélice. Esta matriz calculada se conoce como la "matriz mundial", esencial para cada objeto en la escena antes de la renderización. La aplicación puede luego alterar dinámicamente estas matrices, como actualizar la posición del avión con cada cuadro en función de la velocidad.
La matriz calculada de esta manera también se denomina matriz mundial . Debe determinarse para cada objeto del mundo antes de la renderización. La aplicación puede introducir aquí cambios, por ejemplo, cambiando la posición del avión en función de la velocidad después de cada fotograma.
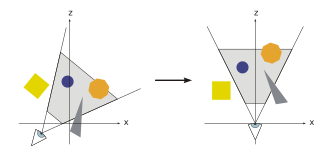
Además de los objetos, la escena también define una cámara virtual o visor que indica la posición y la dirección de la vista con respecto a la cual se representa la escena. La escena se transforma de modo que la cámara esté en el origen mirando a lo largo del eje Z. El sistema de coordenadas resultante se denomina sistema de coordenadas de la cámara y la transformación se denomina transformación de la cámara o transformación de la vista .
Zaxis = normal(cameraPosition - cameraTarget)Xaxis = normal(cross(cameraUpVector, Zaxis))Yaxis = cross(Zaxis, Xaxis )El paso de proyección 3D transforma el volumen de la vista en un cubo con las coordenadas de los puntos de esquina (-1, -1, 0) y (1, 1, 1); ocasionalmente también se utilizan otros volúmenes de destino. Este paso se llama proyección , aunque transforma un volumen en otro volumen, ya que las coordenadas Z resultantes no se almacenan en la imagen, sino que solo se utilizan en el almacenamiento en búfer Z en el paso de rasterización posterior. En una ilustración en perspectiva , se utiliza una proyección central . Para limitar el número de objetos mostrados, se utilizan dos planos de recorte adicionales; el volumen visual es, por lo tanto, una pirámide truncada ( truncado ). La proyección paralela u ortogonal se utiliza, por ejemplo, para representaciones técnicas porque tiene la ventaja de que todos los paralelos en el espacio de objetos también son paralelos en el espacio de la imagen, y las superficies y los volúmenes tienen el mismo tamaño independientemente de la distancia desde el espectador. Los mapas utilizan, por ejemplo, una proyección ortogonal (la llamada ortofoto ), pero las imágenes oblicuas de un paisaje no se pueden utilizar de esta manera: aunque técnicamente se pueden reproducir, parecen tan distorsionadas que no podemos hacer uso de ellas. La fórmula para calcular una matriz de proyección en perspectiva es:
Las razones por las que aquí se deben indicar la distancia más pequeña y la más grande son, por un lado, que esta distancia se divide para alcanzar la escala de la escena (los objetos más distantes son más pequeños en una imagen en perspectiva que los objetos cercanos), y por otro lado para escalar los valores Z al rango 0..1, para llenar el búfer Z. Este búfer a menudo tiene una resolución de solo 16 bits, por lo que los valores de cerca y lejos deben elegirse con cuidado. Una diferencia demasiado grande entre el valor de cerca y el de lejos conduce a lo que se denomina Z-fighting debido a la baja resolución del búfer Z. También se puede ver en la fórmula que el valor de cerca no puede ser 0 porque este punto es el punto de enfoque de la proyección. No hay imagen en este punto.
Para completar, la fórmula para la proyección paralela (proyección ortogonal):
Por razones de eficiencia, la cámara y la matriz de proyección se combinan normalmente en una matriz de transformación, de modo que se omite el sistema de coordenadas de la cámara. La matriz resultante suele ser la misma para una sola imagen, mientras que la matriz del mundo se ve diferente para cada objeto. Por lo tanto, en la práctica, la vista y la proyección se calculan previamente de modo que solo se debe adaptar la matriz del mundo durante la visualización. Sin embargo, son posibles transformaciones más complejas, como la combinación de vértices. También se pueden ejecutar sombreadores de geometría libremente programables que modifican la geometría.
En el paso de renderizado propiamente dicho, se calcula la matriz del mundo * matriz de la cámara * matriz de proyección y, finalmente, se aplica a cada punto. De este modo, los puntos de todos los objetos se transfieren directamente al sistema de coordenadas de la pantalla (al menos casi, el rango de valores de los ejes sigue siendo -1..1 para el rango visible, consulte la sección "Transformación de ventana-ventana gráfica").
A menudo, una escena contiene fuentes de luz colocadas en diferentes posiciones para que la iluminación de los objetos parezca más realista. En este caso, se calcula un factor de ganancia para la textura para cada vértice en función de las fuentes de luz y las propiedades del material asociadas con el triángulo correspondiente. En el paso posterior de rasterización, los valores de los vértices de un triángulo se interpolan sobre su superficie. Se aplica una iluminación general (luz ambiental) a todas las superficies. Es el brillo difuso y, por lo tanto, independiente de la dirección de la escena. El sol es una fuente de luz dirigida, que se puede suponer que está infinitamente lejos. La iluminación realizada por el sol sobre una superficie se determina formando el producto escalar del vector direccional del sol y el vector normal de la superficie. Si el valor es negativo, la superficie está orientada hacia el sol.

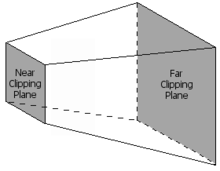
Solo es necesario rasterizar (dibujar) los primitivos que se encuentran dentro del volumen visual. Este volumen visual se define como el interior de un tronco de cono , una forma en forma de pirámide con la parte superior cortada. Los primitivos que están completamente fuera del volumen visual se descartan; esto se denomina eliminación de troncos de cono . En teoría, se pueden ejecutar otros métodos de eliminación, como la eliminación de caras posteriores, que reduce la cantidad de primitivos a considerar, en cualquier paso del proceso de gráficos. Los primitivos que solo están parcialmente dentro del cubo se deben recortar contra el cubo. La ventaja del paso de proyección anterior es que el recorte siempre se realiza contra el mismo cubo. Solo los primitivos (posiblemente recortados) que se encuentran dentro del volumen visual se envían al paso final.

Para enviar la imagen a cualquier área de destino (ventana gráfica) de la pantalla, se debe aplicar otra transformación, la transformación Ventana-Vista gráfica . Se trata de un desplazamiento, seguido de un escalado. Las coordenadas resultantes son las coordenadas del dispositivo de salida. La ventana gráfica contiene 6 valores: la altura y el ancho de la ventana en píxeles, la esquina superior izquierda de la ventana en coordenadas de ventana (normalmente 0, 0) y los valores mínimo y máximo de Z (normalmente 0 y 1).
En el hardware moderno, la mayoría de los pasos de cálculo de la geometría se realizan en el vertex shader . Este, en principio, es libremente programable, pero generalmente realiza al menos la transformación de los puntos y el cálculo de la iluminación. Para la interfaz de programación DirectX, es necesario el uso de un vertex shader personalizado a partir de la versión 10, mientras que las versiones anteriores aún cuentan con un shader estándar.
El paso de rasterización es el paso final antes de la secuencia de sombreado de fragmentos con la que se rasterizan todos los primitivos . En el paso de rasterización, se crean fragmentos discretos a partir de primitivos continuos.
En esta etapa del pipeline de gráficos, los puntos de la cuadrícula también se denominan fragmentos, para que sean más distintivos. Cada fragmento corresponde a un píxel en el búfer de cuadros y este corresponde a un píxel de la pantalla. Estos pueden ser coloreados (y posiblemente iluminados). Además, es necesario determinar el fragmento visible, más cercano al observador, en el caso de polígonos superpuestos. Por lo general, se utiliza un búfer Z para esta determinación de la denominada superficie oculta . El color de un fragmento depende de la iluminación, la textura y otras propiedades del material de la primitiva visible y, a menudo, se interpola utilizando las propiedades del vértice del triángulo. Cuando está disponible, se ejecuta un sombreador de fragmentos (también llamado Pixel Shader ) en el paso de rasterización para cada fragmento del objeto. Si un fragmento es visible, ahora se puede mezclar con valores de color ya existentes en la imagen si se utiliza transparencia o muestreo múltiple. En este paso, uno o más fragmentos se convierten en un píxel.
Para evitar que el usuario vea la rasterización gradual de las primitivas, se realiza un doble buffering. La rasterización se lleva a cabo en un área de memoria especial. Una vez que la imagen ha sido completamente rasterizada, se copia al área visible de la memoria de imágenes.
Todas las matrices utilizadas son no singulares y, por lo tanto, invertibles. Dado que la multiplicación de dos matrices no singulares crea otra matriz no singular, la matriz de transformación completa también es invertible. La inversa es necesaria para recalcular las coordenadas del mundo a partir de las coordenadas de la pantalla; por ejemplo, para determinar a partir de la posición del puntero del ratón el objeto en el que se ha hecho clic. Sin embargo, dado que la pantalla y el ratón tienen solo dos dimensiones, la tercera es desconocida. Por lo tanto, se proyecta un rayo en la posición del cursor hacia el mundo y luego se determina la intersección de este rayo con los polígonos del mundo.
Las tarjetas gráficas clásicas todavía están relativamente cerca del pipeline de gráficos. A medida que aumentaban las exigencias sobre la GPU , se fueron eliminando gradualmente las restricciones para crear más flexibilidad. Las tarjetas gráficas modernas utilizan un pipeline controlado por sombreadores y programable libremente, que permite el acceso directo a los pasos de procesamiento individuales. Para aliviar al procesador principal, se han trasladado pasos de procesamiento adicionales al pipeline y a la GPU.
Las unidades de sombreado más importantes son los sombreadores de vértices , los sombreadores de geometría y los sombreadores de píxeles.
Se ha introducido el sombreador unificado para aprovechar al máximo todas las unidades. Esto proporciona un único y gran conjunto de unidades de sombreadores. Según sea necesario, el conjunto se divide en diferentes grupos de sombreadores. Por lo tanto, ya no resulta útil una separación estricta entre los tipos de sombreadores.
También es posible utilizar un denominado "compute-shader" para realizar cualquier cálculo a partir de la visualización de un gráfico en la GPU. La ventaja es que se ejecutan de forma muy paralela, pero existen limitaciones. Estos cálculos universales también se denominan computación de propósito general en unidades de procesamiento gráfico o GPGPU , por sus siglas en inglés.
Los sombreadores de malla son una incorporación reciente que apunta a superar los cuellos de botella del diseño fijo de la tubería de geometría. [6]