La rectificación de imágenes es un proceso de transformación que se utiliza para proyectar imágenes en un plano de imagen común. Este proceso tiene varios grados de libertad y existen muchas estrategias para transformar imágenes en el plano común. La rectificación de imágenes se utiliza en la visión estereoscópica por computadora para simplificar el problema de encontrar puntos coincidentes entre imágenes (es decir, el problema de correspondencia ) y en los sistemas de información geográfica (SIG) para fusionar imágenes tomadas desde múltiples perspectivas en un sistema de coordenadas de mapa común.
La visión estereoscópica por computadora toma dos o más imágenes con posiciones relativas conocidas de la cámara que muestran un objeto desde diferentes puntos de vista. Para cada píxel, luego determina la profundidad del punto de escena correspondiente (es decir, la distancia desde la cámara) al encontrar primero píxeles coincidentes (es decir, píxeles que muestran el mismo punto de escena) en las otras imágenes y luego aplicar triangulación a las coincidencias encontradas para determinar su profundidad. Encontrar coincidencias en la visión estereoscópica está restringido por la geometría epipolar : la coincidencia de cada píxel en otra imagen solo se puede encontrar en una línea llamada línea epipolar. Si dos imágenes son coplanares, es decir, se tomaron de manera que la cámara derecha solo está desplazada horizontalmente en comparación con la cámara izquierda (no se mueve hacia el objeto ni se rota), entonces la línea epipolar de cada píxel es horizontal y está en la misma posición vertical que ese píxel. Sin embargo, en configuraciones generales (la cámara se mueve hacia el objeto o rota) las líneas epipolares están inclinadas. La rectificación de imágenes deforma ambas imágenes de modo que parezcan tomadas con un desplazamiento horizontal únicamente y, como consecuencia, todas las líneas epipolares son horizontales, lo que simplifica ligeramente el proceso de comparación estereoscópica. Sin embargo, cabe señalar que la rectificación no cambia fundamentalmente el proceso de comparación estereoscópica: busca líneas, líneas inclinadas antes y líneas horizontales después de la rectificación.
La rectificación de imagen también es una alternativa equivalente (y más utilizada [1] ) a la coplanaridad perfecta de la cámara. Incluso con equipos de alta precisión, la rectificación de imagen se suele realizar porque puede resultar poco práctico mantener una coplanaridad perfecta entre cámaras.
La rectificación de imágenes sólo se puede realizar con dos imágenes a la vez y la rectificación simultánea de más de dos imágenes generalmente es imposible. [2]
Si las imágenes que se van a rectificar se toman de pares de cámaras sin distorsión geométrica , este cálculo se puede realizar fácilmente con una transformación lineal . La rotación X e Y coloca las imágenes en el mismo plano, el escalado hace que los marcos de la imagen tengan el mismo tamaño y la rotación Z y los ajustes de inclinación hacen que las filas de píxeles de la imagen se alineen directamente [ cita requerida ] . Es necesario conocer la alineación rígida de las cámaras (mediante calibración) y la transformación utiliza los coeficientes de calibración. [3]
Al realizar la transformación, si las cámaras mismas están calibradas para parámetros internos, una matriz esencial proporciona la relación entre las cámaras. El caso más general (sin calibración de cámaras) está representado por la matriz fundamental . Si no se conoce la matriz fundamental, es necesario encontrar correspondencias puntuales preliminares entre imágenes estereoscópicas para facilitar su extracción. [3]
Existen tres categorías principales de algoritmos de rectificación de imágenes: rectificación planar, [4] rectificación cilíndrica [1] y rectificación polar. [5] [6] [7]
Todas las imágenes rectificadas satisfacen las dos propiedades siguientes: [8]
Para transformar el par de imágenes original en un par de imágenes rectificado, es necesario encontrar una transformación proyectiva H . Se imponen restricciones a H para satisfacer las dos propiedades anteriores. Por ejemplo, restringir que las líneas epipolares sean paralelas al eje horizontal significa que los epipolos deben mapearse al punto infinito [1,0,0] T en coordenadas homogéneas . Incluso con estas restricciones, H todavía tiene cuatro grados de libertad. [9] También es necesario encontrar un H' coincidente para rectificar la segunda imagen de un par de imágenes. Las malas elecciones de H y H' pueden dar como resultado imágenes rectificadas que cambian drásticamente en escala o están severamente distorsionadas.
Existen muchas estrategias diferentes para elegir una transformación proyectiva H para cada imagen de entre todas las soluciones posibles. Un método avanzado consiste en minimizar la disparidad o la diferencia de mínimos cuadrados de los puntos correspondientes en el eje horizontal del par de imágenes rectificadas. [9] Otro método consiste en separar H en una transformación proyectiva especializada, una transformación de similitud y una transformación de corte para minimizar la distorsión de la imagen. [8] Un método simple consiste en rotar ambas imágenes para que se vean perpendiculares a la línea que une sus centros ópticos colectivos, torcer los ejes ópticos de modo que el eje horizontal de cada imagen apunte en la dirección del centro óptico de la otra imagen y, finalmente, escalar la imagen más pequeña para que coincida con la correspondencia línea a línea. [2] Este proceso se demuestra en el siguiente ejemplo.
Nuestro modelo para este ejemplo se basa en un par de imágenes que observan un punto 3D P , que corresponde a p y p' en las coordenadas de píxeles de cada imagen. O y O' representan los centros ópticos de cada cámara, con matrices de cámara conocidas y (asumimos que el origen mundial está en la primera cámara). Describiremos y representaremos brevemente los resultados de un enfoque simple para encontrar una transformación proyectiva H y H' que rectifique el par de imágenes de la escena de ejemplo.
Primero, calculamos los epípolos, e y e' en cada imagen:
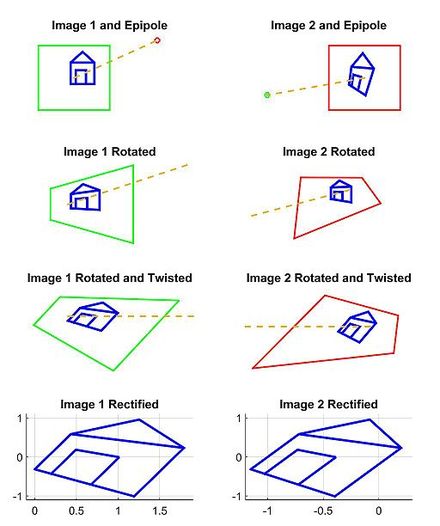
En segundo lugar, encontramos una transformación proyectiva H 1 que rota nuestra primera imagen para que sea paralela a la línea base que conecta O y O' (fila 2, columna 1 del conjunto de imágenes 2D). Esta rotación se puede encontrar utilizando el producto vectorial entre los ejes ópticos original y deseado. [2] A continuación, encontramos la transformación proyectiva H 2 que toma la imagen rotada y la tuerce de modo que el eje horizontal se alinee con la línea base. Si se calcula correctamente, esta segunda transformación debería mapear la e al infinito en el eje x (fila 3, columna 1 del conjunto de imágenes 2D). Finalmente, defina como la transformación proyectiva para rectificar la primera imagen.
En tercer lugar, mediante una operación equivalente, podemos encontrar H' para rectificar la segunda imagen (columna 2 del conjunto de imágenes 2D). Nótese que H' 1 debe rotar el eje óptico de la segunda imagen para que sea paralelo al eje óptico transformado de la primera imagen. Una estrategia es elegir un plano paralelo a la línea donde se intersecan los dos ejes ópticos originales para minimizar la distorsión del proceso de reproyección. [10] En este ejemplo, simplemente definimos H' utilizando la matriz de rotación R y la transformación proyectiva inicial H como .
Finalmente, escalamos ambas imágenes a la misma resolución aproximada y alineamos los epípolos ahora horizontales para facilitar el escaneo horizontal en busca de correspondencias (fila 4 del conjunto de imágenes 2D).
Tenga en cuenta que es posible realizar este y otros algoritmos similares sin tener las matrices de parámetros de la cámara M y M' . Todo lo que se requiere es un conjunto de siete o más correspondencias imagen a imagen para calcular las matrices fundamentales y los epípolos. [9]
La rectificación de imágenes en SIG convierte las imágenes a un sistema de coordenadas de mapa estándar. Esto se hace haciendo coincidir los puntos de control terrestre (GCP) en el sistema de mapeo con los puntos en la imagen. Estos GCP calculan las transformaciones de imagen necesarias. [11]
Las principales dificultades en el proceso ocurren
Los mapas que se utilizan con imágenes rectificadas no son topográficos. Sin embargo, las imágenes que se utilizan pueden contener distorsiones del terreno. La ortorectificación de imágenes elimina además estos efectos. [11]
La rectificación de imágenes es una función estándar disponible con los paquetes de software SIG.
![{\displaystyle M=K[I~0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36bab3ec4fb0bb080e213c2ed255b77a3783af3b)
![{\displaystyle M'=K'[R~T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b49a26dca801d091e45d483e46eb0a17a883c28)
![{\displaystyle e=M{\begin{bmatrix}O'\\1\end{bmatrix}}=M{\begin{bmatrix}-R^{T}T\\1\end{bmatrix}}=K[I~0]{\begin{bmatrix}-R^{T}T\\1\end{bmatrix}}=-KR^{T}T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27b3eb1954bb32452aaee6d928968474f9e3b358)
![{\displaystyle e'=M'{\begin{bmatrix}O\\1\end{bmatrix}}=M'{\begin{bmatrix}0\\1\end{bmatrix}}=K'[R~T]{\begin{bmatrix}0\\1\end{bmatrix}}=K'T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2f0d667c156022e71390855e68b60621c65cead)
