La reciprocidad en las redes eléctricas es una propiedad de un circuito que relaciona voltajes y corrientes en dos puntos. El teorema de reciprocidad establece que la corriente en un punto de un circuito debida a un voltaje en un segundo punto es la misma que la corriente en el segundo punto debida al mismo voltaje en el primero. El teorema de reciprocidad es válido para casi todas las redes pasivas . El teorema de reciprocidad es una característica de un principio más general de reciprocidad en electromagnetismo .
Si una corriente , , inyectada en el puerto A produce un voltaje , , en el puerto B y la inyectada en el puerto B produce en el puerto A, entonces se dice que la red es recíproca. De manera equivalente, la reciprocidad se puede definir por la situación dual; aplicar voltaje, , en el puerto A produciendo corriente en el puerto B y en el puerto B produciendo corriente en el puerto A. [1] En general, las redes pasivas son recíprocas. Cualquier red que consista completamente en capacitancias ideales , inductancias (incluidas las inductancias mutuas ) y resistencias , es decir, elementos que son lineales y bilaterales, será recíproca. [2] Sin embargo, existen componentes pasivos que no son recíprocos. Es probable que cualquier componente que contenga material ferromagnético no sea recíproco. Los ejemplos de componentes pasivos diseñados deliberadamente para ser no recíprocos incluyen circuladores y aisladores . [3]
La función de transferencia de una red recíproca tiene la propiedad de ser simétrica respecto de la diagonal principal si se expresa en términos de una matriz de parámetros z , parámetros y o parámetros s . Una matriz no simétrica implica una red no recíproca. Una matriz simétrica no implica una red simétrica . [4]
En algunas parametrizaciones de redes, la matriz representativa no es simétrica para redes recíprocas. Ejemplos comunes son los parámetros h y los parámetros ABCD , pero todos tienen alguna otra condición de reciprocidad que se puede calcular a partir de los parámetros. Para los parámetros h, la condición es y para los parámetros ABCD es . Estas representaciones mezclan voltajes y corrientes en el mismo vector de columna y, por lo tanto, ni siquiera tienen unidades coincidentes en los elementos transpuestos . [5]
Un ejemplo de reciprocidad se puede demostrar utilizando un atenuador resistivo asimétrico . Se elige una red asimétrica como ejemplo porque una red simétrica es evidentemente recíproca.
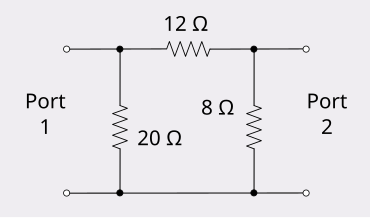
Inyectar 6 amperios en el puerto 1 de esta red produce 24 voltios en el puerto 2.
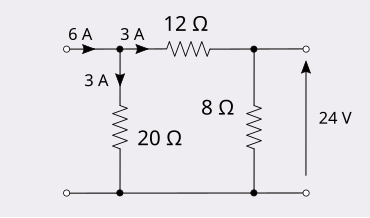
Inyectar 6 amperios en el puerto 2 produce 24 voltios en el puerto 1.
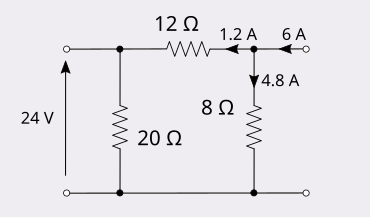
Por lo tanto, la red es recíproca. En este ejemplo, el puerto que no está inyectando corriente se deja en circuito abierto. Esto se debe a que un generador de corriente que aplica corriente cero es un circuito abierto. Si, por el contrario, se quisiera aplicar voltajes y medir la corriente resultante, entonces el puerto al que no se aplica el voltaje se pondría en cortocircuito. Esto se debe a que un generador de voltaje que aplica cero voltios es un cortocircuito.
La reciprocidad de las redes eléctricas es un caso especial de reciprocidad de Lorentz , pero también se puede demostrar de forma más directa a partir de teoremas de redes. Esta prueba muestra la reciprocidad para una red de dos nodos en términos de su matriz de admitancia , y luego muestra la reciprocidad para una red con un número arbitrario de nodos mediante un argumento de inducción . Una red lineal se puede representar como un conjunto de ecuaciones lineales mediante análisis nodal . Para una red que consta de n +1 nodos (uno de ellos un nodo de referencia) donde, en general, se conecta una admitancia entre cada par de nodos y donde se inyecta una corriente en cada nodo (proporcionada por una fuente de corriente ideal conectada entre el nodo y el nodo de referencia), estas ecuaciones se pueden expresar en forma de una matriz de admitancia, [6]
dónde
Esta representación corresponde a la obtenida mediante el análisis nodal . Si además requerimos que la red esté formada por elementos pasivos bilaterales, entonces
ya que la admitancia conectada entre los nodos j y k es el mismo elemento que la admitancia conectada entre los nodos k y j . Por lo tanto, la matriz es simétrica. [7] Para el caso en que la matriz se reduce a,
De lo cual se desprende que,
Pero desde entonces,
que es sinónimo de la condición de reciprocidad. En palabras, la relación entre la corriente en un puerto y el voltaje en otro es la misma si los puertos que se activan y se miden están intercambiados. Por lo tanto, se demuestra la reciprocidad para el caso de . [8]
Para el caso de una matriz de tamaño arbitrario, el orden de la matriz se puede reducir mediante la eliminación de nodos . Después de eliminar el nodo s , la nueva matriz de admitancia tendrá la forma,
Se puede observar que esta nueva matriz también es simétrica. Se pueden seguir eliminando nodos de esta manera hasta que solo quede una matriz simétrica de 2×2 que involucre a los dos nodos de interés. Dado que esta matriz es simétrica, se demuestra que la reciprocidad se aplica a una matriz de tamaño arbitrario cuando un nodo es impulsado por una tensión y una corriente medidas en otro. Un proceso similar que utiliza la matriz de impedancia del análisis de malla demuestra la reciprocidad cuando un nodo es impulsado por una corriente y se mide la tensión en otro. [9]