Pruebas grupales

Procedimiento que divide la tarea de identificar ciertos objetos en pruebas sobre grupos de elementos.

Ejemplo del problema de la bombilla, en el que se busca una bombilla rota entre seis bombillas. En este caso, las tres primeras están conectadas a una fuente de alimentación y se encienden (A). Esto indica que la bombilla rota debe ser una de las tres últimas (B). Si, en cambio, las bombillas no se encienden, se podría estar seguro de que la bombilla rota se encuentra entre las tres primeras. Si se continúa con este procedimiento, se puede localizar la bombilla rota en no más de tres pruebas, en comparación con un máximo de seis pruebas si se comprueban las bombillas individualmente.

En estadística y matemática combinatoria , la prueba de grupo es cualquier procedimiento que divide la tarea de identificar ciertos objetos en pruebas sobre grupos de elementos, en lugar de sobre elementos individuales. Estudiada por primera vez por Robert Dorfman en 1943, la prueba de grupo es un campo relativamente nuevo de las matemáticas aplicadas que se puede aplicar a una amplia gama de aplicaciones prácticas y es un área activa de investigación en la actualidad.

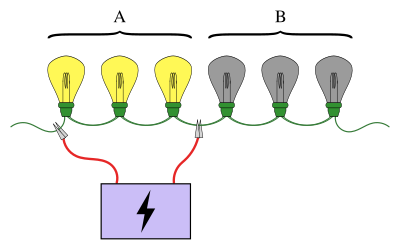
Un ejemplo conocido de prueba en grupo es el de una serie de bombillas conectadas en serie, en la que se sabe que una de ellas está rota. El objetivo es encontrar la bombilla rota utilizando el menor número de pruebas (una prueba es cuando algunas de las bombillas están conectadas a una fuente de alimentación). Un enfoque sencillo es probar cada bombilla individualmente. Sin embargo, cuando hay una gran cantidad de bombillas, sería mucho más eficiente agruparlas. Por ejemplo, al conectar la primera mitad de las bombillas a la vez, se puede determinar en qué mitad está la bombilla rota, descartando la mitad de las bombillas en una sola prueba.

Los esquemas para llevar a cabo pruebas grupales pueden ser simples o complejos y las pruebas involucradas en cada etapa pueden ser diferentes. Los esquemas en los que las pruebas para la siguiente etapa dependen de los resultados de las etapas anteriores se denominan procedimientos adaptativos , mientras que los esquemas diseñados de manera que todas las pruebas se conocen de antemano se denominan procedimientos no adaptativos . La estructura del esquema de las pruebas involucradas en un procedimiento no adaptativo se conoce como diseño de agrupamiento .

Las pruebas grupales tienen muchas aplicaciones, entre ellas la estadística, la biología, la informática, la medicina, la ingeniería y la ciberseguridad. El interés moderno por estos sistemas de pruebas se ha reavivado con el Proyecto Genoma Humano . ^[1]

Descripción básica y términos

A diferencia de muchas áreas de las matemáticas, los orígenes de las pruebas grupales se remontan a un solo informe ^[2] escrito por una sola persona: Robert Dorfman . ^[3] La motivación surgió durante la Segunda Guerra Mundial, cuando el Servicio de Salud Pública de los Estados Unidos y el Servicio Selectivo se embarcaron en un proyecto a gran escala para eliminar a todos los hombres sifilíticos llamados a filas. La prueba de sífilis de un individuo implica extraerle una muestra de sangre y luego analizarla para determinar la presencia o ausencia de sífilis. En ese momento, realizar esta prueba era costoso, y realizar la prueba a cada soldado individualmente habría sido muy costoso e ineficiente. ^[3]

Suponiendo que hay soldados, este método de prueba conduce a pruebas separadas. Si una gran proporción de personas están infectadas, entonces este método sería razonable. Sin embargo, en el caso más probable de que solo una proporción muy pequeña de los hombres estén infectados, se puede lograr un esquema de pruebas mucho más eficiente. La viabilidad de un esquema de pruebas más eficaz depende de la siguiente propiedad: los soldados pueden agruparse en grupos, y en cada grupo se pueden combinar las muestras de sangre. La muestra combinada puede luego analizarse para verificar si al menos un soldado del grupo tiene sífilis. Esta es la idea central detrás de las pruebas grupales. Si uno o más de los soldados de este grupo tienen sífilis, entonces se desperdicia una prueba (se deben realizar más pruebas para encontrar qué soldado(s) era). Por otro lado, si nadie en el grupo tiene sífilis, entonces se ahorran muchas pruebas, ya que cada soldado en ese grupo puede eliminarse con una sola prueba. ^[3] ${\displaystyle n}$ ${\displaystyle n}$

Los elementos que hacen que un grupo dé positivo en la prueba se denominan generalmente elementos defectuosos (por ejemplo, las bombillas rotas, los hombres sifilíticos, etc.). A menudo, el número total de elementos se indica como y representa el número de elementos defectuosos si se supone que se conoce. ^[3] ${\displaystyle n}$ ${\displaystyle d}$

Clasificación de problemas de pruebas grupales

Existen dos clasificaciones independientes para los problemas de pruebas grupales: cada problema de pruebas grupales es adaptativo o no adaptativo, y probabilístico o combinatorio. ^[3]

En los modelos probabilísticos, se supone que los elementos defectuosos siguen una distribución de probabilidad y el objetivo es minimizar la cantidad esperada de pruebas necesarias para identificar la defectividad de cada elemento. Por otro lado, con las pruebas de grupo combinatorias, el objetivo es minimizar la cantidad de pruebas necesarias en un "escenario de caso peor" (es decir, crear un algoritmo minmax ) y no se supone ningún conocimiento de la distribución de elementos defectuosos. ^[3]

La otra clasificación, la adaptabilidad, se refiere a qué información se puede utilizar para elegir qué elementos agrupar en una prueba. En general, la elección de qué elementos probar puede depender de los resultados de pruebas anteriores, como en el problema de la bombilla anterior. Un algoritmo que procede realizando una prueba y luego utiliza el resultado (y todos los resultados anteriores) para decidir qué prueba siguiente realizar, se llama adaptativo. Por el contrario, en los algoritmos no adaptativos, todas las pruebas se deciden de antemano. Esta idea se puede generalizar a los algoritmos de múltiples etapas, donde las pruebas se dividen en etapas y cada prueba en la siguiente etapa debe decidirse de antemano, con solo el conocimiento de los resultados de las pruebas en etapas anteriores. Aunque los algoritmos adaptativos ofrecen mucha más libertad en el diseño, se sabe que los algoritmos adaptativos de prueba de grupo no mejoran a los no adaptativos en más de un factor constante en el número de pruebas necesarias para identificar el conjunto de elementos defectuosos. ^{[4] [3]} Además de esto, los métodos no adaptativos suelen ser útiles en la práctica porque se puede proceder con pruebas sucesivas sin analizar primero los resultados de todas las pruebas anteriores, lo que permite una distribución efectiva del proceso de prueba.

Variaciones y ampliaciones

Hay muchas maneras de extender el problema de las pruebas grupales. Una de las más importantes se llama prueba grupal ruidosa y trata sobre una gran suposición del problema original: que las pruebas están libres de errores. Un problema de prueba grupal se llama ruidoso cuando hay alguna posibilidad de que el resultado de una prueba grupal sea erróneo (por ejemplo, que salga positivo cuando la prueba no contenía defectuosos). El modelo de ruido de Bernoulli supone que esta probabilidad es una constante, , pero en general puede depender del número real de defectuosos en la prueba y del número de elementos probados. ^[5] Por ejemplo, el efecto de la dilución se puede modelar diciendo que un resultado positivo es más probable cuando hay más defectuosos (o más defectuosos como fracción del número probado), presentes en la prueba. ^[6] Un algoritmo ruidoso siempre tendrá una probabilidad distinta de cero de cometer un error (es decir, etiquetar mal un elemento). ${\displaystyle q}$

Las pruebas grupales se pueden ampliar considerando escenarios en los que hay más de dos resultados posibles de una prueba. Por ejemplo, una prueba puede tener los resultados y , correspondientes a que no haya defectuosos, un solo defectuoso o un número desconocido de defectuosos mayor que uno. De manera más general, es posible considerar que el conjunto de resultados de una prueba es para algún . ^[3] ${\displaystyle 0,1}$ ${\displaystyle 2^{+}}$ ${\displaystyle {0,1,\ldots ,k^{+}}}$ ${\displaystyle k\in \mathbb {N} }$

Otra extensión es considerar restricciones geométricas sobre qué conjuntos pueden ser probados. El problema de la bombilla anterior es un ejemplo de este tipo de restricción: sólo las bombillas que aparecen consecutivamente pueden ser probadas. De manera similar, los elementos pueden estar dispuestos en un círculo o, en general, en una red, donde las pruebas son caminos disponibles en el grafo. Otro tipo de restricción geométrica sería sobre el número máximo de elementos que pueden ser probados en un grupo, ^[a] o los tamaños de los grupos podrían tener que ser iguales, etc. De manera similar, puede ser útil considerar la restricción de que cualquier elemento dado sólo puede aparecer en un cierto número de pruebas. ^[3]

Existen infinitas formas de seguir remezclando la fórmula básica de las pruebas grupales. Las siguientes elaboraciones darán una idea de algunas de las variantes más exóticas. En el modelo "bueno-mediocre-malo", cada elemento es "bueno", "mediocre" o "malo", y el resultado de una prueba es el tipo del elemento "peor" del grupo. En las pruebas grupales de umbral, el resultado de una prueba es positivo si el número de elementos defectuosos en el grupo es mayor que un valor o proporción de umbral. ^[7] Las pruebas grupales con inhibidores son una variante con aplicaciones en biología molecular. Aquí, hay una tercera clase de elementos llamados inhibidores, y el resultado de una prueba es positivo si contiene al menos un elemento defectuoso y ningún inhibidor. ^[8]

Historia y desarrollo

Invención y progreso inicial

El concepto de prueba grupal fue introducido por primera vez por Robert Dorfman en 1943 en un informe breve ^[2] publicado en la sección Notas de Annals of Mathematical Statistics . ^{[3] [b]} El informe de Dorfman, como todos los primeros trabajos sobre pruebas grupales, se centró en el problema probabilístico y apuntó a utilizar la novedosa idea de las pruebas grupales para reducir el número esperado de pruebas necesarias para eliminar a todos los hombres sifilíticos en un grupo dado de soldados. El método era simple: poner a los soldados en grupos de un tamaño determinado y utilizar pruebas individuales (probar elementos en grupos de tamaño uno) en los grupos positivos para encontrar cuáles estaban infectados. Dorfman tabuló los tamaños de grupo óptimos para esta estrategia contra la tasa de prevalencia de defectos en la población. ^[2] Stephen Samuels ^[10] encontró una solución de forma cerrada para el tamaño de grupo óptimo como una función de la tasa de prevalencia.

Después de 1943, las pruebas grupales se mantuvieron prácticamente intactas durante varios años. Luego, en 1957, Sterrett produjo una mejora en el procedimiento de Dorfman. ^[11] Este nuevo proceso comienza nuevamente realizando pruebas individuales en los grupos positivos, pero se detiene tan pronto como se identifica un defectuoso. Luego, los elementos restantes del grupo se prueban juntos, ya que es muy probable que ninguno de ellos sea defectuoso.

El primer estudio exhaustivo de las pruebas grupales lo realizaron Sobel y Groll en su artículo de 1959 sobre el tema. ^[12] Describieron cinco nuevos procedimientos (además de generalizaciones para casos en los que se desconoce la tasa de prevalencia) y, para el procedimiento óptimo, proporcionaron una fórmula explícita para el número esperado de pruebas que se utilizarían. El artículo también estableció por primera vez la conexión entre las pruebas grupales y la teoría de la información , además de analizar varias generalizaciones del problema de las pruebas grupales y proporcionar algunas aplicaciones nuevas de la teoría.

El resultado fundamental de Peter Ungar en 1960 muestra que si la tasa de prevalencia es , entonces la prueba individual es el procedimiento óptimo de prueba grupal con respecto al número esperado de pruebas, y si es , entonces no es óptimo. Sin embargo, es importante señalar que a pesar de 80 años de esfuerzo de investigación, aún se desconoce el procedimiento óptimo para y un tamaño de población general . ^[13] ${\displaystyle p>p_{u}=(3-{\sqrt {5}})/2\approx 0.38}$ ${\displaystyle p<p_{u}}$ ${\displaystyle p<p_{u}}$ ${\displaystyle n>2}$

Prueba de grupo combinatorio

Las pruebas grupales fueron estudiadas por primera vez en el contexto combinatorio por Li en 1962, ^[14] con la introducción del algoritmo de 2 etapas de Li ${\displaystyle s}$ . ^[3] Li propuso una extensión del 'algoritmo de 2 etapas' de Dorfman a un número arbitrario de etapas que no requerían más de pruebas para garantizar la detección de elementos defectuosos o menos entre ellos. La idea era eliminar todos los elementos en pruebas negativas y dividir los elementos restantes en grupos como se hizo con el grupo inicial. Esto debía hacerse 2 veces antes de realizar pruebas individuales. ${\displaystyle t={\frac {e}{\log _{2}(e)}}d\log _{2}(n)}$ ${\displaystyle d}$ ${\displaystyle n}$ ${\displaystyle s-1}$

Las pruebas de grupo combinatorias en general fueron estudiadas más a fondo por Katona en 1973. ^[15] Katona introdujo la representación matricial de las pruebas de grupo no adaptativas y produjo un procedimiento para encontrar el defectuoso en el caso no adaptativo de 1 defectuoso en no más de pruebas, que también demostró ser óptimo. ${\displaystyle t=\lceil \log _{2}(n)\rceil }$

En general, es difícil encontrar algoritmos óptimos para las pruebas de grupos combinatorios adaptativos y, aunque no se ha determinado la complejidad computacional de las pruebas de grupos, se sospecha que es difícil en alguna clase de complejidad. ^[3] Sin embargo, en 1972 se produjo un avance importante con la introducción del algoritmo de división binaria generalizado. ^[16] El algoritmo de división binaria generalizado funciona realizando una búsqueda binaria en grupos que dan positivo y es un algoritmo simple que encuentra un solo defectuoso en no más del número de pruebas del límite inferior de información.

En escenarios donde hay dos o más defectuosos, el algoritmo de división binaria generalizado aún produce resultados casi óptimos, requiriendo como máximo pruebas por encima del límite inferior de información donde es el número de defectuosos. ^[16] En 2013, Allemann realizó mejoras considerables a esto, logrando que el número requerido de pruebas fuera menor que por encima del límite inferior de información cuando y . ^[17] Esto se logró cambiando la búsqueda binaria en el algoritmo de división binaria a un conjunto complejo de subalgoritmos con grupos de prueba superpuestos. Como tal, el problema de las pruebas de grupo combinatorias adaptativas (con un número conocido o límite superior en el número de defectuosos) se ha resuelto esencialmente, con poco margen para mejoras adicionales. ${\displaystyle d-1}$ ${\displaystyle d}$ ${\displaystyle 0.187d+0.5\log _{2}(d)+5.5}$ ${\displaystyle n/d\geq 38}$ ${\displaystyle d\geq 10}$

Existe una pregunta abierta sobre cuándo la prueba individual es minmax . Hu, Hwang y Wang demostraron en 1981 que la prueba individual es minmax cuando , y que no es minmax cuando . ^[18] Actualmente se conjetura que este límite es preciso: es decir, la prueba individual es minmax si y solo si . ^{[19] [c]} En 2000, Riccio y Colbourn lograron algunos avances al demostrar que para valores grandes de , la prueba individual es minmax cuando . ^[20] ${\displaystyle n\leq \lfloor (5d+1)/2\rfloor }$ ${\displaystyle n>3d}$ ${\displaystyle n\leq 3d}$ ${\displaystyle n}$ ${\displaystyle d\geq n/\log _{3/2}(3)\approx 0.369n}$

Pruebas no adaptativas y probabilísticas

Una de las ideas clave en las pruebas grupales no adaptativas es que se pueden lograr ganancias significativas eliminando el requisito de que el procedimiento de prueba grupal tenga éxito (el problema "combinatorio"), y en cambio permitiéndole tener una probabilidad baja pero no nula de etiquetar incorrectamente cada elemento (el problema "probabilístico"). Se sabe que a medida que el número de elementos defectuosos se acerca al número total de elementos, las soluciones combinatorias exactas requieren significativamente más pruebas que las soluciones probabilísticas, incluso las soluciones probabilísticas permiten solo una probabilidad de error asintóticamente pequeña. ^{[4] [d]}

En esta línea, Chan et al. (2011) introdujeron COMP, un algoritmo probabilístico que no requiere más que pruebas para encontrar hasta defectuosos en artículos con una probabilidad de error no mayor a . ^[5] Esto está dentro de un factor constante del límite inferior. ^[4] ${\displaystyle t=ed(1+\delta )\ln(n)}$ ${\displaystyle d}$ ${\displaystyle n}$ ${\displaystyle n^{-\delta }}$ ${\displaystyle t=O(d\log _{2}n)}$

Chan et al. (2011) también proporcionaron una generalización de COMP a un modelo ruidoso simple, y de manera similar produjeron un límite de rendimiento explícito, que nuevamente fue solo una constante (dependiente de la probabilidad de una prueba fallida) por encima del límite inferior correspondiente. ^{[4] [5]} En general, la cantidad de pruebas requeridas en el caso de ruido de Bernoulli es un factor constante mayor que en el caso sin ruido. ^[5]

Aldridge, Baldassini y Johnson (2014) produjeron una extensión del algoritmo COMP que agregó pasos adicionales de posprocesamiento. ^[21] Demostraron que el rendimiento de este nuevo algoritmo, llamado DD, supera estrictamente al de COMP, y que DD es "esencialmente óptimo" en escenarios donde , comparándolo con un algoritmo hipotético que define un óptimo razonable. El rendimiento de este algoritmo hipotético sugiere que hay margen de mejora cuando , además de sugerir cuánta mejora podría ser esta. ^[21] ${\displaystyle d^{2}\geq n}$ ${\displaystyle d^{2}<n}$

Formalización de pruebas de grupos combinatorios

Esta sección define formalmente las nociones y términos relacionados con las pruebas grupales.

• El vector de entrada , , se define como un vector binario de longitud (es decir, ), y el elemento j -ésimo se denomina defectuoso si y solo si . Además, cualquier elemento no defectuoso se denomina elemento "bueno". ${\displaystyle \mathbf {x} =(x_{1},x_{2},\dots ,x_{n})}$ ${\displaystyle n}$ ${\displaystyle \mathbf {x} \in \{0,1\}^{n}}$ ${\displaystyle x_{j}=1}$

${\displaystyle \mathbf {x} }$se pretende describir el conjunto (desconocido) de elementos defectuosos. La propiedad clave de es que es una entrada implícita . Es decir, no hay conocimiento directo de cuáles son las entradas de, más allá del que se puede inferir a través de una serie de "pruebas". Esto nos lleva a la siguiente definición. ${\displaystyle \mathbf {x} }$ ${\displaystyle \mathbf {x} }$

• Sea un vector de entrada. Un conjunto se denomina prueba . Cuando la prueba es sin ruido , el resultado de una prueba es positivo cuando existe tal que , y el resultado es negativo en caso contrario. ${\displaystyle \mathbf {x} }$ ${\displaystyle S\subseteq \{1,2,\dots ,n\}}$ ${\displaystyle j\in S}$ ${\displaystyle x_{j}=1}$

Por lo tanto, el objetivo de las pruebas de grupo es encontrar un método para elegir una serie "corta" de pruebas que permitan determinar con exactitud o con un alto grado de certeza. ${\displaystyle \mathbf {x} }$

• Se dice que un algoritmo de prueba grupal comete un error si etiqueta incorrectamente un elemento (es decir, etiqueta cualquier elemento defectuoso como no defectuoso o viceversa). Esto no es lo mismo que el resultado de una prueba grupal sea incorrecto. Se dice que un algoritmo tiene cero errores si la probabilidad de que cometa un error es cero. ^[e]
• ${\displaystyle t(d,n)}$denota el número mínimo de pruebas necesarias para encontrar siempre elementos defectuosos entre los que tienen una probabilidad cero de error con cualquier algoritmo de prueba de grupo. Para la misma cantidad, pero con la restricción de que el algoritmo no es adaptativo, se utiliza la notación. ${\displaystyle d}$ ${\displaystyle n}$ ${\displaystyle {\bar {t}}(d,n)}$

Límites generales

Dado que siempre es posible recurrir a pruebas individuales estableciendo para cada , debe ser que . Además, dado que cualquier procedimiento de prueba no adaptativo se puede escribir como un algoritmo adaptativo simplemente realizando todas las pruebas sin tener en cuenta su resultado, . Finalmente, cuando , hay al menos un elemento cuya defectividad debe determinarse (mediante al menos una prueba), y entonces . ${\displaystyle S_{j}=\{j\}}$ ${\displaystyle 1\leq j\leq n}$ ${\displaystyle {\bar {t}}(d,n)\leq n}$ ${\displaystyle t(d,n)\leq {\bar {t}}(d,n)}$ ${\displaystyle 0\neq d\neq n}$ ${\displaystyle 1\leq t(d,n)}$

En resumen (suponiendo ), . ^[f] ${\displaystyle 0\neq d\neq n}$ ${\displaystyle 1\leq t(d,n)\leq {\bar {t}}(d,n)\leq n}$

Límite inferior de información

Se puede describir un límite inferior en el número de pruebas necesarias utilizando la noción de espacio muestral , denotado , que es simplemente el conjunto de posibles colocaciones de defectuosos. Para cualquier problema de prueba de grupo con espacio muestral y cualquier algoritmo de prueba de grupo, se puede demostrar que , donde es el número mínimo de pruebas necesarias para identificar todos los defectuosos con una probabilidad de error cero. Esto se llama límite inferior de información . ^[3] Este límite se deriva del hecho de que después de cada prueba, se divide en dos subconjuntos disjuntos, cada uno correspondiente a uno de los dos resultados posibles de la prueba. ${\displaystyle {\mathcal {S}}}$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle t\geq \lceil \log _{2}{|{\mathcal {S}}|}\rceil }$ ${\displaystyle t}$ ${\displaystyle {\mathcal {S}}}$

Sin embargo, el límite inferior de la información en sí suele ser inalcanzable, incluso para problemas pequeños. ^[3] Esto se debe a que la división de no es arbitraria, ya que debe ser realizable mediante alguna prueba. ${\displaystyle {\mathcal {S}}}$

De hecho, el límite inferior de la información se puede generalizar al caso en el que existe una probabilidad distinta de cero de que el algoritmo cometa un error. De esta forma, el teorema nos da un límite superior para la probabilidad de éxito en función del número de pruebas. Para cualquier algoritmo de prueba grupal que realice pruebas, la probabilidad de éxito, , satisface . Esto se puede reforzar a: . ^{[5] [22]} ${\displaystyle t}$ ${\displaystyle \mathbb {P} ({\textrm {success}})}$ ${\displaystyle \mathbb {P} ({\textrm {success}})\leq t/\log _{2}{n \choose d}}$ ${\displaystyle \mathbb {P} ({\textrm {success}})\leq {\frac {2^{t}}{n \choose d}}}$

Representación de algoritmos no adaptativos

Una configuración típica de prueba grupal. Un algoritmo no adaptativo elige primero la matriz y luego se le da el vector y . El problema es entonces encontrar una estimación para x . ${\displaystyle M}$

Los algoritmos para las pruebas grupales no adaptativas constan de dos fases distintas. En la primera, se decide cuántas pruebas se realizarán y qué elementos se incluirán en cada prueba. En la segunda fase, a menudo denominada paso de decodificación, se analizan los resultados de cada prueba grupal para determinar qué elementos tienen probabilidades de ser defectuosos. La primera fase suele codificarse en una matriz de la siguiente manera. ^[5]

• Supongamos que un procedimiento de prueba grupal no adaptativo para ítems consiste en las pruebas para algunos . La matriz de prueba para este esquema es la matriz binaria, , donde si y solo si (y es cero en caso contrario). ${\displaystyle n}$ ${\displaystyle S_{1},S_{2},\dots ,S_{t}}$ ${\displaystyle t\in \mathbb {N} _{\geq 0}}$ ${\displaystyle t\times n}$ ${\displaystyle M}$ ${\displaystyle (M)_{ij}=1}$ ${\displaystyle j\in S_{i}}$

De esta forma, cada columna representa un elemento y cada fila representa una prueba, con un en la entrada indicando que la prueba incluía el elemento y un indicando lo contrario. ${\displaystyle M}$ ${\displaystyle 1}$ ${\displaystyle (i,j){\textrm {-th}}}$ ${\displaystyle i{\textrm {-th}}}$ ${\displaystyle j{\textrm {-th}}}$ ${\displaystyle 0}$

Además del vector (de longitud ) que describe el conjunto defectuoso desconocido, es común introducir el vector de resultados, que describe los resultados de cada prueba. ${\displaystyle \mathbf {x} }$ ${\displaystyle n}$

• Sea el número de pruebas realizadas por un algoritmo no adaptativo. El vector de resultados , , es un vector binario de longitud (es decir, ) tal que si y solo si el resultado de la prueba fue positivo (es decir, contenía al menos un defecto). ^[g] ${\displaystyle t}$ ${\displaystyle \mathbf {y} =(y_{1},y_{2},\dots ,y_{t})}$ ${\displaystyle t}$ ${\displaystyle \mathbf {y} \in \{0,1\}^{t}}$ ${\displaystyle y_{i}=1}$ ${\displaystyle i{\textrm {-th}}}$

Con estas definiciones, el problema no adaptativo puede replantearse de la siguiente manera: primero se elige una matriz de prueba, , después de lo cual se devuelve el vector . Luego el problema consiste en analizar para encontrar alguna estimación para . ${\displaystyle M}$ ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {x} }$

En el caso ruidoso más simple, donde hay una probabilidad constante, , de que una prueba de grupo tenga un resultado erróneo, se considera un vector binario aleatorio, , donde cada entrada tiene una probabilidad de ser , y es en caso contrario. El vector que se devuelve es entonces , con la adición habitual (equivalentemente, esta es la operación XOR elemento por elemento ). Un algoritmo ruidoso debe estimar utilizando (es decir, sin conocimiento directo de ). ^[5] ${\displaystyle q}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle q}$ ${\displaystyle 1}$ ${\displaystyle 0}$ ${\displaystyle {\hat {\mathbf {y} }}=\mathbf {y} +\mathbf {v} }$ ${\displaystyle (\mathbb {Z} /2\mathbb {Z} )^{n}}$ ${\displaystyle \mathbf {x} }$ ${\displaystyle {\hat {\mathbf {y} }}}$ ${\displaystyle \mathbf {y} }$

Límites para algoritmos no adaptativos

La representación matricial permite demostrar algunos límites en las pruebas de grupos no adaptativos. El enfoque refleja el de muchos diseños deterministas, donde se consideran matrices separables, como se define a continuación. ^[3] ${\displaystyle d}$

• Una matriz binaria, , se denomina -separable si cada suma booleana (OR lógico) de cualquiera de sus columnas es distinta. Además, la notación -separable indica que cada suma de cualquiera de hasta las columnas de es distinta. (Esto no es lo mismo que ser -separable para cada ). ${\displaystyle M}$ ${\displaystyle d}$ ${\displaystyle d}$ ${\displaystyle {\bar {d}}}$ ${\displaystyle d}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle k}$ ${\displaystyle k\leq d}$

Cuando se trata de una matriz de prueba, la propiedad de ser -separable ( -separable) es equivalente a poder distinguir entre (hasta) defectos. Sin embargo, no garantiza que esto sea sencillo. Una propiedad más fuerte, llamada disyunción , sí lo hace. ${\displaystyle M}$ ${\displaystyle d}$ ${\displaystyle {\bar {d}}}$ ${\displaystyle d}$

• Una matriz binaria se denomina disyuntiva si la suma booleana de sus columnas no contiene ninguna otra columna. (En este contexto, se dice que una columna A contiene una columna B si por cada índice donde B tiene un 1, A también tiene un 1.) ${\displaystyle M}$ ${\displaystyle d}$ ${\displaystyle d}$

Una propiedad útil de las matrices de prueba disyuntivas es que, con hasta defectuosos, cada elemento no defectuoso aparecerá en al menos una prueba cuyo resultado sea negativo. Esto significa que existe un procedimiento simple para encontrar los defectuosos: simplemente elimine todos los elementos que aparezcan en una prueba negativa. ${\displaystyle d}$ ${\displaystyle d}$

Utilizando las propiedades de las matrices -separables y -disyuntivas se puede demostrar lo siguiente para el problema de identificar defectuosos entre el total de artículos. ^[4] ${\displaystyle d}$ ${\displaystyle d}$ ${\displaystyle d}$ ${\displaystyle n}$

1. El número de pruebas necesarias para una probabilidad de error promedio asintóticamente pequeña varía como . ${\displaystyle O(d\log _{2}n)}$
2. El número de pruebas necesarias para una probabilidad máxima de error asintóticamente pequeña varía como . ${\displaystyle O(d^{2}\log _{2}n)}$
3. El número de pruebas necesarias para una probabilidad de error cero varía como . ${\displaystyle O\left({\frac {d^{2}\log _{2}n}{\log _{2}d}}\right)}$

Algoritmo generalizado de división binaria

Una ilustración del algoritmo de división binaria generalizado donde hay 8 defectuosos y 135 artículos en total. Aquí, , y la primera prueba da un resultado negativo, por lo que cada artículo se declara no defectuoso. Por lo tanto, quedan 119 artículos, por lo que . Este segundo grupo da un resultado positivo, por lo que se utiliza una búsqueda binaria para encontrar un defectuoso. Una vez hecho esto, se repite todo el proceso, calculando un nuevo usando solo aquellos artículos cuya defectividad no se ha determinado. ${\displaystyle 2^{\alpha _{1}}=16}$ ${\displaystyle 2^{\alpha _{2}}=8}$ ${\displaystyle \alpha }$

El algoritmo de división binaria generalizado es un algoritmo de prueba grupal adaptativo esencialmente óptimo que encuentra o menos defectuosos entre los elementos de la siguiente manera: ^{[3] [16]} ${\displaystyle d}$ ${\displaystyle n}$

1. Si es así , pruebe los elementos individualmente. De lo contrario, configure y . ${\displaystyle n\leq 2d-2}$ ${\displaystyle n}$ ${\displaystyle l=n-d+1}$ ${\displaystyle \alpha =\lfloor \log _{2}{l/d}\rfloor }$
2. Pruebe un grupo de tamaño . Si el resultado es negativo, cada elemento del grupo se declara no defectuoso; establezca y vaya al paso 1. De lo contrario, utilice una búsqueda binaria para identificar un elemento defectuoso y un número no especificado, llamado , de elementos no defectuosos; establezca y . Vaya al paso 1. ${\displaystyle 2^{\alpha }}$ ${\displaystyle n:=n-2^{\alpha }}$ ${\displaystyle x}$ ${\displaystyle n:=n-1-x}$ ${\displaystyle d:=d-1}$

El algoritmo de división binaria generalizado no requiere más que pruebas donde . ^[3] ${\displaystyle T}$ ${\displaystyle T={\begin{cases}n&n\leq 2d-2\\(\alpha +2)d+p-1&n\geq 2d-1\end{cases}}}$

Para valores grandes, se puede demostrar que , ^[3] lo que se compara favorablemente con las pruebas requeridas para el algoritmo de la etapa de Li. De hecho, el algoritmo de división binaria generalizado está cerca de ser óptimo en el siguiente sentido. Cuando se puede demostrar que , donde es el límite inferior de la información. ^{[3] [16]} ${\displaystyle n/d}$ ${\displaystyle T\rightarrow d\log _{2}(n/d)}$ ${\displaystyle t={\frac {e}{\log _{2}e}}d\log _{2}\left({\frac {n}{d}}\right)}$ ${\displaystyle s}$ ${\displaystyle d\geq 2}$ ${\displaystyle T-B_{I}(d,n)\leq (d-1)}$ ${\displaystyle B_{I}(d,n)=\left\lceil \log _{2}\sum _{i=0}^{d}{n \choose i}\right\rceil }$

Algoritmos no adaptativos

Los algoritmos de prueba de grupo no adaptativos tienden a suponer que se conoce el número de defectuosos, o al menos un buen límite superior para ellos. ^[5] Esta cantidad se denota en esta sección. Si no se conocen límites, existen algoritmos no adaptativos con baja complejidad de consulta que pueden ayudar a estimar . ^[23] ${\displaystyle d}$ ${\displaystyle d}$

Búsqueda de correspondencia ortogonal combinatoria (COMP)

Ilustración del algoritmo COMP. COMP identifica el elemento a como defectuoso y el elemento b como no defectuoso. Sin embargo, etiqueta incorrectamente a c como defectuoso, ya que está “oculto” por elementos defectuosos en cada prueba en la que aparece.

Combinatorial Orthogonal Matching Pursuit, o COMP, es un algoritmo simple de prueba grupal no adaptativo que constituye la base de los algoritmos más complicados que siguen en esta sección.

En primer lugar, cada entrada de la matriz de prueba se elige con iid o con probabilidad . ${\displaystyle 1}$ ${\displaystyle 1/d}$ ${\displaystyle 0}$

El paso de decodificación se realiza por columnas (es decir, por elemento). Si todas las pruebas en las que aparece un elemento son positivas, entonces el elemento se declara defectuoso; de lo contrario, se supone que el elemento no es defectuoso. O, de manera equivalente, si un elemento aparece en cualquier prueba cuyo resultado es negativo, el elemento se declara no defectuoso; de lo contrario, se supone que el elemento es defectuoso. Una propiedad importante de este algoritmo es que nunca crea falsos negativos , aunque se produce un falso positivo cuando todas las ubicaciones con unos en la j -ésima columna de (que corresponde a un elemento no defectuoso j ) están "ocultas" por los unos de otras columnas correspondientes a elementos defectuosos. ${\displaystyle M}$

El algoritmo COMP no requiere más que pruebas para tener una probabilidad de error menor o igual a . ^[5] Esto está dentro de un factor constante del límite inferior para la probabilidad promedio de error anterior. ${\displaystyle ed(1+\delta )\ln(n)}$ ${\displaystyle n^{-\delta }}$

En el caso ruidoso, se relaja el requisito del algoritmo COMP original de que el conjunto de ubicaciones de unos en cualquier columna correspondiente a un elemento positivo esté completamente contenido en el conjunto de ubicaciones de unos en el vector de resultados. En cambio, se permite una cierta cantidad de “desajustes”; esta cantidad de desajustes depende tanto de la cantidad de unos en cada columna como del parámetro de ruido, . Este algoritmo COMP ruidoso no requiere más que pruebas para lograr una probabilidad de error de como máximo . ^[5] ${\displaystyle M}$ ${\displaystyle q}$ ${\displaystyle 4.36({\sqrt {\delta }}+{\sqrt {1+\delta }})^{2}(1-2q)^{-2}d\log _{2}{n}}$ ${\displaystyle n^{-\delta }}$

Defectuosos definidos (DD)

El método de defectos definidos (DD) es una extensión del algoritmo COMP que intenta eliminar los falsos positivos. Se ha demostrado que las garantías de rendimiento del DD superan estrictamente las del algoritmo COMP. ^[21]

El paso de decodificación utiliza una propiedad útil del algoritmo COMP: cada elemento que COMP declara como no defectuoso ciertamente no lo es (es decir, no hay falsos negativos). Procede de la siguiente manera.

1. Primero se ejecuta el algoritmo COMP y se eliminan todos los elementos que no son defectuosos. Todos los elementos restantes son ahora "posiblemente defectuosos".
2. A continuación, el algoritmo analiza todas las pruebas positivas. Si un elemento aparece como el único "posible defectuoso" en una prueba, entonces debe ser defectuoso, por lo que el algoritmo lo declara defectuoso.
3. Se supone que todos los demás artículos no tienen defectos. La justificación de este último paso se basa en el supuesto de que el número de artículos defectuosos es mucho menor que el número total de artículos.

Tenga en cuenta que los pasos 1 y 2 nunca cometen errores, por lo que el algoritmo solo puede cometer errores si declara que un artículo defectuoso no lo es. Por lo tanto, el algoritmo DD solo puede crear falsos negativos.

COMP secuencial (SCOMP)

SCOMP (Sequential COMP) es un algoritmo que aprovecha el hecho de que DD no comete errores hasta el último paso, donde se supone que los elementos restantes no son defectuosos. Sea . Una prueba positiva se dice que está explicada por si contiene al menos un elemento en . La observación clave con SCOMP es que el conjunto de elementos defectuosos encontrados por DD puede no explicar cada prueba positiva, y que cada prueba no explicada debe contener un elemento defectuoso oculto. ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle K}$

El algoritmo procede de la siguiente manera.

1. Realice los pasos 1 y 2 del algoritmo DD para obtener , una estimación inicial para el conjunto de defectuosos. ${\displaystyle K}$
2. Si explica cada prueba positiva, termina el algoritmo: es la estimación final para el conjunto de defectuosos. ${\displaystyle K}$ ${\displaystyle K}$
3. Si hay alguna prueba sin explicación, busque la "posible defectuosa" que aparezca en la mayor cantidad de pruebas sin explicación y declárela como defectuosa (es decir, agréguela al conjunto ). Vaya al paso 2. ${\displaystyle K}$

En simulaciones, se ha demostrado que SCOMP funciona casi de manera óptima. ^[21]

Pooles polinómicos (PP)

Un algoritmo determinista que garantiza la identificación exacta de hasta positivos es Polynomial Pools (PP). . ^[24] El algoritmo es para la construcción de la matriz de agrupamiento , que se puede utilizar directamente para decodificar las observaciones en . De manera similar a COMP, una muestra se decodifica de acuerdo con la relación: , donde representa la multiplicación elemento por elemento y es la columna n de . Dado que el paso de decodificación no es difícil, PP está especializado para generar . ${\displaystyle d}$ ${\displaystyle M}$ ${\displaystyle y}$ ${\displaystyle x_{i}=1~~{\text{ if }}~~M(:,i)~.*~y=M(:,i)}$ ${\displaystyle .*}$ ${\displaystyle M(:,i)}$ ${\displaystyle i}$ ${\displaystyle M}$ ${\displaystyle M}$

Formación de grupos

Diseño de un grupo con muestras (azul) de un conjunto de muestras totales utilizando el algoritmo Polynomial Pools ${\displaystyle q^{c-1}=9}$ ${\displaystyle n=q^{c}=27}$

Un grupo/pool se genera utilizando una relación polinómica que especifica los índices de las muestras contenidas en cada pool. Un conjunto de parámetros de entrada determina el algoritmo. Para un número primo y un entero, cualquier potencia prima se define por . Para un parámetro de dimensión, el número total de muestras es y el número de muestras por pool es . Además, el campo finito de orden se denota por (es decir, los enteros definidos por operaciones aritméticas especiales que aseguran que la adición y la multiplicación en permanezcan en ). El método organiza cada muestra en una cuadrícula y la representa por coordenadas . Las coordenadas se calculan de acuerdo con una relación polinómica utilizando los enteros , ${\displaystyle \ell }$ ${\displaystyle p>1}$ ${\displaystyle n\geq 1}$ ${\displaystyle q=p^{n}}$ ${\displaystyle c\geq 2}$ ${\displaystyle n=q^{c}}$ ${\displaystyle q^{c-1}}$ ${\displaystyle q}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle \{0,1,2,\ldots ,q-1\}}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle x=(u,v)}$ ${\displaystyle 1\leq l\leq c-1}$ ${\displaystyle 0\leq u_{i_{l}}\leq q-1}$

${\displaystyle v~=~a^{c-1}~u_{i_{c-1}}+\cdots +a~u_{i_{1}}+b,\quad a,b,u_{i_{l}}\in \mathbb {F} _{q}.}$

La combinación de recorrer los valores se representa mediante un conjunto con elementos de una secuencia de números enteros, es decir, , donde . Sin pérdida de generalidad, la combinación es tal que se repite cada vez, se repite cada vez hasta que se repite solo una vez. Las fórmulas que calculan los índices de muestra y, por lo tanto, los grupos correspondientes, para fijos y , se dan mediante ${\displaystyle u_{i_{l}}}$ ${\displaystyle q^{c-1}}$ ${\displaystyle d-1}$ ${\displaystyle u_{i_{1}}\times \cdots \times u_{i_{c-1}}=\{(i_{1},\ldots ,i_{c-1})\}}$ ${\displaystyle 0\leq i_{l}\leq q-1}$ ${\displaystyle i_{d-1}}$ ${\displaystyle q}$ ${\displaystyle i_{d-2}}$ ${\displaystyle q^{2}}$ ${\displaystyle i_{1}}$ ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle {\begin{aligned}u_{i}&=\sum _{l=1}^{c-1}~q^{d-1-l}~i_{l}\\v_{u_{i}}&=\sum _{l=1}^{c-1}~a^{l}~i_{l}+b\quad ({\text{computed in }}\mathbb {F} _{q})\\x_{qu_{i}+v_{u_{i}}}&=(u_{i},v_{u_{i}})\end{aligned}}}$

Los cálculos en se pueden implementar con bibliotecas de software disponibles públicamente para campos finitos, cuando es una potencia prima. Cuando es un número primo, entonces los cálculos en se simplifican a aritmética de módulo, es decir, . En la siguiente tabla se muestra un ejemplo de cómo generar un grupo cuando , mientras que en la figura anterior se muestra la selección correspondiente de muestras. ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle q}$ ${\displaystyle q}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle v_{u_{i}}=(\sum _{l=1}^{c-1}a^{l}i_{l}+b)~{\text{mod}}~q}$ ${\displaystyle \ell }$ ${\displaystyle a=1,b=0,c=2}$

Este método utiliza pruebas para identificar con exactitud hasta los positivos entre las muestras. Por este motivo, el PP es particularmente eficaz para muestras de gran tamaño, ya que el número de pruebas crece solo linealmente con respecto a mientras que las muestras crecen exponencialmente con este parámetro. Sin embargo, el PP también puede ser eficaz para muestras de tamaño pequeño. ^[24] ${\displaystyle q(c-1)(d+1)}$ ${\displaystyle d}$ ${\displaystyle n=q^{c}}$ ${\displaystyle c}$

Ejemplos de aplicaciones

La generalidad de la teoría de pruebas grupales la presta a muchas aplicaciones diversas, incluyendo la detección de clones, la localización de cortocircuitos eléctricos; ^[3] redes informáticas de alta velocidad; ^[25] exámenes médicos, búsqueda de cantidades, estadísticas; ^[18] aprendizaje automático, secuenciación de ADN; ^[26] criptografía; ^{[27] [28]} y análisis forense de datos. ^[29] Esta sección proporciona una breve descripción general de una pequeña selección de estas aplicaciones.

Canales de acceso múltiple

Ilustración de un canal de acceso múltiple que muestra un mensaje exitoso y una colisión de mensajes

Un canal multiacceso es un canal de comunicación que conecta a muchos usuarios a la vez. Todos los usuarios pueden escuchar y transmitir en el canal, pero si más de un usuario transmite al mismo tiempo, las señales colisionan y se reducen a ruido ininteligible. Los canales multiacceso son importantes para diversas aplicaciones del mundo real, en particular las redes de computadoras inalámbricas y las redes telefónicas. ^[30]

Un problema importante con los canales multiacceso es cómo asignar tiempos de transmisión a los usuarios para que sus mensajes no colisionen. Un método simple es dar a cada usuario su propio intervalo de tiempo en el que transmitir, lo que requiere intervalos. (Esto se llama multiplexación por división de tiempo o TDM). Sin embargo, esto es muy ineficiente, ya que asignará intervalos de transmisión a usuarios que pueden no tener un mensaje, y generalmente se supone que solo unos pocos usuarios querrán transmitir en un momento dado; de lo contrario, un canal multiacceso no es práctico en primer lugar. ${\displaystyle n}$

En el contexto de las pruebas de grupo, este problema se suele abordar dividiendo el tiempo en "épocas" de la siguiente manera. ^[3] Un usuario se denomina "activo" si tiene un mensaje al comienzo de una época. (Si se genera un mensaje durante una época, el usuario solo se activa al comienzo de la siguiente). Una época termina cuando todos los usuarios activos han transmitido con éxito su mensaje. El problema es entonces encontrar todos los usuarios activos en una época dada y programar un tiempo para que transmitan (si aún no lo han hecho con éxito). Aquí, una prueba en un conjunto de usuarios corresponde a aquellos usuarios que intentan una transmisión. Los resultados de la prueba son el número de usuarios que intentaron transmitir y , que corresponden respectivamente a ningún usuario activo, exactamente un usuario activo (mensaje exitoso) o más de un usuario activo (colisión de mensajes). Por lo tanto, utilizando un algoritmo de prueba de grupo adaptativo con resultados , se puede determinar qué usuarios desean transmitir en la época. De esta manera, a cualquier usuario que aún no haya realizado una transmisión exitosa se le puede asignar un espacio para transmitir, sin desperdiciar tiempo a usuarios inactivos. ${\displaystyle 0,1,}$ ${\displaystyle 2^{+}}$ ${\displaystyle \{0,1,2^{+}\}}$

Aprendizaje automático y detección comprimida

El aprendizaje automático es un campo de la informática que tiene muchas aplicaciones de software, como la clasificación de ADN, la detección de fraudes y la publicidad dirigida. Uno de los principales subcampos del aprendizaje automático es el problema del "aprendizaje por ejemplos", en el que la tarea consiste en aproximar una función desconocida cuando se le da su valor en una serie de puntos específicos. ^[3] Como se describe en esta sección, este problema de aprendizaje de funciones se puede abordar con un enfoque de prueba grupal.

En una versión simple del problema, hay una función desconocida, donde , y (usando aritmética lógica: la suma es OR lógico y la multiplicación es AND lógico). Aquí es ' sparse', lo que significa que como máximo sus entradas son . El objetivo es construir una aproximación a usando evaluaciones puntuales, donde es lo más pequeño posible. ^[4] (La recuperación exacta corresponde a algoritmos de error cero, mientras que se aproxima mediante algoritmos que tienen una probabilidad de error distinta de cero). ${\displaystyle f:\{0,1\}^{N}\to \{0,1\}}$ ${\displaystyle f({\textbf {x}})={\textbf {a}}\cdot {\textbf {x}}}$ ${\displaystyle {\textbf {a}}\in \{0,1\}^{N}}$ ${\displaystyle {\textbf {a}}}$ ${\displaystyle d}$ ${\displaystyle d\ll N}$ ${\displaystyle 1}$ ${\displaystyle f}$ ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle f}$ ${\displaystyle f}$

En este problema, recuperar es equivalente a encontrar . Además, si y solo si hay algún índice, , donde . Por lo tanto, este problema es análogo a un problema de prueba de grupo con defectuosos y artículos totales. Las entradas de son los artículos, que son defectuosos si son , especifica una prueba, y una prueba es positiva si y solo si . ^[4] ${\displaystyle f}$ ${\displaystyle {\textbf {a}}}$ ${\displaystyle f({\textbf {p}})=1}$ ${\displaystyle n}$ ${\displaystyle {\textbf {a}}_{n}={\textbf {p}}_{n}=1}$ ${\displaystyle d}$ ${\displaystyle n}$ ${\displaystyle {\textbf {a}}}$ ${\displaystyle 1}$ ${\displaystyle {\textbf {p}}}$ ${\displaystyle f({\textbf {p}})=1}$

En realidad, a menudo nos interesarán funciones más complicadas, como , donde . La detección comprimida , que está estrechamente relacionada con las pruebas de grupo, se puede utilizar para resolver este problema. ^[4] ${\displaystyle f:\mathbb {C} ^{N}\to \mathbb {C} }$ ${\displaystyle f({\textbf {x}})={\textbf {a}}\cdot {\textbf {x}}}$

En la detección comprimida, el objetivo es reconstruir una señal, , tomando una serie de mediciones. Estas mediciones se modelan tomando el producto escalar de con un vector elegido. ^[h] El objetivo es utilizar una pequeña cantidad de mediciones, aunque esto normalmente no es posible a menos que se suponga algo sobre la señal. Una de esas suposiciones (que es común ^{[33] [34]} ) es que solo una pequeña cantidad de entradas de son significativas , lo que significa que tienen una gran magnitud. Dado que las mediciones son productos escalares de , la ecuación se cumple, donde es una matriz que describe el conjunto de mediciones que se han elegido y es el conjunto de resultados de las mediciones. Esta construcción muestra que la detección comprimida es una especie de prueba de grupo "continua". ${\displaystyle {\textbf {v}}\in \mathbb {C} ^{N}}$ ${\displaystyle {\textbf {v}}}$ ${\displaystyle {\textbf {v}}}$ ${\displaystyle {\textbf {v}}}$ ${\displaystyle M{\textbf {v}}={\textbf {q}}}$ ${\displaystyle M}$ ${\displaystyle t\times N}$ ${\displaystyle \mathbf {q} }$

La principal dificultad en la detección comprimida es identificar qué entradas son significativas. ^[33] Una vez hecho esto, hay una variedad de métodos para estimar los valores reales de las entradas. ^[35] Esta tarea de identificación se puede abordar con una aplicación simple de prueba de grupo. Aquí una prueba de grupo produce un número complejo: la suma de las entradas que se prueban. El resultado de una prueba se llama positivo si produce un número complejo con una magnitud grande, lo que, dada la suposición de que las entradas significativas son escasas, indica que al menos una entrada significativa está contenida en la prueba.

Existen construcciones deterministas explícitas para este tipo de algoritmo de búsqueda combinatoria, que requieren mediciones. ^[36] Sin embargo, al igual que con las pruebas de grupo, estas son subóptimas, y las construcciones aleatorias (como COMP) a menudo pueden recuperarse de manera sublineal en . ^[35] ${\displaystyle d2^{(\log _{2}\log _{2}N)^{O(1)}}}$ ${\displaystyle f}$ ${\displaystyle N}$

Diseño de ensayo multiplex para pruebas de COVID-19

Durante una pandemia como el brote de COVID-19 en 2020, los ensayos de detección de virus a veces se realizan utilizando diseños de pruebas grupales no adaptativas. ^{[37] [38] [39]} Un ejemplo fue proporcionado por el proyecto Origami Assays que lanzó diseños de pruebas grupales de código abierto para ejecutarse en una placa de 96 pocillos estándar de laboratorio. ^[40]

Plantilla de papel de ensayo de origami para el diseño de pruebas grupales

En un entorno de laboratorio, uno de los desafíos de las pruebas grupales es que la construcción de las mezclas puede llevar mucho tiempo y ser difícil de hacer con precisión a mano. Los ensayos de origami proporcionaron una solución alternativa a este problema de construcción al proporcionar plantillas de papel para guiar al técnico sobre cómo distribuir las muestras de pacientes en los pocillos de prueba. ^[41]

Con los diseños de prueba de grupo más grande (XL3), fue posible analizar 1120 muestras de pacientes en 94 pocillos de ensayo. Si la tasa de verdaderos positivos era lo suficientemente baja, no era necesario realizar pruebas adicionales.

Análisis forense de datos

La ciencia forense de datos es un campo dedicado a encontrar métodos para recopilar evidencia digital de un delito. Estos delitos suelen implicar que un adversario modifique los datos, documentos o bases de datos de una víctima, por ejemplo, alterando registros fiscales, ocultando un virus o modificando datos personales por un ladrón de identidad. ^[29]

Una herramienta común en la investigación forense de datos es el hash criptográfico unidireccional . Se trata de una función que toma los datos y, a través de un procedimiento difícil de revertir, produce un número único llamado hash. ^[i] Los hashes, que suelen ser mucho más cortos que los datos, nos permiten comprobar si los datos han cambiado sin tener que almacenar copias completas de la información de forma desperdiciada: el hash de los datos actuales se puede comparar con un hash anterior para determinar si se han producido cambios. Una propiedad desafortunada de este método es que, aunque es fácil saber si los datos han sido modificados, no hay forma de determinar cómo: es decir, es imposible recuperar qué parte de los datos ha cambiado. ^[29]

Una forma de evitar esta limitación es almacenar más hashes (ahora de subconjuntos de la estructura de datos) para delimitar dónde se ha producido el ataque. Sin embargo, para encontrar la ubicación exacta del ataque con un enfoque ingenuo, sería necesario almacenar un hash para cada dato de la estructura, lo que anularía el objetivo de los hashes en primer lugar (también se podría almacenar una copia normal de los datos). Las pruebas de grupo se pueden utilizar para reducir drásticamente la cantidad de hashes que se deben almacenar. Una prueba se convierte en una comparación entre los hashes almacenados y los actuales, lo que es positivo cuando hay una discordancia. Esto indica que al menos un dato editado (que se considera defectuoso en este modelo) está contenido en el grupo que generó el hash actual. ^[29]

De hecho, la cantidad de hashes necesarios es tan baja que, junto con la matriz de prueba a la que hacen referencia, pueden incluso almacenarse dentro de la estructura organizativa de los propios datos. Esto significa que, en lo que respecta a la memoria, la prueba se puede realizar "gratis". (Esto es así con la excepción de una clave maestra/contraseña que se utiliza para determinar en secreto la función de hash.) ^[29]

Notas

1. El problema original que Dorfman estudió era de esta naturaleza (aunque no lo tuvo en cuenta), ya que en la práctica, sólo se podía reunir una cierta cantidad de sueros sanguíneos antes de que el procedimiento de prueba se volviera poco fiable. Esta fue la razón principal por la que el procedimiento de Dorfman no se aplicó en ese momento. ^[3]
2. Sin embargo, como suele suceder en matemáticas, las pruebas grupales se han reinventado varias veces desde entonces, a menudo en el contexto de aplicaciones. Por ejemplo, Hayes ideó de forma independiente la idea de consultar grupos de usuarios en el contexto de protocolos de comunicación de acceso múltiple en 1978. ^[9]
3. A esto a veces se le llama la conjetura de Hu-Hwang-Wang.
4. El número de pruebas, , debe escalar como para los diseños deterministas, en comparación con los diseños que permiten probabilidades de error arbitrariamente pequeñas (como y ). ^[4] ${\displaystyle t}$ ${\displaystyle t=O\left(d^{2}\log _{d}n\right)}$ ${\displaystyle t=O(d\log _{2}n)}$ ${\displaystyle d\to \infty }$ ${\displaystyle n\to \infty }$
5. Hay que tener cuidado de distinguir entre cuando una prueba arroja un resultado falso y cuando el procedimiento de prueba grupal falla en su totalidad. Es posible cometer un error sin ninguna prueba incorrecta y no cometerlo con algunas pruebas incorrectas. La mayoría de los algoritmos combinatorios modernos tienen una probabilidad de error distinta de cero (incluso sin pruebas erróneas), ya que esto reduce significativamente la cantidad de pruebas necesarias.
6. De hecho, es posible hacerlo mucho mejor. Por ejemplo, el algoritmo de Li en etapas proporciona una construcción explícita donde . ${\displaystyle s}$ ${\displaystyle t\leq {\frac {e}{\log _{2}e}}d\log _{2}{(n/d)}}$
7. Alternativamente, se puede definir mediante la ecuación , donde la multiplicación es AND lógico ( ) y la adición es OR lógico ( ). Aquí, tendrá una en posición si y solo si y son ambos para cualquier . Es decir, si y solo si se incluyó al menos un elemento defectuoso en la prueba. ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {y} :=M\mathbf {x} }$ ${\displaystyle \wedge }$ ${\displaystyle \vee }$ ${\displaystyle \mathbf {y} }$ ${\displaystyle 1}$ ${\displaystyle i}$ ${\displaystyle (M)_{i,j}}$ ${\displaystyle \mathbf {x} _{j}}$ ${\displaystyle 1}$ ${\displaystyle j}$ ${\displaystyle i{\textrm {-th}}}$
8. Este tipo de medición se utiliza en muchas aplicaciones. Por ejemplo, en ciertos tipos de cámaras digitales ^[31] o máquinas de resonancia magnética ^[32] , donde las limitaciones de tiempo requieren que se tomen solo una pequeña cantidad de mediciones.
9. Más formalmente, los hashes tienen una propiedad llamada resistencia a la colisión, que consiste en que la probabilidad de que el mismo hash resulte de diferentes entradas es muy baja para datos de un tamaño adecuado. En la práctica, la probabilidad de que dos entradas diferentes puedan producir el mismo hash suele ignorarse.

Referencias

Citas

1. Colbourn, Charles J.; Dinitz, Jeffrey H. (2007), Manual de diseños combinatorios (2.ª ed.), Boca Raton: Chapman & Hall/ CRC, pág. 574, Sección 46: Diseños de agrupación, ISBN 978-1-58488-506-1
2. Dorfman, Robert (diciembre de 1943), "La detección de miembros defectuosos de grandes poblaciones", The Annals of Mathematical Statistics , 14 (4): 436–440, doi : 10.1214/aoms/1177731363 , JSTOR  2235930
3. Ding-Zhu, Du; Hwang, Frank K. (1993). Pruebas de grupos combinatorios y sus aplicaciones . Singapur: World Scientific. ISBN 978-9810212933.
4. Atia, George Kamal; Saligrama, Venkatesh (marzo de 2012). "Detección comprimida booleana y pruebas de grupos ruidosos". IEEE Transactions on Information Theory . 58 (3): 1880–1901. arXiv : 0907.1061 . doi :10.1109/TIT.2011.2178156. S2CID  8946216.
5. Chun Lam Chan; Pak Hou Che; Jaggi, Sidharth; Saligrama, Venkatesh (1 de septiembre de 2011). "Pruebas de grupo probabilísticas no adaptativas con mediciones ruidosas: límites casi óptimos con algoritmos eficientes". 49.ª Conferencia Anual Allerton sobre Comunicación, Control y Computación . págs. 1832–9. arXiv : 1107.4540 . doi :10.1109/Allerton.2011.6120391. ISBN . 978-1-4577-1817-5.S2CID8408114  .​
6. Hung, M.; Swallow, William H. (marzo de 1999). "Robustez de las pruebas grupales en la estimación de proporciones". Biometrics . 55 (1): 231–7. doi :10.1111/j.0006-341X.1999.00231.x. PMID  11318160. S2CID  23389365.
7. Chen, Hong-Bin; Fu, Hung-Lin (abril de 2009). "Algoritmos no adaptativos para pruebas de grupos umbral". Matemáticas Aplicadas Discretas . 157 (7): 1581–1585. doi : 10.1016/j.dam.2008.06.003 .
8. De Bonis, Annalisa (20 de julio de 2007). "Nuevas estructuras combinatorias con aplicaciones para pruebas de grupo eficientes con inhibidores". Journal of Combinatorial Optimization . 15 (1): 77–94. doi :10.1007/s10878-007-9085-1. S2CID  207188798.
9. Hayes, J. (agosto de 1978). "Una técnica adaptativa para la distribución local". IEEE Transactions on Communications . 26 (8): 1178–86. doi :10.1109/TCOM.1978.1094204.
10. Samuels, Stephen (1978). "La solución exacta al problema de las pruebas grupales en dos etapas". Technometrics . 20 (4): 497–500. doi : 10.1080/00401706.1978.10489706 .
11. Sterrett, Andrew (diciembre de 1957). "Sobre la detección de miembros defectuosos de grandes poblaciones". Anales de estadística matemática . 28 (4): 1033–6. doi : 10.1214/aoms/1177706807 .
12. Sobel, Milton; Groll, Phyllis A. (septiembre de 1959). "Pruebas grupales para eliminar eficientemente todos los defectuosos en una muestra binomial". Bell System Technical Journal . 38 (5): 1179–1252. doi :10.1002/j.1538-7305.1959.tb03914.x.
13. Ungar, Peter (febrero de 1960). "Puntos de corte en pruebas de grupo". Communications on Pure and Applied Mathematics . 13 (1): 49–54. doi : 10.1002/cpa.3160130105 .
14. Li, Chou Hsiung (junio de 1962). "Un método secuencial para el cribado de variables experimentales". Journal of the American Statistical Association . 57 (298): 455–477. doi :10.1080/01621459.1962.10480672.
15. Katona, Gyula OH (1973). "Un estudio de la teoría combinatoria". Problemas de búsqueda combinatoria . Holanda Septentrional. págs. 285-308. ISBN 978-0-7204-2262-7.
16. Hwang, Frank K. (septiembre de 1972). "Un método para detectar todos los miembros defectuosos en una población mediante pruebas de grupo". Revista de la Asociación Estadounidense de Estadística . 67 (339): 605–608. doi :10.2307/2284447. JSTOR  2284447.
17. Allemann, Andreas (2013). "Un algoritmo eficiente para pruebas de grupos combinatorios". Teoría de la información, combinatoria y teoría de búsqueda . Apuntes de clase en informática. Vol. 7777. págs. 569–596. doi :10.1007/978-3-642-36899-8_29. ISBN 978-3-642-36898-1.
18. Hu, MC; Hwang, FK; Wang, Ju Kwei (junio de 1981). "Un problema de límites para pruebas de grupo". Revista SIAM sobre métodos algebraicos y discretos . 2 (2): 81–87. doi :10.1137/0602011.
19. Leu, Ming-Guang (28 de octubre de 2008). "Una nota sobre la conjetura de Hu–Hwang–Wang para pruebas de grupo". The ANZIAM Journal . 49 (4): 561. doi : 10.1017/S1446181108000175 .
20. Riccio, Laura; Colbourn, Charles J. (1 de enero de 2000). "Límites más precisos en pruebas de grupo adaptativas". Revista taiwanesa de matemáticas . 4 (4): 669–673. doi : 10.11650/twjm/1500407300 .
21. Aldridge, Matthew; Baldassini, Leonardo; Johnson, Oliver (junio de 2014). "Algoritmos de prueba grupal: límites y simulaciones". IEEE Transactions on Information Theory . 60 (6): 3671–3687. arXiv : 1306.6438 . doi :10.1109/TIT.2014.2314472. S2CID  8885619.
22. Baldassini, L.; Johnson, O.; Aldridge, M. (1 de julio de 2013), "2013 IEEE International Symposium on Information Theory", IEEE International Symposium on Information Theory , págs. 2676–2680, arXiv : 1301.7023 , CiteSeerX 10.1.1.768.8924 , doi : 10.1109/ISIT.2013.6620712, ISBN  978-1-4799-0446-4, Número de identificación del S2C  9987210
23. Sobel, Milton; Elashoff, RM (1975). "Pruebas grupales con un nuevo objetivo, la estimación". Biometrika . 62 (1): 181–193. doi :10.1093/biomet/62.1.181. hdl : 11299/199154 ​​.
24. Brust, D.; Brust, JJ (enero de 2023). "Diseños de matrices eficaces para pruebas grupales de COVID-19". BMC Bioinformatics . 24 (26): 26. doi : 10.1186/s12859-023-05145-y . PMC 9872308 . PMID  36694117. 
25. Bar-Noy, A.; Hwang, FK; Kessler, I.; Kutten, S. (1 de mayo de 1992). "Un nuevo algoritmo competitivo para pruebas de grupo". [Actas] IEEE INFOCOM '92: La conferencia sobre comunicaciones informáticas . Vol. 2. págs. 786–793. doi :10.1109/INFCOM.1992.263516. ISBN 978-0-7803-0602-8.S2CID16131063  .​
26. Damaschke, Peter (2000). "Aprendizaje adaptativo versus no adaptativo con eficiencia de atributos". Aprendizaje automático . 41 (2): 197–215. doi : 10.1023/A:1007616604496 .
27. Stinson, DR; van Trung, Tran; Wei, R (mayo de 2000). "Códigos seguros a prueba de marcos, patrones de distribución de claves, algoritmos de prueba de grupo y estructuras relacionadas". Revista de planificación e inferencia estadística . 86 (2): 595–617. CiteSeerX 10.1.1.54.6212 . doi :10.1016/S0378-3758(99)00131-7. 
28. Colbourn, CJ; Dinitz, JH; Stinson, DR (1999). "Comunicaciones, criptografía y redes". Encuestas en combinatoria . 3 (267): 37–41. doi : 10.1007/BF01609873 . S2CID  10128581.
29. Goodrich, Michael T.; Atallah, Mikhail J.; Tamassia, Roberto (2005). "Indexación de información para análisis forense de datos". Criptografía aplicada y seguridad de redes . Apuntes de clase en informática. Vol. 3531. págs. 206–221. CiteSeerX 10.1.1.158.6036 . doi :10.1007/11496137_15. ISBN .  978-3-540-26223-7.
30. Chlebus, BS (2001). "Comunicación aleatoria en redes de radio". En Pardalos, PM; Rajasekaran, S.; Reif, J.; Rolim, JDP (eds.). Manual de computación aleatoria . Kluwer Academic. págs. 401–456. ISBN. 978-0-7923-6957-8.
31. Takhar, D.; Laska, JN; Wakin, MB; Duarte, MF; Baron, D.; Sarvotham, S.; Kelly, KF; Baraniuk, RG (febrero de 2006). Bouman, Charles A.; Miller, Eric L.; Pollak, Ilya (eds.). "Una nueva arquitectura de cámara de imágenes compresivas que utiliza compresión de dominio óptico". Imágenes electrónicas . Imágenes computacionales IV. 6065 : 606509–606509–10. Bibcode :2006SPIE.6065...43T. CiteSeerX 10.1.1.114.7872 . doi :10.1117/12.659602. S2CID  7513433. 
32. Candès, EJ (2014). "Matemáticas de la escasez (y algunas otras cosas)". Actas del Congreso Internacional de Matemáticos. Seúl, Corea del Sur .
33. Gilbert, AC; Iwen, MA; Strauss, MJ (octubre de 2008). "Pruebas grupales y recuperación de señales dispersas". 42.ª Conferencia Asilomar sobre señales, sistemas y computadoras . Instituto de Ingenieros Eléctricos y Electrónicos. págs. 1059–63. doi :10.1109/ACSSC.2008.5074574. ISBN 978-1-4244-2940-0.
34. Wright, SJ; Nowak, RD; Figueiredo, MAT (julio de 2009). "Reconstrucción dispersa mediante aproximación separable". IEEE Transactions on Signal Processing . 57 (7): 2479–2493. Bibcode :2009ITSP...57.2479W. CiteSeerX 10.1.1.142.749 . doi :10.1109/TSP.2009.2016892. S2CID  7399917. 
35. Berinde, R.; Gilbert, AC; Indyk, P.; Karloff, H.; Strauss, MJ (septiembre de 2008). "Combinación de geometría y combinatoria: un enfoque unificado para la recuperación de señales dispersas". 2008 46th Annual Allerton Conference on Communication, Control, and Computing . págs. 798–805. arXiv : 0804.4666 . doi :10.1109/ALLERTON.2008.4797639. ISBN 978-1-4244-2925-7. Número de identificación del sujeto  8301134.
36. Indyk, Piotr (1 de enero de 2008). "Construcciones explícitas para la detección comprimida de señales dispersas". Actas del decimonoveno simposio anual ACM-SIAM sobre algoritmos discretos : 30–33.
37. Austin, David. "Columna destacada de AMS: estrategias de agrupación para las pruebas de COVID-19". Sociedad Matemática Estadounidense . Consultado el 3 de octubre de 2020 .
38. Prasanna, Dheeraj. "Agrupación de tapices". tapestry-pooling.herokuapp.com . Consultado el 3 de octubre de 2020 .
39. Chiani, M.; Liva, G.; Paolini, E. (febrero de 2022), "Protocolos de pruebas grupales de identificación y detección para COVID-19 en alta prevalencia", Scientific Reports , 12 (1), Springer Nature: 3250, arXiv : 2104.11305 , Bibcode :2022NatSR..12.3250C, doi : 10.1038/s41598-022-07205-4 , PMC 8885674 , PMID  35228579, S2CID  233387831 
40. "Ensayos de origami". Ensayos de origami. 2 de abril de 2020. Consultado el 7 de abril de 2020 .
41. "Ensayos de origami". Ensayos de origami. 2 de abril de 2020. Consultado el 7 de abril de 2020 .

Referencias generales

• Ding-Zhu, Du; Hwang, Frank K. (1993). Pruebas de grupos combinatorios y sus aplicaciones . Singapur: World Scientific. ISBN 978-9810212933.
• Curso de Atri Rudra sobre Códigos de corrección de errores: combinatoria, algoritmos y aplicaciones (primavera de 2007), conferencias 7.
• Curso de Atri Rudra sobre códigos de corrección de errores: combinatoria, algoritmos y aplicaciones (primavera de 2010), conferencias 10, 11, 28 y 29
• Du, D.; Hwang, F. (2006). Diseños de agrupación y pruebas grupales no adaptativas. World Scientific. ISBN 9789814477864.
• Aldridge, M.; Johnson, O.; Scarlett, J. (2019). "Pruebas grupales: una perspectiva desde la teoría de la información" (PDF) . Fundamentos y tendencias en la teoría de la información y las comunicaciones . 15 (3–4): 196–392. doi :10.1561/0100000099. S2CID  62841593.
• Porat, E.; Rothschild, A. (2011). "Esquemas de prueba de grupos combinatorios no adaptativos explícitos". IEEE Transactions on Information Theory . 57 (12): 7982–89. arXiv : 0712.3876 . doi :10.1109/TIT.2011.2163296. S2CID  8815474.
• Kagan, Eugene; Ben-gal, Irad (2014), "Un algoritmo de prueba grupal con aprendizaje informativo en línea", IIE Transactions , 46 (2): 164–184, doi :10.1080/0740817X.2013.803639, ISSN  0740-817X, S2CID  18588494

Véase también

• Rompecabezas de equilibrio