En geometría , un politopo truncado de 24 celdas es un politopo uniforme de 4 dimensiones ( politopo uniforme de 4 dimensiones ) formado como el truncamiento del politopo regular de 24 celdas .
Hay dos grados de truncamiento, incluido un truncamiento de bits .
El icositetracoron truncado de 24 celdas o icositetracoron truncado es un politopo uniforme de 4 dimensiones (o 4-politopo uniforme ), que está limitado por 48 celdas : 24 cubos y 24 octaedros truncados . Cada vértice une tres octaedros truncados y un cubo, en una figura de vértice de pirámide triangular equilátera .
El sistema truncado de 24 celdas se puede construir a partir de politopos con tres grupos de simetría:
También es un zonotopo : puede formarse como la suma de Minkowski de los seis segmentos de línea que conectan pares opuestos entre las doce permutaciones del vector (+1,−1,0,0).
Las coordenadas cartesianas de los vértices de una celda truncada de 24 celdas que tiene una longitud de arista sqrt(2) son todas permutaciones de coordenadas y combinaciones de signos de:
La configuración dual tiene coordenadas en todas las permutaciones de coordenadas y signos de
Las 24 celdas cúbicas están unidas a través de sus caras cuadradas a los octaedros truncados; y los 24 octaedros truncados están unidos entre sí a través de sus caras hexagonales.
La proyección paralela del octaedro truncado de 24 celdas en el espacio tridimensional, primero el octaedro truncado, tiene la siguiente disposición:
La envoltura convexa del policoron truncado de 24 celdas y su dual (asumiendo que son congruentes) es un policoron no uniforme compuesto de 480 celdas: 48 cubos , 144 antiprismas cuadrados , 288 tetraedros (como disfenoides tetragonales) y 384 vértices. Su figura de vértice es una cúpula hexakis triangular .
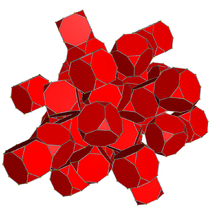
El bitruncado de 24 células . 48 células , o tetracontoctachoron es un politopo uniforme de 4 dimensiones (o 4-politopo uniforme ) derivado del de 24 células .
EL Elte lo identificó en 1912 como un politopo semirregular.
Se construye truncando las 24 celdas (truncando a la mitad de la profundidad, lo que daría como resultado las 24 celdas duales ).
Al ser un politopo cuatridimensional uniforme, es transitivo por vértices . Además, es transitivo por celdas , ya que consta de 48 cubos truncados , y también transitivo por aristas , con 3 celdas de cubos truncados por arista y con un triángulo y dos octógonos alrededor de cada arista.
Las 48 celdas del sistema bitruncado de 24 celdas se corresponden con las 24 celdas y los 24 vértices del sistema de 24 celdas. Por lo tanto, los centros de las 48 celdas forman el sistema de raíces del tipo F 4 .
Su figura de vértice es un difenoide tetragonal , un tetraedro con 2 aristas opuestas de longitud 1 y las 4 aristas laterales de longitud √(2+√2).
Los cubos truncados están unidos entre sí a través de sus caras octogonales en orientación anti ; es decir, dos cubos truncados contiguos se giran 45 grados uno con respecto al otro de modo que ninguna de las caras triangulares comparta una arista.
La secuencia de cubos truncados unidos entre sí por caras octogonales opuestas forma un ciclo de 8. Cada cubo truncado pertenece a 3 de estos ciclos. Por otro lado, la secuencia de cubos truncados unidos entre sí por caras triangulares opuestas forma un ciclo de 6. Cada cubo truncado pertenece a 4 de estos ciclos.
Visto en una matriz de configuración , se muestran todos los recuentos de incidencia entre elementos. Los números del f-vector diagonal se derivan a través de la construcción de Wythoff , dividiendo el orden de grupo completo de un orden de subgrupo eliminando un espejo a la vez. Los bordes existen en 4 posiciones de simetría. Los cuadrados existen en 3 posiciones, los hexágonos en 2 posiciones y los octógonos en una. Finalmente, los 4 tipos de celdas existen centrados en las 4 esquinas del símplex fundamental. [1]
Las coordenadas cartesianas de un sistema de 24 celdas bitruncado que tiene una longitud de arista de 2 son todas permutaciones de coordenadas y signo de:
El poliedro oblicuo regular , {8,4|3}, existe en el espacio 4 con 4 caras octogonales alrededor de cada vértice, en una figura de vértice no plana en zigzag. Estas caras octogonales se pueden ver en la figura de 24 celdas bitruncada, utilizando las 576 aristas y los 288 vértices. Las 192 caras triangulares de la figura de 24 celdas bitruncada se pueden ver eliminadas. El poliedro oblicuo regular dual, {4,8|3}, está relacionado de manera similar con las caras cuadradas de la figura de 24 celdas runcinada .
El politopo de 288 celdas es el dual del politopo bitruncado de 24 celdas. Es un politopo de 4 dimensiones (o policorono ) derivado del politopo de 24 celdas . Se construye duplicando y rotando el politopo de 24 celdas y luego construyendo la envoltura convexa .
Al ser el dual de un policoron uniforme, es transitivo a nivel celular y consta de 288 difenoides tetragonales congruentes . Además, es transitivo a nivel de vértice bajo el grupo Aut(F 4 ). [3]
Los vértices de la celda 288 son precisamente los 24 cuaterniones unitarios de Hurwitz con norma al cuadrado 1, unidos con los 24 vértices de la celda dual 24 con norma al cuadrado 2, proyectados a la esfera unitaria 3. Estos 48 vértices corresponden al grupo octaédrico binario 2O o <2,3,4>, de orden 48.
Así, el de 288 celdas es el único 4-politopo no regular que es la envoltura convexa de un grupo cuaterniónico, sin tener en cuenta los infinitos grupos dicíclicos (igual que el grupo diedro binario); los regulares son el de 24 celdas (≘ 2T o <2,3,3>, orden 24) y el de 600 celdas (≘ 2I o <2,3,5>, orden 120). (El de 16 celdas corresponde al grupo diedro binario 2D 2 o <2,2,2>, orden 16.)
La 3-esfera inscrita tiene un radio de 1/2+ √ 2 /4 ≈ 0,853553 y toca la celda 288 en los centros de los 288 tetraedros que son los vértices de la celda 24 bitruncada dual.
Los vértices se pueden colorear de dos colores , por ejemplo, rojo y amarillo, con las 24 unidades de Hurwitz en rojo y los 24 duales en amarillo, siendo la celda amarilla de 24 congruente con la roja. Por lo tanto, el producto de dos cuaterniones de igual color es rojo y el producto de dos en colores mezclados es amarillo.
Colocando un vértice rojo fijo en el polo norte (1,0,0,0), hay 6 vértices amarillos en la siguiente “latitud” más profunda en ( √ 2 /2,x,y,z), seguidos de 8 vértices rojos en la latitud en (1/2,x,y,z). Las coordenadas completas se dan como combinaciones lineales de las unidades cuaterniónicas , que al mismo tiempo pueden tomarse como los elementos del grupo 2O . La siguiente latitud más profunda es el hiperplano del ecuador que interseca la 3-esfera en una 2-esfera que está poblada por 6 vértices rojos y 12 amarillos.
La capa 2 es una esfera de 2 lados que circunscribe un octaedro regular cuyas aristas tienen una longitud de 1. Un tetraedro con un vértice en el polo norte tiene una de estas aristas como arista larga cuyos 2 vértices están conectados por aristas cortas al polo norte. Otra arista larga va desde el polo norte hacia la capa 1 y 2 aristas cortas desde allí hacia la capa 2 .
Hay 192 aristas largas con longitud 1 que unen colores iguales y 144 aristas cortas con longitud √ 2– √ 2 ≈ 0,765367 que unen colores mezclados. 192*2/48 = 8 de largo y 144*2/48 = 6 cortos, es decir, en conjunto 14 aristas se encuentran en cualquier vértice.
Las 576 caras son isósceles con una arista larga y dos cortas, todas congruentes. Los ángulos en la base son arccos( √ 4+ √ 8 /4) ≈ 49,210°. 576*3/48 = 36 caras se encuentran en un vértice, 576*1/192 = 3 en una arista larga y 576*2/144 = 8 en una corta.
Las 288 celdas son tetraedros con 4 aristas cortas y 2 aristas largas antípodas y perpendiculares, una de las cuales conecta 2 vértices rojos y los otros 2 amarillos. Todas las celdas son congruentes. 288*4/48 = 24 celdas se unen en un vértice. 288*2/192 = 3 celdas se unen en una arista larga, 288*4/144 = 8 en una corta. 288*4/576 = 2 celdas se unen en un triángulo.
B 4 familia de politopos uniformes:
Familia F 4 de politopos uniformes: