Función hash perfecta

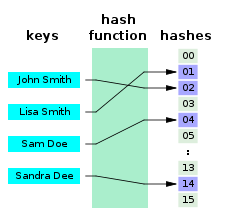
En informática , una función hash perfecta $h$ para un conjunto $S$ es una función hash que asigna elementos distintos de $S$ a un conjunto de $m$ enteros, sin colisiones . En términos matemáticos, es una función inyectiva .

Las funciones hash perfectas se pueden utilizar para implementar una tabla de búsqueda con un tiempo de acceso constante en el peor de los casos. Una función hash perfecta se puede utilizar , como cualquier función hash , para implementar tablas hash , con la ventaja de que no se debe implementar ninguna resolución de colisiones . Además, si las claves no están en los datos y se sabe que las claves consultadas serán válidas, no es necesario almacenarlas en la tabla de búsqueda, lo que ahorra espacio.

Las desventajas de las funciones hash perfectas son que se debe conocer $S$ para la construcción de la función hash perfecta. Las funciones hash perfectas no dinámicas deben reconstruirse si $S$ cambia. Para $S que cambia con frecuencia, se pueden usar$ funciones hash perfectas dinámicas a costa de espacio adicional. ^[1] El requisito de espacio para almacenar la función hash perfecta es en $O (n)$ donde $n$ es el número de claves en la estructura.

Los parámetros de rendimiento importantes para las funciones hash perfectas son el tiempo de evaluación, que debe ser constante, el tiempo de construcción y el tamaño de representación.

Solicitud

Una función hash perfecta con valores en un rango limitado puede utilizarse para operaciones de búsqueda eficientes, colocando claves de $S$ (u otros valores asociados) en una tabla de búsqueda indexada por la salida de la función. Luego, se puede comprobar si una clave está presente en $S$ , o buscar un valor asociado con esa clave, buscándolo en su celda de la tabla. Cada una de esas búsquedas lleva un tiempo constante en el peor de los casos . ^[2] Con un hash perfecto, los datos asociados se pueden leer o escribir con un solo acceso a la tabla. ^[3]

Rendimiento de funciones hash perfectas

Los parámetros de rendimiento importantes para un hash perfecto son el tamaño de la representación, el tiempo de evaluación, el tiempo de construcción y, además, el requisito de rango (número promedio de contenedores por clave en la tabla hash). ^[4] El tiempo de evaluación puede ser tan rápido como $O$ $($ $1$ $)$ , lo cual es óptimo. ^[2]^[4] El tiempo de construcción debe ser al menos $O$ $($ $n$ $)$ , porque cada elemento en $S$ necesita ser considerado, y $S$ contiene $n$ elementos. Este límite inferior se puede lograr en la práctica. ^[4] ${\frac {m}{n}}$

El límite inferior para el tamaño de la representación depende de $m$ y $n$ . Sea $m = (1+ε) n$ y $h$ una función hash perfecta. Una buena aproximación para el límite inferior es Bits por elemento. Para un hash perfecto mínimo, $ε = 0$ , el límite inferior es $log e \approx 1,44$ bits por elemento. ^[4] $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$

Construcción

Una función hash perfecta para un conjunto específico $S$ que se puede evaluar en tiempo constante, y con valores en un rango pequeño, se puede encontrar mediante un algoritmo aleatorio en un número de operaciones que es proporcional al tamaño de S. La construcción original de Fredman, Komlós y Szemerédi (1984) utiliza un esquema de dos niveles para mapear un conjunto $S$ de $n$ elementos a un rango de índices $O (n)$ y luego mapear cada índice a un rango de valores hash. El primer nivel de su construcción elige un primo grande $p$ (más grande que el tamaño del universo del cual se extrae $S$ ), y un parámetro $k$ , y mapea cada elemento $x$ de $S$ al índice

g(x)=(kx{\bmod {p}}){\bmod {n}}.

Si $k$ se elige aleatoriamente, es probable que este paso tenga colisiones, pero es probable que el número de elementos $n i$ que se asignan simultáneamente al mismo índice $i$ sea pequeño. El segundo nivel de su construcción asigna rangos disjuntos de $O (n i 2)$ enteros a cada índice $i$ . Utiliza un segundo conjunto de funciones modulares lineales, una para cada índice $i$ , para asignar cada miembro $x$ de $S$ al rango asociado con $g (x)$ . ^[2]

Como muestran Fredman, Komlós y Szemerédi (1984), existe una elección del parámetro $k$ tal que la suma de las longitudes de los rangos para los $n$ valores diferentes de $g (x)$ sea $O (n)$ . Además, para cada valor de $g (x)$ , existe una función modular lineal que mapea el subconjunto correspondiente de $S$ en el rango asociado con ese valor. Tanto $k$ como las funciones de segundo nivel para cada valor de $g (x)$ , se pueden encontrar en tiempo polinomial eligiendo valores aleatoriamente hasta encontrar uno que funcione. ^[2]

La función hash en sí misma requiere espacio de almacenamiento $O (n)$ para almacenar $k$ , $p$ y todas las funciones modulares lineales de segundo nivel. El cálculo del valor hash de una clave dada $x$ se puede realizar en tiempo constante calculando $g (x)$ , buscando la función de segundo nivel asociada con $g (x)$ y aplicando esta función a $x$ . Se puede utilizar una versión modificada de este esquema de dos niveles con una mayor cantidad de valores en el nivel superior para construir una función hash perfecta que mapee $S$ en un rango más pequeño de longitud $n + o (n)$ . ^[2]

Belazzougui, Botelho y Dietzfelbinger (2009) describen un método más reciente para construir una función hash perfecta como "hash, desplazamiento y compresión". Aquí también se utiliza una función hash de primer nivel $g para mapear elementos en un rango de números enteros$ $r$ . Un elemento $x \in S$ se almacena en el contenedor $B g(x)$ . ^[4]

Luego, en orden descendente de tamaño, los elementos de cada contenedor se codifican mediante una función hash de una secuencia de funciones hash independientes completamente aleatorias $(Φ 1, Φ 2, Φ 3, ...)$ , comenzando con $Φ 1$ . Si la función hash no produce ninguna colisión para el contenedor, y los valores resultantes aún no están ocupados por otros elementos de otros contenedores, se elige la función para ese contenedor. Si no, se prueba la siguiente función hash en la secuencia. ^[4]

Para evaluar la función hash perfecta $h (x)$ solo hay que guardar la asignación σ del índice de cubo $g (x)$ en la función hash correcta en la secuencia, lo que da como resultado $h(x) = Φ σ(g(x))$ . ^[4]

Finalmente, para reducir el tamaño de la representación, los ( $σ(i)) 0 \leq i < r$ se comprimen en una forma que aún permite la evaluación en $O (1)$ . ^[4]

Este enfoque necesita un tiempo lineal en $n$ para la construcción y un tiempo de evaluación constante. El tamaño de la representación está en $O (n)$ y depende del rango alcanzado. Por ejemplo, con $m = 1,23 n,$ Belazzougui, Botelho y Dietzfelbinger (2009) lograron un tamaño de representación entre 3,03 bits/clave y 1,40 bits/clave para su conjunto de ejemplo dado de 10 millones de entradas, y los valores más bajos necesitan un mayor tiempo de cálculo. El límite inferior del espacio en este escenario es 0,88 bits/clave. ^[4]

Pseudocódigo

El algoritmo  hash, desplazar y comprimir  es
(1) Dividir S en grupos  $B i := g -1 ({i})\capS,0 \leq i < r$ 
(2) Ordenar los grupos B _i en orden descendente según el tamaño |B _i |(3) Inicializar la matriz T[0...m-1] con 0(4) para todo i  ∈[r], en el orden de (2), haga
(5) para l  ←  1,2,...(6) repetir la formación de K _i  ←  {  $Φ$ _l (x)|x  ∈  B _i }(6) hasta que |K _i |=|B _i | y K _i ∩{j|T[j]=1}=  ∅(7) sea σ(i):= el l exitoso(8) para todo j  ∈  K _i sea T[j]:=  1(9) Transforme (σ _i ) _0≤i<r en forma comprimida, conservando el acceso  $O (1)$  .

Límites inferiores del espacio

El uso de $O (n)$ palabras de información para almacenar la función de Fredman, Komlós y Szemerédi (1984) es casi óptimo: cualquier función hash perfecta que pueda calcularse en tiempo constante requiere al menos un número de bits que sea proporcional al tamaño de $S.$ ^[5 ]

Para funciones hash mínimas perfectas, el límite inferior del espacio teórico de la información es

\log _{2}e\aproximadamente 1,44

bits/llave. ^[4]

Para funciones hash perfectas, primero se supone que el rango de $h$ está acotado por $n$ como $m = (1+ε) n$ . Con la fórmula dada por Belazzougui, Botelho y Dietzfelbinger (2009) y para un universo cuyo tamaño $|$ $U$ $| =$ $u$ tiende hacia el infinito, los límites inferiores del espacio son $U\supseteq S$

\log _{2}e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}

bits/clave, menos $log(n)$ bits en total. ^[4]

Extensiones

Identidad de la dirección de memoria

Un ejemplo trivial pero generalizado de hash perfecto está implícito en el espacio de direcciones de memoria (virtual) de una computadora. Dado que cada byte de memoria virtual es una ubicación de almacenamiento distinta, única y directamente direccionable, el valor de la dirección inicial donde se almacena cualquier objeto en la memoria puede considerarse un hash perfecto de facto de ese objeto en todo el rango de direcciones de memoria. ^[6]

Hashing perfecto dinámico

El uso de una función hash perfecta es mejor en situaciones en las que hay un conjunto grande, $S$ , que se consulta con frecuencia y que rara vez se actualiza. Esto se debe a que cualquier modificación del conjunto $S$ puede hacer que la función hash ya no sea perfecta para el conjunto modificado. Las soluciones que actualizan la función hash cada vez que se modifica el conjunto se conocen como hash perfecto dinámico ^[1] , pero estos métodos son relativamente complicados de implementar.

Función hash mínima perfecta

Una función hash mínima perfecta es una función hash perfecta que asigna $n$ claves a $n$ enteros consecutivos, generalmente los números de $0$ a $n - 1$ o de $1$ a $n$ . Una forma más formal de expresar esto es: Sean $j$ y $k$ elementos de algún conjunto finito $S$ . Entonces $h$ es una función hash mínima perfecta si y solo si $h (j) = h (k)$ implica $j = k$ ( inyectividad ) y existe un entero $a$ tal que el rango de $h$ es $a .. a + | S | - 1$ . Se ha demostrado que un esquema hash mínimo perfecto de propósito general requiere al menos bits/clave. ^[4] Suponiendo que es un conjunto de tamaño que contiene enteros en el rango , se sabe cómo construir eficientemente una función hash mínima perfecta explícita de a que usa bits espaciales y que admite un tiempo de evaluación constante. ^[7] En la práctica, hay esquemas hash mínimos perfectos que usan aproximadamente 1,56 bits/clave si se les da suficiente tiempo. ^[8] $\log _{2}e\aproximadamente 1,44$ ${\estilo de visualización S}$ ${\estilo de visualización n}$ $[1,2^{o(n)}]$ ${\estilo de visualización S}$ $\{1,2,\lpuntos ,n\}$ $n\log _{2}e+o(n)$

Hashing k-perfecto

Una función hash es $k$ -perfecta si, como máximo, $k$ elementos de $S$ se asignan al mismo valor en el rango. El algoritmo "hash, desplazamiento y compresión" se puede utilizar para construir funciones hash $k$ -perfectas permitiendo hasta $k$ colisiones. Los cambios necesarios para lograr esto son mínimos y se subrayan en el pseudocódigo adaptado que aparece a continuación:

(4) para todo i  ∈[r], en el orden de (2), haga
(5) para l  ←  1,2,...(6) repetir la formación de K _i  ←  {  $Φ$ _l (x)|x  ∈  B _i }(6) hasta que |K _i |=|B _i | y K _i ∩{j| T[j]=k }=  ∅(7) sea σ(i):= el l exitoso(8) para todo j  ∈  K _i establece  T[j]←T[j]+1

Conservación del orden

Una función hash mínima perfecta $F$ preserva el orden si las claves se dan en algún orden $a 1, a 2, ..., a n$ y para cualquier clave $a j$ y $a k$ , $j < k$ implica $F (a j) < F(a k)$ . ^[9] En este caso, el valor de la función es simplemente la posición de cada clave en el orden ordenado de todas las claves. Una implementación simple de funciones hash mínimas perfectas que preservan el orden con un tiempo de acceso constante es usar una función hash perfecta (ordinaria) para almacenar una tabla de búsqueda de las posiciones de cada clave. Esta solución usa bits, lo cual es óptimo en el entorno donde la función de comparación para las claves puede ser arbitraria. ^[10] Sin embargo, si las claves $a$ $1$ $,$ $a$ $2$ $, ...,$ $a$ $n$ son números enteros extraídos de un universo , entonces es posible construir una función hash que preserve el orden usando solo bits de espacio. ^[11] Además, se sabe que este límite es óptimo. ^[12] $O(n\log n)$ $\{1,2,\ldots ,U\}$ $O(n\log \log \log U)$

Construcciones relacionadas

Si bien las tablas hash bien dimensionadas tienen un tiempo O(1) promedio amortizado (tiempo constante promedio amortizado) para búsquedas, inserciones y eliminación, la mayoría de los algoritmos de tablas hash sufren posibles tiempos en el peor de los casos que toman mucho más tiempo. Un tiempo O(1) en el peor de los casos (tiempo constante incluso en el peor de los casos) sería mejor para muchas aplicaciones (incluidos los enrutadores de red y las memorias caché ). ^[13]^{: 41}

Pocos algoritmos de tabla hash admiten un tiempo de búsqueda O(1) en el peor de los casos (tiempo de búsqueda constante incluso en el peor de los casos). Los pocos que lo hacen incluyen: hash perfecto; hash perfecto dinámico ; hash cuckoo ; hash hopscotch ; y hash extensible . ^[13]^{: 42–69}

Una alternativa sencilla al hash perfecto, que también permite actualizaciones dinámicas, es el hash cuckoo . Este esquema asigna claves a dos o más ubicaciones dentro de un rango (a diferencia del hash perfecto que asigna cada clave a una sola ubicación), pero lo hace de tal manera que las claves se pueden asignar una a una a las ubicaciones a las que han sido asignadas. Las búsquedas con este esquema son más lentas, porque se deben verificar múltiples ubicaciones, pero sin embargo toman un tiempo constante en el peor de los casos. ^[14]

Referencias

^ ab Dietzfelbinger, Martín; Karlín, Anna ; Mehlhorn, Kurt ; Meyer auf der Heide, Friedhelm; Rohnert, Hans; Tarjan, Robert E. (1994), "Hashing dinámico perfecto: límites superior e inferior", SIAM Journal on Computing , 23 (4): 738–761, doi :10.1137/S0097539791194094, MR 1283572.
^ abcde Fredman, Michael L .; Komlós, János ; Szemerédi, Endre (1984), "Almacenamiento de una tabla dispersa con $O$ $(1)$ tiempo de acceso en el peor de los casos", Journal of the ACM , 31 (3): 538, doi : 10.1145/828.1884 , MR 0819156, S2CID 5399743
^ Lu, Yi; Prabhakar, Balaji; Bonomi, Flavio (2006), "Hash perfecto para aplicaciones de red", Simposio internacional IEEE sobre teoría de la información de 2006 , págs. 2774-2778, doi :10.1109/ISIT.2006.261567, ISBN 1-4244-0505-X, Número de identificación del sujeto 1494710
^ abcdefghijkl Belazzougui, Djamal; Botelho, Fabiano C.; Dietzfelbinger, Martin (2009), "Hash, desplazar y comprimir" (PDF) , Algoritmos - ESA 2009 (PDF) , Lecture Notes in Computer Science , vol. 5757, Berlín: Springer, págs. 682–693, CiteSeerX 10.1.1.568.130 , doi :10.1007/978-3-642-04128-0_61, ISBN 978-3-642-04127-3, Sr. 2557794.
^ Fredman, Michael L. ; Komlós, János (1984), "Sobre el tamaño de los sistemas de separación y familias de funciones hash perfectas", SIAM Journal on Algebraic and Discrete Methods , 5 (1): 61–68, doi :10.1137/0605009, MR 0731857.
^ Witold Litwin; Tadeusz Morzy; Gottfried Vossen (19 de agosto de 1998). Avances en bases de datos y sistemas de información. Springer Science+Business Media . p. 254. ISBN 9783540649243.
^ Hagerup, Torben; Tholey, Torsten (2001), "Hash perfecto mínimo eficiente en un espacio casi mínimo", STACS 2001 , Berlín, Heidelberg: Springer Berlin Heidelberg, págs. 317–326, doi :10.1007/3-540-44693-1_28, ISBN 978-3-540-41695-1, consultado el 12 de noviembre de 2023
^ Esposito, Emmanuel; Mueller Graf, Thomas; Vigna, Sebastiano (2020), "RecSplit: Hashing perfecto mínimo a través de división recursiva", Actas del Simposio sobre ingeniería de algoritmos y experimentos (ALENEX) de 2020 , Actas , págs. 175–185, arXiv : 1910.06416 , doi : 10.1137/1.9781611976007.14.
^ Jenkins, Bob (14 de abril de 2009), "order-preserving minimal perfect hashing", en Black, Paul E. (ed.), Dictionary of Algorithms and Data Structures, Instituto Nacional de Estándares y Tecnología de EE. UU. , consultado el 5 de marzo de 2013
^ Fox, Edward A.; Chen, Qi Fan; Daoud, Amjad M.; Heath, Lenwood S. (julio de 1991), "Funciones hash perfectas mínimas que preservan el orden y recuperación de información" (PDF) , ACM Transactions on Information Systems , 9 (3), Nueva York, NY, EE. UU.: ACM: 281–308, doi :10.1145/125187.125200, S2CID 53239140.
^ Belazzougui, Djamal; Boldi, Paolo; Pagh, Rasmus ; Vigna, Sebastiano (noviembre de 2008), "Teoría y práctica del hash mínimo perfecto monótono", Journal of Experimental Algorithmics , 16 , Art. no. 3.2, 26pp, doi :10.1145/1963190.2025378, S2CID 2367401.
^ Assadi, Sepehr; Farach-Colton, Martín; Kuszmaul, William (enero de 2023), "Límites estrictos para el hash perfecto mínimo monótono", Actas del Simposio anual ACM-SIAM de 2023 sobre algoritmos discretos (SODA) , Filadelfia, PA: Society for Industrial and Applied Mathematics, págs. 456–476, arXiv : 2207.10556 , doi : 10.1137/1.9781611977554.ch20, ISBN 978-1-61197-755-4, consultado el 27 de abril de 2023
^ de Timothy A. Davis. "Capítulo 5 Hashing": subsección "Tablas hash con acceso O(1) en el peor de los casos"
^ Pagh, Rasmus ; Rodler, Flemming Friche (2004), "Cuckoo hash", Journal of Algorithms , 51 (2): 122–144, doi :10.1016/j.jalgor.2003.12.002, MR 2050140.

Lectura adicional

Richard J. Cichelli. Funciones hash mínimas perfectas simplificadas , Communications of the ACM, vol. 23, número 1, enero de 1980.
Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest y Clifford Stein . Introducción a los algoritmos , tercera edición. MIT Press, 2009. ISBN 978-0262033848 . Sección 11.5: Hashing perfecto, págs. 267, 277–282.
Fabiano C. Botelho, Rasmus Pagh y Nivio Ziviani. "Hashing perfecto para aplicaciones de gestión de datos".
Fabiano C. Botelho y Nivio Ziviani . "Hash externo perfecto para conjuntos de claves muy grandes". 16ª Conferencia ACM sobre Gestión de la Información y el Conocimiento (CIKM07), Lisboa, Portugal, noviembre de 2007.
Djamal Belazzougui, Paolo Boldi, Rasmus Pagh y Sebastiano Vigna. "Hash minimalista perfecto monótono: búsqueda en una tabla ordenada con accesos O(1)". En Actas del 20.º Simposio Anual ACM-SIAM sobre Matemáticas Discretas (SODA), Nueva York, 2009. ACM Press.
Marshall D. Brain y Alan L. Tharp. "Near-perfect Hashing of Large Word Sets" (Hash casi perfecto de grandes conjuntos de palabras). Software—Practice and Experience, vol. 19(10), 967-078, octubre de 1989. John Wiley & Sons.
Douglas C. Schmidt, GPERF: un generador de funciones hash perfecto, C++ Report, SIGS, vol. 10, n.º 10, noviembre/diciembre de 1998.

Enlaces externos

gperf es un generador de hash perfecto de código abierto para C y C++ (muy rápido, pero solo funciona para conjuntos pequeños)
Algoritmo Bob (hashing mínimo perfecto) de Bob Jenkins
cmph: Biblioteca de hashes perfectos mínimos de C, implementaciones de código abierto para muchos hashes perfectos (mínimos) (funciona para conjuntos grandes)
Sux4J: algoritmo hash minimalista perfecto y monótono de código abierto en Java
MPHSharp: métodos hash perfectos en C#
BBHash: función hash perfecta mínima en C++ con solo encabezado
Perfect::Hash, generador de hash perfecto en Perl que genera código C. Tiene una sección de "estado de la técnica" que vale la pena consultar.