Partición de enteros

Descomposición de un número entero como suma de números enteros positivos

Diagramas de Young asociados a las particiones de los números enteros positivos del 1 al 8. Están dispuestos de manera que las imágenes bajo la reflexión sobre la diagonal principal del cuadrado son particiones conjugadas.

Particiones de n con la parte más grande k

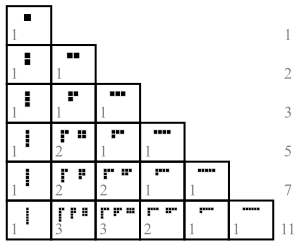
En teoría de números y combinatoria , una partición de un entero no negativo n , también llamada partición entera , es una forma de escribir n como suma de enteros positivos . Dos sumas que difieren solo en el orden de sus sumandos se consideran la misma partición. (Si el orden importa, la suma se convierte en una composición ). Por ejemplo, 4 se puede particionar de cinco formas distintas:

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

La única partición del cero es la suma vacía, que no tiene partes.

La composición dependiente del orden 1 + 3 es la misma partición que 3 + 1 , y las dos composiciones distintas 1 + 2 + 1 y 1 + 1 + 2 representan la misma partición que 2 + 1 + 1 .

Un sumando individual en una partición se llama parte . El número de particiones de n está dado por la función de partición p ( n ) . Por lo tanto, p (4) = 5. La notación λ ⊢ n significa que λ es una partición de n .

Las particiones se pueden visualizar gráficamente con diagramas de Young o diagramas de Ferrers . Se presentan en varias ramas de las matemáticas y la física , incluido el estudio de polinomios simétricos y del grupo simétrico y en la teoría de representación de grupos en general.

Ejemplos

Las siete particiones de 5 son

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

Algunos autores tratan una partición como una secuencia decreciente de sumandos, en lugar de una expresión con signos más. Por ejemplo, la partición 2 + 2 + 1 podría escribirse como la tupla (2, 2, 1) o en la forma aún más compacta (2 ² , 1) donde el superíndice indica el número de repeticiones de una parte.

Esta notación de multiplicidad para una partición se puede escribir alternativamente como , donde m ₁ es el número de 1, m ₂ es el número de 2, etc. (Los componentes con m _i = 0 pueden omitirse). Por ejemplo, en esta notación, las particiones de 5 se escriben , y . ${\displaystyle 1^{m_{1}}2^{m_{2}}3^{m_{3}}\cdots }$ ${\displaystyle 5^{1},1^{1}4^{1},2^{1}3^{1},1^{2}3^{1},1^{1}2^{2},1^{3}2^{1}}$ ${\displaystyle 1^{5}}$

Representaciones diagramáticas de particiones

Existen dos métodos diagramáticos comunes para representar particiones: los diagramas de Ferrers, llamados así por Norman Macleod Ferrers , y los diagramas de Young, llamados así por Alfred Young . Ambos tienen varias convenciones posibles; aquí, usamos la notación inglesa , con los diagramas alineados en la esquina superior izquierda.

Diagrama de Ferrers

La partición 6 + 4 + 3 + 1 del número 14 se puede representar mediante el siguiente diagrama:

Los 14 círculos están alineados en 4 filas, cada una de las cuales tiene el tamaño de una parte de la partición. Los diagramas de las 5 particiones del número 4 se muestran a continuación:

Diagrama joven

Una representación visual alternativa de una partición entera es su diagrama de Young (a menudo también llamado diagrama de Ferrers). En lugar de representar una partición con puntos, como en el diagrama de Ferrers, el diagrama de Young utiliza cajas o cuadrados. Por lo tanto, el diagrama de Young para la partición 5 + 4 + 1 es

mientras que el diagrama de Ferrers para la misma partición es

Aunque esta variación aparentemente trivial no parece digna de mención por separado, los diagramas de Young resultan ser extremadamente útiles en el estudio de funciones simétricas y la teoría de la representación de grupos : llenar las cajas de los diagramas de Young con números (o a veces objetos más complicados) que obedecen varias reglas conduce a una familia de objetos llamados cuadros de Young , y estos cuadros tienen significado combinatorio y teórico de la representación. ^[1] Como un tipo de forma hecha por cuadrados adyacentes unidos entre sí, los diagramas de Young son un tipo especial de poliominó . ^[2]

Función de partición

Utilizando el método de Euler para hallar p (40): Se desliza hacia abajo una regla con signos más y menos (recuadro gris) y se suman o restan las partes correspondientes. Las posiciones de los signos se dan por diferencias de números naturales (azules) e impares (naranjas) alternados. En el archivo SVG, pase el cursor sobre la imagen para mover la regla.

La función de partición cuenta las particiones de un entero no negativo . Por ejemplo, dado que el entero tiene cinco particiones , , , y . Los valores de esta función para son: ${\displaystyle p(n)}$ ${\displaystyle n}$ ${\displaystyle p(4)=5}$ ${\displaystyle 4}$ ${\displaystyle 1+1+1+1}$ ${\displaystyle 1+1+2}$ ${\displaystyle 1+3}$ ${\displaystyle 2+2}$ ${\displaystyle 4}$ ${\displaystyle n=0,1,2,\dots }$

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ... (secuencia A000041 en la OEIS ).

La función generadora de es ${\displaystyle p}$

${\displaystyle \sum _{n=0}^{\infty }p(n)q^{n}=\prod _{j=1}^{\infty }\sum _{i=0}^{\infty }q^{ji}=\prod _{j=1}^{\infty }(1-q^{j})^{-1}.}$

No se conoce ninguna expresión cerrada para la función de partición, pero tiene tanto expansiones asintóticas que la aproximan con precisión como relaciones de recurrencia mediante las cuales se puede calcular con exactitud. Crece como una función exponencial de la raíz cuadrada de su argumento, ^[3] de la siguiente manera:

${\displaystyle p(n)\sim {\frac {1}{4n{\sqrt {3}}}}\exp \left({\pi {\sqrt {\frac {2n}{3}}}}\right)}$como ${\displaystyle n\to \infty }$

En 1937, Hans Rademacher encontró una forma de representar la función de partición mediante la serie convergente. ${\displaystyle p(n)}$

$${\displaystyle p(n)={\frac {1}{\pi {\sqrt {2}}}}\sum _{k=1}^{\infty }A_{k}(n){\sqrt {k}}\cdot {\frac {d}{dn}}\left({{\frac {1}{\sqrt {n-{\frac {1}{24}}}}}\sinh \left[{{\frac {\pi }{k}}{\sqrt {{\frac {2}{3}}\left(n-{\frac {1}{24}}\right)}}}\,\,\,\right]}\right)}$$dónde

$${\displaystyle A_{k}(n)=\sum _{0\leq m<k,\;(m,k)=1}e^{\pi i\left(s(m,k)-2nm/k\right)}.}$$y es la suma de Dedekind . ${\displaystyle s(m,k)}$

La inversa multiplicativa de su función generadora es la función de Euler ; por el teorema del número pentagonal de Euler, esta función es una suma alternada de potencias de números pentagonales de su argumento.

${\displaystyle p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+\cdots }$

Srinivasa Ramanujan descubrió que la función de partición tiene patrones no triviales en la aritmética modular , ahora conocidos como congruencias de Ramanujan . Por ejemplo, siempre que la representación decimal de termine en el dígito 4 o 9, el número de particiones de será divisible por 5. ^[4] ${\displaystyle n}$ ${\displaystyle n}$

Particiones restringidas

Tanto en combinatoria como en teoría de números, a menudo se estudian familias de particiones sujetas a diversas restricciones. ^[5] En esta sección se examinan algunas de esas restricciones.

Particiones conjugadas y autoconjugadas

Si invertimos el diagrama de la partición 6 + 4 + 3 + 1 a lo largo de su diagonal principal, obtenemos otra partición de 14:

Al convertir las filas en columnas, obtenemos la partición 4 + 3 + 3 + 2 + 1 + 1 del número 14. Se dice que tales particiones son conjugadas entre sí. ^[6] En el caso del número 4, las particiones 4 y 1 + 1 + 1 + 1 son pares conjugados, y las particiones 3 + 1 y 2 + 1 + 1 son conjugadas entre sí. De particular interés son las particiones, como 2 + 2, que se tienen a sí mismas como conjugadas. Se dice que tales particiones son autoconjugadas . ^[7]

Afirmación : El número de particiones autoconjugadas es el mismo que el número de particiones con partes impares distintas.

Prueba (esquema) : La observación crucial es que cada parte impar se puede " doblar " por la mitad para formar un diagrama autoconjugado:

Se puede entonces obtener una biyección entre el conjunto de particiones con partes impares distintas y el conjunto de particiones autoconjugadas, como lo ilustra el siguiente ejemplo:

Partes extrañas y partes distintas

Entre las 22 particiones del número 8, hay 6 que contienen solo partes impares :

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Alternativamente, podríamos contar particiones en las que ningún número aparece más de una vez. Este tipo de partición se denomina partición con partes diferenciadas . Si contamos las particiones de 8 con partes diferenciadas, obtenemos también 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

Esta es una propiedad general. Para cada número positivo, el número de particiones con partes impares es igual al número de particiones con partes distintas, denotado por q ( n ). ^{[8] [9]} Este resultado fue demostrado por Leonhard Euler en 1748 ^[10] y luego se generalizó como el teorema de Glaisher .

Para cada tipo de partición restringida existe una función correspondiente para el número de particiones que satisfacen la restricción dada. Un ejemplo importante es q ( n ) (particiones en partes distintas). Los primeros valores de q ( n ) son (comenzando con q (0)=1):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (secuencia A000009 en la OEIS ).

La función generadora para q ( n ) está dada por ^[11]

${\displaystyle \sum _{n=0}^{\infty }q(n)x^{n}=\prod _{k=1}^{\infty }(1+x^{k})=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}.}$

El teorema del número pentagonal da una recurrencia para q : ^[12]

q ( ​​k ) = a _k + q ( k − 1) + q ( k − 2) − q ( k − 5) − q ( k − 7) + q ( k − 12) + q ( k − 15) − q ( k − 22) − ...

donde a _k es (−1) ^m si k = 3 m ² − m para algún entero m y es 0 en caso contrario.

Tamaño de pieza o número de piezas restringido

Tomando conjugados, el número p _k ( n ) de particiones de n en exactamente k partes es igual al número de particiones de n en las que la parte más grande tiene tamaño k . La función p _k ( n ) satisface la recurrencia

pk ( n ) = pk ( n − _k ) + pk _{− 1} ( n − ₁ )

con valores iniciales p ₀ (0) = 1 y p _k ( n ) = 0 si n ≤ 0 o k ≤ 0 y n y k no son ambos cero. ^[13]

Se recupera la función p ( n ) mediante

${\displaystyle p(n)=\sum _{k=0}^{n}p_{k}(n).}$

Una posible función generadora para tales particiones, tomando k fijo y n variable, es

${\displaystyle \sum _{n\geq 0}p_{k}(n)x^{n}=x^{k}\prod _{i=1}^{k}{\frac {1}{1-x^{i}}}.}$

De manera más general, si T es un conjunto de números enteros positivos, entonces el número de particiones de n , todas cuyas partes pertenecen a T , tiene función generadora

${\displaystyle \prod _{t\in T}(1-x^{t})^{-1}.}$

Esto se puede utilizar para resolver problemas de cambio (donde el conjunto T especifica las monedas disponibles). Como dos casos particulares, uno tiene que el número de particiones de n en las que todas las partes son 1 o 2 (o, equivalentemente, el número de particiones de n en 1 o 2 partes) es

${\displaystyle \left\lfloor {\frac {n}{2}}+1\right\rfloor ,}$

y el número de particiones de n en las que todas las partes son 1, 2 o 3 (o, equivalentemente, el número de particiones de n en tres partes como máximo) es el entero más cercano a ( n + 3) ² / 12. ^[14]

Particiones en un rectángulo y coeficientes binomiales gaussianos

También se puede limitar simultáneamente el número y el tamaño de las partes. Sea p ( N , M ; n ) el número de particiones de n con a lo sumo M partes, cada una de tamaño a lo sumo N . Equivalentemente, estas son las particiones cuyo diagrama de Young encaja dentro de un rectángulo M × N . Hay una relación de recurrencia que se obtiene al observar que cuenta las particiones de n en exactamente M partes de tamaño a lo sumo N , y restando 1 de cada parte de dicha partición se obtiene una partición de n − M en a lo sumo M partes. ^[15] $${\displaystyle p(N,M;n)=p(N,M-1;n)+p(N-1,M;n-M)}$$ ${\displaystyle p(N,M;n)-p(N,M-1;n)}$

El coeficiente binomial gaussiano se define como: El coeficiente binomial gaussiano está relacionado con la función generadora de p ( N , M ; n ) por la igualdad $${\displaystyle {k+\ell \choose \ell }_{q}={k+\ell \choose k}_{q}={\frac {\prod _{j=1}^{k+\ell }(1-q^{j})}{\prod _{j=1}^{k}(1-q^{j})\prod _{j=1}^{\ell }(1-q^{j})}}.}$$ $${\displaystyle \sum _{n=0}^{MN}p(N,M;n)q^{n}={M+N \choose M}_{q}.}$$

Plaza Rank y Durfee

El rango de una partición es el número más grande k tal que la partición contiene al menos k partes de tamaño al menos k . Por ejemplo, la partición 4 + 3 + 3 + 2 + 1 + 1 tiene rango 3 porque contiene 3 partes que son ≥ 3, pero no contiene 4 partes que son ≥ 4. En el diagrama de Ferrers o diagrama de Young de una partición de rango r , el cuadrado r × r de las entradas en la esquina superior izquierda se conoce como el cuadrado de Durfee :

El cuadrado de Durfee tiene aplicaciones dentro de la combinatoria en las pruebas de varias identidades de partición. ^[16] También tiene cierto significado práctico en la forma del índice h .

A veces también se denomina rango de partición (o rango de Dyson) a una estadística diferente, a saber, la diferencia para una partición de k partes con la parte más grande . Esta estadística (que no está relacionada con la descrita anteriormente) aparece en el estudio de las congruencias de Ramanujan . ${\displaystyle \lambda _{k}-k}$ ${\displaystyle \lambda _{k}}$

Celosía de Young

Existe un orden parcial natural en las particiones dado por la inclusión de diagramas de Young. Este conjunto parcialmente ordenado se conoce como red de Young . La red se definió originalmente en el contexto de la teoría de la representación , donde se utiliza para describir las representaciones irreducibles de grupos simétricos S _n para todo n , junto con sus propiedades de ramificación, en característica cero. También ha recibido un estudio significativo por sus propiedades puramente combinatorias; en particular, es el ejemplo motivador de un conjunto parcial diferencial .

Particiones aleatorias

Existe una teoría profunda de particiones aleatorias elegidas de acuerdo con la distribución de probabilidad uniforme en el grupo simétrico a través de la correspondencia de Robinson–Schensted . En 1977, Logan y Shepp, así como Vershik y Kerov, demostraron que el diagrama de Young de una partición grande típica se vuelve asintóticamente cercano al gráfico de una cierta función analítica minimizando una cierta funcional. En 1988, Baik, Deift y Johansson extendieron estos resultados para determinar la distribución de la subsecuencia creciente más larga de una permutación aleatoria en términos de la distribución de Tracy–Widom . ^[17] Okounkov relacionó estos resultados con la combinatoria de superficies de Riemann y la teoría de la representación. ^{[18] [19]}

Véase también

• Rango de una partición , una noción diferente de rango
• Manivela de una partición
• Orden de dominancia
• Factorización
• Factorización de números enteros
• Partición de un conjunto
• Estrellas y barras (combinatoria)
• Partición de plano
• Número cortés , definido por particiones en números enteros consecutivos
• Partición multiplicativa
• Doce maneras
• Fórmula de muestreo de Ewens
• La fórmula de Faà di Bruno
• Multipartición
• Las identidades de Newton
• Función de partes más pequeñas
• Una partición de Goldbach es la partición de un número par en primos (ver conjetura de Goldbach )
• Función de partición de Kostant

Notas

1. Andrews 1976, pág. 199.
2. Josuat-Vergès, Matthieu (2010), "Biyecciones entre rellenos que evitan patrones de diagramas de Young", Journal of Combinatorial Theory , Serie A, 117 (8): 1218–1230, arXiv : 0801.4928 , doi :10.1016/j.jcta.2010.03.006, MR  2677686, S2CID  15392503.
3. Andrews 1976, pág. 69.
4. Hardy y Wright 2008, pág. 380.
5. Alder, Henry L. (1969). "Identidades de partición: desde Euler hasta el presente". American Mathematical Monthly . 76 (7): 733–746. doi :10.2307/2317861. JSTOR  2317861.
6. Hardy y Wright 2008, pág. 362.
7. Hardy y Wright 2008, pág. 368.
8. Hardy y Wright 2008, pág. 365.
9. La notación sigue a Abramowitz y Stegun 1964, p. 825
10. Andrews, George E. (1971). Teoría de números . Filadelfia: WB Saunders Company. págs. 149-150.
11. Abramowitz y Stegun 1964, pág. 825, 24.2.2 eq. I(B)
12. Abramowitz y Stegun 1964, pág. 826, 24.2.2 eq. II(A)
13. Richard Stanley, Enumerative Combinatorics , volumen 1, segunda edición. Cambridge University Press, 2012. Capítulo 1, sección 1.7.
14. Hardy, GH (1920). Algunos problemas famosos de la teoría de números. Clarendon Press.
15. Andrews 1976, págs. 33-34.
16. Véase, por ejemplo, Stanley 1999, pág. 58.
17. Romik, Dan (2015). Las sorprendentes matemáticas de las subsecuencias crecientes más largas . Instituto de libros de texto de estadística matemática. Nueva York: Cambridge University Press. ISBN 978-1-107-42882-9.
18. Okounkov, Andrei (2000). "Matrices aleatorias y permutaciones aleatorias". International Mathematics Research Notices . 2000 (20): 1043. doi : 10.1155/S1073792800000532 . S2CID  14308256.
19. Okounkov, A. (1 de abril de 2001). "Cuña infinita y particiones aleatorias". Selecta Mathematica . 7 (1): 57–81. arXiv : math/9907127 . doi :10.1007/PL00001398. ISSN  1420-9020. S2CID  119176413.

Referencias

• Abramowitz, Milton ; Stegun, Irene (1964). Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas . Departamento de Comercio de los Estados Unidos, Oficina Nacional de Normas. ISBN 0-486-61272-4.
• Andrews, George E. (1976). La teoría de particiones . Cambridge University Press. ISBN 0-521-63766-X.
• Andrews, George E.; Eriksson, Kimmo (2004). Particiones enteras . Cambridge University Press. ISBN 0-521-60090-1.
• Apostol, Tom M. (1990) [1976]. Funciones modulares y series de Dirichlet en teoría de números . Textos de posgrado en matemáticas . Vol. 41 (2.ª ed.). Nueva York, etc.: Springer-Verlag . ISBN. 0-387-97127-0.Zbl 0697.10023  . (Véase el capítulo 5 para una introducción pedagógica moderna a la fórmula de Rademacher) .
• Bóna, Miklós (2002). Un recorrido por la combinatoria: una introducción a la enumeración y la teoría de grafos . World Scientific Publishing. ISBN 981-02-4900-4.(una introducción elemental al tema de las particiones enteras, incluyendo un análisis de los gráficos de Ferrers)
• Hardy, GH ; Wright, EM (2008) [1938]. Introducción a la teoría de números . Revisado por DR Heath-Brown y JH Silverman . Prólogo de Andrew Wiles . (6.ª ed.). Oxford: Oxford University Press . ISBN 978-0-19-921986-5. Sr.  2445243. Zbl  1159.11001.
• Lehmer, DH (1939). "Sobre el resto y la convergencia de la serie para la función de partición". Trans. Amer. Math. Soc . 46 : 362–373. doi : 10.1090/S0002-9947-1939-0000410-9 . MR  0000410. Zbl  0022.20401.Proporciona la fórmula principal (sin derivadas), el resto y la forma más antigua para A _k ( n ).)
• Gupta, Hansraj; Gwyther, CE; Miller, JCP (1962). Royal Society of Math. Tablas . Vol. 4, Tablas de particiones. _{(Tiene texto, bibliografía casi completa, pero ellos (y Abramowitz} ) pasaron por alto la fórmula de Selberg para Ak ( n ), que está en Whiteman.)
• Macdonald, Ian G. (1979). Funciones simétricas y polinomios de Hall . Oxford Mathematical Monographs. Oxford University Press . ISBN 0-19-853530-9.Zbl 0487.20007  .(Véase la sección I.1)
• Nathanson, MB (2000). Métodos elementales en teoría de números . Textos de posgrado en matemáticas. Vol. 195. Springer-Verlag . ISBN. 0-387-98912-9.Zbl 0953.11002  .
• Rademacher, Hans (1974). Documentos recopilados de Hans Rademacher . Vol. v II. MIT Press. págs. 100–07, 108–22, 460–75.
• Sautoy, Marcus Du. (2003). La música de los números primos . Nueva York: Perennial-HarperCollins. ISBN 9780066210704.
• Stanley, Richard P. (1999). Combinatoria enumerativa. Vol. 1 y 2. Cambridge University Press. ISBN 0-521-56069-1.
• Whiteman, AL (1956). "Una suma conectada con la serie para la función de partición". Revista del Pacífico de Matemáticas . 6 (1): 159–176. doi : 10.2140/pjm.1956.6.159 . Zbl  0071.04004. (Proporciona la fórmula de Selberg. La forma más antigua es la expansión de Fourier finita de Selberg).

Enlaces externos

• "Partición", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Calculadora de particiones y composición
• Weisstein, Eric W. "Partición". MundoMatemático .
• Wilf, Herbert S. Lectures on Integer Partitions (PDF) , archivado (PDF) del original el 24 de febrero de 2021 , consultado el 28 de febrero de 2021
• Conteo con particiones con tablas de referencia a la Enciclopedia en línea de secuencias de números enteros
• Entrada de particiones enteras en la base de datos FindStat
• Módulo Perl Integer::Partition de CPAN
• Algoritmos rápidos para generar particiones enteras
• Generación de todas las particiones: una comparación de dos codificaciones
• Grime, James (28 de abril de 2016). "Partitions - Numberphile" (video) . Brady Haran . Archivado desde el original el 11 de diciembre de 2021. Consultado el 5 de mayo de 2016 .