En filogenética y filogenética computacional , la parsimonia máxima es un criterio de optimalidad bajo el cual se define el árbol filogenético que minimiza el número total de cambios de estado de carácter (o minimiza el costo de los cambios de estado de carácter ponderados diferencialmente). Bajo el criterio de máxima parsimonia, el árbol óptimo minimizará la cantidad de homoplasia (es decir, evolución convergente , evolución paralela y reversiones evolutivas ). En otras palabras, bajo este criterio, el árbol más corto posible que explique los datos se considera mejor. Algunas de las ideas básicas detrás de la parsimonia máxima fueron presentadas por James S. Farris [1] en 1970 y Walter M. Fitch en 1971. [2]
La máxima parsimonia es un criterio intuitivo y simple, y es popular por esta razón. Sin embargo, aunque es fácil puntuar un árbol filogenético (contando el número de cambios de estado de carácter), no existe un algoritmo para generar rápidamente el árbol más parsimonioso. En cambio, el árbol más parsimonioso debe buscarse en el "espacio de árboles" (es decir, entre todos los árboles posibles). Para un pequeño número de taxones (es decir, menos de nueve) es posible hacer una búsqueda exhaustiva , en la que se puntúan todos los árboles posibles y se selecciona el mejor. Para nueve a veinte taxones, generalmente será preferible usar branch-and-bound , que también garantiza que devolverá el mejor árbol. Para un mayor número de taxones, se debe realizar una búsqueda heurística .
Como el árbol más parsimonioso es siempre el más corto posible, esto significa que, en comparación con un árbol "verdadero" hipotético que realmente describe la historia evolutiva desconocida de los organismos en estudio, el "mejor" árbol según el criterio de máxima parsimonia a menudo subestimará el cambio evolutivo real que podría haber ocurrido. Además, la máxima parsimonia no es estadísticamente consistente. Es decir, no se garantiza que produzca el árbol verdadero con alta probabilidad, dados los datos suficientes. Como lo demostró en 1978 Joe Felsenstein [3] , la máxima parsimonia puede ser inconsistente bajo ciertas condiciones, como la atracción de ramas largas . Por supuesto, cualquier algoritmo filogenético también podría ser estadísticamente inconsistente si el modelo que emplea para estimar el árbol preferido no coincide con precisión con la forma en que ocurrió la evolución en ese clado. Esto es incognoscible. Por lo tanto, si bien la consistencia estadística es una propiedad teórica interesante, queda fuera del ámbito de la comprobabilidad y es irrelevante para los estudios filogenéticos empíricos [4] .
En filogenética, la parsimonia se interpreta principalmente como una preferencia por los árboles que minimizan la cantidad de cambio evolutivo requerido (ver por ejemplo [2] ). Alternativamente, la parsimonia filogenética puede caracterizarse como una preferencia por los árboles que maximizan el poder explicativo al minimizar la cantidad de similitudes observadas que no pueden explicarse por herencia y descendencia común. [5] [6] La minimización del cambio evolutivo requerido por un lado y la maximización de las similitudes observadas que pueden explicarse como homología por el otro pueden dar como resultado diferentes árboles preferidos cuando algunas características observadas no son aplicables en algunos grupos que están incluidos en el árbol, y este último puede verse como el enfoque más general. [7] [8] [9]
Si bien la evolución no es un proceso inherentemente parsimonioso, siglos de experiencia científica respaldan el principio de parsimonia antes mencionado ( la navaja de Occam ). Es decir, la suposición de una cadena de eventos más simple y más parsimoniosa es preferible a la suposición de una cadena de eventos más complicada y menos parsimoniosa. Por lo tanto, la parsimonia ( sensu lato ) se busca típicamente al inferir árboles filogenéticos y, en general, en la explicación científica. [10]
La parsimonia es parte de una clase de métodos de estimación de árboles basados en caracteres que utilizan una matriz de caracteres filogenéticos discretos y estados de caracteres para inferir uno o más árboles filogenéticos óptimos para un conjunto de taxones , comúnmente un conjunto de especies o poblaciones reproductivamente aisladas de una sola especie. Estos métodos operan evaluando árboles filogenéticos candidatos de acuerdo con un criterio de optimalidad explícito ; el árbol con la puntuación más favorable se toma como la mejor hipótesis de las relaciones filogenéticas de los taxones incluidos. La parsimonia máxima se utiliza con la mayoría de los tipos de datos filogenéticos; hasta hace poco, era el único método de estimación de árboles basado en caracteres ampliamente utilizado para datos morfológicos.
Inferir filogenias no es un problema trivial. Existe una enorme cantidad de posibles árboles filogenéticos para cualquier conjunto de taxones de tamaño razonable; por ejemplo, unas diez especies dan lugar a más de dos millones de posibles árboles sin raíz. Se deben buscar estas posibilidades para encontrar un árbol que se ajuste mejor a los datos según el criterio de optimalidad. Sin embargo, los datos en sí mismos no conducen a una solución aritmética simple del problema. Idealmente, esperaríamos que la distribución de cualquier carácter evolutivo (como los rasgos fenotípicos o los alelos ) siguiera directamente el patrón de ramificación de la evolución. Así, podríamos decir que si dos organismos poseen un carácter compartido, deberían estar más estrechamente relacionados entre sí que con un tercer organismo que carece de ese carácter (siempre que ese carácter no estuviera presente en el último ancestro común de los tres, en cuyo caso sería una simplemomorfia ). Podríamos predecir que los murciélagos y los monos están más estrechamente relacionados entre sí que con un elefante, porque los murciélagos y los monos machos poseen testículos externos , de los que carecen los elefantes. Sin embargo, no podemos decir que los murciélagos y los monos estén más estrechamente relacionados entre sí que con las ballenas, aunque los dos tienen testículos externos ausentes en las ballenas, porque creemos que los machos de la última especie ancestral común de los tres tenían testículos externos.
Sin embargo, los fenómenos de evolución convergente , evolución paralela y reversiones evolutivas (denominados colectivamente homoplasia ) añaden un desagradable problema al problema de inferir la filogenia. Por varias razones, dos organismos pueden poseer un rasgo que se infiere que no estuvo presente en su último ancestro común: si tomáramos ingenuamente la presencia de este rasgo como evidencia de una relación, inferiríamos un árbol incorrecto. Los datos filogenéticos empíricos pueden incluir homoplasia sustancial, con diferentes partes de los datos que sugieren a veces relaciones muy diferentes. Los métodos utilizados para estimar árboles filogenéticos tienen la intención explícita de resolver el conflicto dentro de los datos eligiendo el árbol filogenético que se ajuste mejor a todos los datos en general, aceptando que algunos datos simplemente no encajarán. A menudo se cree erróneamente que la parsimonia supone que la convergencia es rara; De hecho, incluso los caracteres derivados de manera convergente tienen cierto valor en los análisis filogenéticos basados en la máxima parsimonia, y la prevalencia de la convergencia no afecta sistemáticamente el resultado de los métodos basados en la parsimonia. [11]
Los datos que no encajan perfectamente en un árbol no son simplemente "ruido", pueden contener señales filogenéticas relevantes en algunas partes de un árbol, incluso si entran en conflicto con el árbol en general. En el ejemplo de la ballena dado anteriormente, la falta de testículos externos en las ballenas es homoplásica: refleja un retorno a la condición que se infiere que estuvo presente en los ancestros antiguos de los mamíferos, cuyos testículos eran internos. Esta similitud inferida entre las ballenas y los ancestros de los mamíferos antiguos está en conflicto con el árbol que aceptamos en función del peso de otros caracteres, ya que implica que los mamíferos con testículos externos deberían formar un grupo que excluya a las ballenas. Sin embargo, entre las ballenas, la inversión a los testículos internos en realidad asocia correctamente los diversos tipos de ballenas (incluidos los delfines y las marsopas) en el grupo Cetacea . Aún así, la determinación del árbol que mejor se ajusta (y, por lo tanto, qué datos no encajan en el árbol) es un proceso complejo. La parsimonia máxima es un método desarrollado para hacer esto.
Los datos de entrada utilizados en un análisis de máxima parsimonia se presentan en forma de "caracteres" para un rango de taxones. No existe una definición generalmente aceptada de un carácter filogenético, pero operacionalmente un carácter puede considerarse como un atributo, un eje a lo largo del cual se observa que varían los taxones. Estos atributos pueden ser físicos (morfológicos), moleculares, genéticos, fisiológicos o conductuales. El único acuerdo generalizado sobre los caracteres parece ser que la variación utilizada para el análisis de caracteres debe reflejar la variación hereditaria . No se ha resuelto por completo si debe ser directamente hereditaria o si la herencia indirecta (por ejemplo, los comportamientos aprendidos) es aceptable.
Cada carácter se divide en estados de carácter discretos , en los que se clasifican las variaciones observadas. Los estados de carácter se formulan a menudo como descriptores, que describen la condición del sustrato del carácter. Por ejemplo, el carácter "color de ojos" podría tener los estados "azul" y "marrón". Los caracteres pueden tener dos o más estados (pueden tener solo uno, pero estos caracteres no aportan nada a un análisis de máxima parsimonia y a menudo se excluyen).
La codificación de caracteres para el análisis filogenético no es una ciencia exacta y existen numerosos problemas que la complican. Normalmente, los taxones se califican con el mismo estado si son más similares entre sí en ese atributo en particular que cada uno con taxones calificados con un estado diferente. Esto no es sencillo cuando los estados de los caracteres no están claramente delineados o cuando no logran capturar toda la variación posible en un carácter. ¿Cómo se calificaría el carácter mencionado anteriormente para un taxón (o individuo) con ojos color avellana? ¿O verdes? Como se señaló anteriormente, la codificación de caracteres generalmente se basa en la similitud: los ojos color avellana y verdes pueden agruparse con el azul porque son más similares a ese color (por ser claros), y el carácter podría entonces recodificarse como "color de ojos: claro; oscuro". Alternativamente, puede haber caracteres de múltiples estados, como "color de ojos: marrón; avellana, azul; verde".
Las ambigüedades en la delimitación y puntuación del estado de los caracteres pueden ser una fuente importante de confusión, disputas y errores en el análisis filogenético que utiliza datos de caracteres. Nótese que, en el ejemplo anterior, "ojos: presente; ausente" también es un carácter posible, lo que crea problemas porque "color de ojos" no es aplicable si los ojos no están presentes. Para tales situaciones, se puntúa un "?" ("desconocido"), aunque a veces se utilizan "X" o "-" (este último generalmente en datos de secuencia ) para distinguir los casos en los que no se puede puntuar un carácter de un caso en el que el estado es simplemente desconocido. Las implementaciones actuales de máxima parsimonia generalmente tratan los valores desconocidos de la misma manera: las razones por las que se desconocen los datos no tienen un efecto particular en el análisis. Efectivamente, el programa trata un ? como si tuviera el estado que implicaría la menor cantidad de pasos adicionales en el árbol (ver más abajo), aunque este no es un paso explícito en el algoritmo.
Los datos genéticos son particularmente susceptibles a los métodos filogenéticos basados en caracteres, como la máxima parsimonia, porque las secuencias de proteínas y nucleótidos son naturalmente discretas: una posición particular en una secuencia de nucleótidos puede ser adenina , citosina , guanina o timina / uracilo , o un espacio en la secuencia; una posición ( residuo ) en una secuencia de proteínas será uno de los aminoácidos básicos o un espacio en la secuencia. Por lo tanto, la puntuación de caracteres rara vez es ambigua, excepto en los casos en que los métodos de secuenciación no producen una asignación definitiva para una posición de secuencia particular. Los espacios en la secuencia a veces se tratan como caracteres, aunque no hay consenso sobre cómo deben codificarse.
Los caracteres pueden ser tratados como desordenados u ordenados. Para un carácter binario (de dos estados), esto hace poca diferencia. Para un carácter de múltiples estados, se puede pensar que los caracteres desordenados tienen un "costo" igual (en términos de número de "eventos evolutivos") para cambiar de un estado a otro; complementariamente, no requieren pasar por estados intermedios. Los caracteres ordenados tienen una secuencia particular en la que los estados deben ocurrir a través de la evolución, de modo que pasar de un estado a otro requiere pasar por un intermedio. Esto se puede pensar complementariamente como tener diferentes costos para pasar de un par de estados a otro. En el ejemplo del color de ojos anterior, es posible dejarlo desordenado, lo que impone el mismo "costo" evolutivo para pasar de marrón-azul, verde-azul, verde-avellana, etc. Alternativamente, podría ser ordenado marrón-avellana-verde-azul; esto normalmente implicaría que costaría dos eventos evolutivos pasar de marrón-verde, tres de marrón-azul, pero solo uno de marrón-avellana. También se puede pensar que esto requiere que los ojos evolucionen a través de una "etapa avellana" para pasar del marrón al verde, y una "etapa verde" para pasar del avellana al azul, etc. Para muchos caracteres, no es obvio si se deben ordenar y cómo. Por el contrario, para los caracteres que representan la discretización de una variable continua subyacente, como los caracteres de forma, tamaño y proporción, el orden es lógico, [12] y las simulaciones han demostrado que esto mejora la capacidad de recuperar clados correctos, al tiempo que disminuye la recuperación de clados erróneos. [13] [14] [15]
Existe un intenso debate sobre la utilidad y la idoneidad de ordenar los caracteres, pero no hay consenso. Algunas autoridades ordenan los caracteres cuando existe una clara transición lógica, ontogenética o evolutiva entre los estados (por ejemplo, "piernas: cortas; medianas; largas"). Algunas aceptan solo algunos de estos criterios. Algunas realizan un análisis no ordenado y ordenan los caracteres que muestran un orden claro de transición en el árbol resultante (práctica que podría ser acusada de razonamiento circular ). Algunas autoridades se niegan a ordenar los caracteres en absoluto, sugiriendo que sesga el análisis exigir que las transiciones evolutivas sigan un camino particular.
También es posible aplicar una ponderación diferencial a caracteres individuales. Esto se hace generalmente en relación con un "costo" de 1. Por lo tanto, algunos caracteres pueden ser vistos como más propensos a reflejar las verdaderas relaciones evolutivas entre taxones, y por lo tanto pueden ser ponderados con un valor de 2 o más; los cambios en estos caracteres entonces contarían como dos "pasos" evolutivos en lugar de uno al calcular las puntuaciones de los árboles (ver más abajo). Ha habido mucha discusión en el pasado sobre la ponderación de caracteres. La mayoría de las autoridades ahora ponderan todos los caracteres por igual, aunque las excepciones son comunes. Por ejemplo, los datos de frecuencia de alelos a veces se agrupan en contenedores y se califican como un carácter ordenado. En estos casos, el carácter en sí mismo a menudo se pondera de manera que los pequeños cambios en las frecuencias de alelos cuentan menos que los cambios importantes en otros caracteres. Además, la tercera posición del codón en una secuencia de nucleótidos codificante es particularmente lábil, y a veces se pondera de manera reducida, o se le da un peso de 0, asumiendo que es más probable que presente homoplasia. En algunos casos, se ejecutan análisis repetidos, con caracteres reponderados en proporción inversa al grado de homoplasia descubierto en el análisis anterior (denominado ponderación sucesiva); esta es otra técnica que podría considerarse razonamiento circular .
Los cambios de estado de los caracteres también se pueden ponderar individualmente. Esto se hace a menudo para los datos de secuencias de nucleótidos ; se ha determinado empíricamente que ciertos cambios de bases (AC, AT, GC, GT y los cambios inversos) ocurren con mucha menos frecuencia que otros (AG, CT y sus cambios inversos). Por lo tanto, estos cambios suelen tener mayor ponderación. Como se muestra arriba en la discusión sobre el ordenamiento de caracteres, los caracteres ordenados se pueden considerar como una forma de ponderación del estado de los caracteres.
Algunos sistemáticos prefieren excluir caracteres que se sabe o se sospecha que son altamente homoplásticos o que tienen una gran cantidad de entradas desconocidas ("?"). Como se indica a continuación, los trabajos teóricos y de simulación han demostrado que es probable que esto sacrifique la precisión en lugar de mejorarla. Esto también sucede con caracteres que son variables en los taxones terminales: los estudios teóricos, de congruencia y de simulación han demostrado que dichos caracteres polimórficos contienen información filogenética significativa. [ cita requerida ]
El tiempo necesario para un análisis de parsimonia (o cualquier análisis filogenético) es proporcional al número de taxones (y caracteres) incluidos en el análisis. Además, como más taxones requieren más ramas para ser estimados, se puede esperar más incertidumbre en análisis grandes. Como los costos de recolección de datos en tiempo y dinero a menudo escalan directamente con el número de taxones incluidos, la mayoría de los análisis incluyen solo una fracción de los taxones que podrían haberse muestreado. De hecho, algunos autores han sostenido que cuatro taxones (el mínimo requerido para producir un árbol sin raíz significativo) son todo lo que se necesita para un análisis filogenético preciso, y que más caracteres son más valiosos que más taxones en filogenética. Esto ha llevado a una gran controversia sobre el muestreo de taxones.
Los estudios empíricos, teóricos y de simulación han llevado a una serie de demostraciones espectaculares de la importancia de un muestreo adecuado de taxones. La mayoría de ellas se pueden resumir con una simple observación: una matriz de datos filogenéticos tiene dimensiones de caracteres multiplicadas por taxones. Duplicar el número de taxones duplica la cantidad de información en una matriz con la misma seguridad que duplicar el número de caracteres. Cada taxón representa una nueva muestra para cada carácter, pero, lo que es más importante, representa (normalmente) una nueva combinación de estados de caracteres. Estos estados de caracteres no sólo pueden determinar dónde se coloca ese taxón en el árbol, sino que pueden informar todo el análisis, posiblemente haciendo que se favorezcan diferentes relaciones entre los taxones restantes al cambiar las estimaciones del patrón de cambios de caracteres.
La debilidad más preocupante del análisis de parsimonia, la de la atracción de ramas largas (véase más adelante), es particularmente pronunciada con un muestreo de taxones deficiente, especialmente en el caso de cuatro taxones. Este es un caso bien conocido en el que el muestreo de caracteres adicional puede no mejorar la calidad de la estimación. A medida que se agregan taxones, a menudo se rompen ramas largas (especialmente en el caso de los fósiles), mejorando efectivamente la estimación de los cambios de estado de los caracteres a lo largo de ellas. Debido a la riqueza de la información agregada por el muestreo de taxones, incluso es posible producir estimaciones altamente precisas de filogenias con cientos de taxones utilizando solo unos pocos miles de caracteres. [ cita requerida ]
Aunque se han realizado muchos estudios, todavía queda mucho por hacer en las estrategias de muestreo de taxones. Debido a los avances en el rendimiento informático y a la reducción de costes y la mayor automatización de la secuenciación molecular, los tamaños de las muestras en general están aumentando y los estudios que abordan las relaciones de cientos de taxones (u otras entidades terminales, como los genes) se están volviendo comunes. Por supuesto, esto no quiere decir que añadir caracteres no sea también útil; el número de caracteres también está aumentando.
Algunos sistemáticos prefieren excluir taxones en función de la cantidad de entradas de caracteres desconocidos ("?") que presentan, o porque tienden a "saltar de un lado a otro" del árbol en los análisis (es decir, son "comodines"). Como se indica a continuación, los trabajos teóricos y de simulación han demostrado que es probable que esto sacrifique la precisión en lugar de mejorarla. Aunque estos taxones pueden generar árboles más parsimoniosos (véase más adelante), métodos como los subárboles de acuerdo y el consenso reducido aún pueden extraer información sobre las relaciones de interés.
Se ha observado que la inclusión de más taxones tiende a reducir los valores de apoyo generales ( porcentajes de bootstrap o índices de decaimiento, ver más abajo). La causa de esto es clara: a medida que se añaden taxones adicionales a un árbol, subdividen las ramas a las que se unen y, por lo tanto, diluyen la información que apoya esa rama. Si bien se reduce el apoyo a las ramas individuales, en realidad aumenta el apoyo a las relaciones generales. Consideremos un análisis que produce el siguiente árbol: (pez, (lagarto, (ballena, (gato, mono)))). Añadir una rata y una morsa probablemente reducirá el apoyo al clado (ballena, (gato, mono)), porque la rata y la morsa pueden caer dentro de este clado, o fuera del clado, y dado que estos cinco animales están todos relativamente relacionados, debería haber más incertidumbre sobre sus relaciones. Dentro del error, puede ser imposible determinar cualquiera de las relaciones de estos animales entre sí. Sin embargo, la rata y la morsa probablemente agregarán datos de carácter que consolidarán la agrupación de dos de estos mamíferos excluyendo al pez o al lagarto; Si bien el análisis inicial podría haber sido engañoso, por ejemplo, por la presencia de aletas en los peces y en la ballena, la presencia de la morsa, con grasa y aletas como las de una ballena pero bigotes como los de un gato y una rata, vincula firmemente a la ballena con los mamíferos.
Para hacer frente a este problema, los subárboles de acuerdo, el consenso reducido y el análisis de doble desintegración buscan identificar relaciones respaldadas (en forma de "enunciados de n taxones", como el enunciado de cuatro taxones "(pez, (lagarto, (gato, ballena)))") en lugar de árboles completos. Si el objetivo de un análisis es un árbol resuelto, como es el caso de la filogenética comparativa , estos métodos no pueden resolver el problema. Sin embargo, si la estimación del árbol está tan poco respaldada, los resultados de cualquier análisis derivado del árbol probablemente serán demasiado sospechosos para usarlos de todos modos.
Un análisis de máxima parsimonia se ejecuta de una manera muy sencilla. Los árboles se califican según el grado en que implican una distribución parsimoniosa de los datos de caracteres. El árbol más parsimonioso para el conjunto de datos representa la hipótesis preferida de relaciones entre los taxones en el análisis.
Los árboles se califican (evalúan) mediante un algoritmo simple que determina cuántos "pasos" (transiciones evolutivas) se requieren para explicar la distribución de cada carácter. Un paso es, en esencia, un cambio de un estado de carácter a otro, aunque con caracteres ordenados algunas transiciones requieren más de un paso. Contrariamente a la creencia popular, el algoritmo no asigna explícitamente estados de caracteres particulares a nodos (uniones de ramas) en un árbol: la menor cantidad de pasos puede implicar múltiples asignaciones y distribuciones igualmente costosas de transiciones evolutivas. Lo que se optimiza es el número total de cambios.
Hay muchos más árboles filogenéticos posibles de los que se pueden buscar exhaustivamente para más de ocho taxones aproximadamente. Por lo tanto, se utilizan varios algoritmos para buscar entre los árboles posibles. Muchos de ellos implican tomar un árbol inicial (normalmente el árbol favorito de la última iteración del algoritmo) y alterarlo para ver si el cambio produce una puntuación más alta.
Los árboles resultantes de la búsqueda de parsimonia no tienen raíz: muestran todas las relaciones posibles de los taxones incluidos, pero carecen de cualquier declaración sobre los tiempos relativos de divergencia. El usuario elige una rama particular para enraizar el árbol. Luego, se considera que esta rama está fuera de todas las demás ramas del árbol, que juntas forman un grupo monofilético . Esto imparte una sensación de tiempo relativo al árbol. La elección incorrecta de una raíz puede dar como resultado relaciones incorrectas en el árbol, incluso si el árbol en sí es correcto en su forma no enraizada.
El análisis de parsimonia suele generar una cantidad de árboles más parsimoniosos (MPT, por sus siglas en inglés). Una gran cantidad de MPT suele considerarse un fallo analítico y se cree que está relacionada con la cantidad de entradas faltantes ("?") en el conjunto de datos, caracteres que muestran demasiada homoplasia o la presencia de taxones "comodín" topológicamente lábiles (que pueden tener muchas entradas faltantes). Se han propuesto numerosos métodos para reducir la cantidad de MPT, incluida la eliminación de caracteres o taxones con grandes cantidades de datos faltantes antes del análisis, la eliminación o reducción de la ponderación de caracteres altamente homoplásticos (ponderación sucesiva) o la eliminación de taxones comodín (método del tronco filogenético) a posteriori y luego el reanálisis de los datos.
Numerosos estudios teóricos y de simulación han demostrado que los caracteres altamente homoplásticos, los caracteres y taxones con abundantes datos faltantes y los taxones "comodín" contribuyen al análisis. Aunque excluir caracteres o taxones puede parecer que mejora la resolución, el árbol resultante se basa en menos datos y, por lo tanto, es una estimación menos confiable de la filogenia (a menos que los caracteres o taxones no sean informativos, consulte reducción taxonómica segura). El consenso general actual es que tener múltiples MPT es un resultado analítico válido; simplemente indica que no hay datos suficientes para resolver el árbol por completo. En muchos casos, existe una estructura común sustancial en los MPT y las diferencias son leves e implican incertidumbre en la ubicación de algunos taxones. Hay varios métodos para resumir las relaciones dentro de este conjunto, incluidos los árboles de consenso, que muestran relaciones comunes entre todos los taxones, y los subárboles de acuerdo podados, que muestran una estructura común podando temporalmente los taxones "comodín" de cada árbol hasta que todos concuerden. El consenso reducido lleva esto un paso más allá al mostrar todos los subárboles (y, por lo tanto, todas las relaciones) soportadas por los árboles de entrada.
Incluso si se obtienen múltiples MPT, el análisis de parsimonia sigue produciendo básicamente una estimación puntual, sin intervalos de confianza de ningún tipo. Esto se ha criticado a menudo, ya que sin duda hay un error en la estimación del árbol más parsimonioso, y el método no incluye inherentemente ningún medio para establecer la sensibilidad de sus conclusiones a este error. Se han utilizado varios métodos para evaluar el respaldo.
El método jackknifing y el bootstrapping , procedimientos estadísticos de remuestreo bien conocidos , se han empleado con el análisis de parsimonia. El método jackknife, que implica un remuestreo sin reemplazo ("dejar uno afuera"), se puede emplear en caracteres o taxones; la interpretación puede volverse complicada en el último caso, porque la variable de interés es el árbol, y la comparación de árboles con diferentes taxones no es sencilla. El método bootstrap, remuestreo con reemplazo (muestrear x elementos al azar de una muestra de tamaño x, pero los elementos pueden seleccionarse varias veces), solo se utiliza en caracteres, porque agregar taxones duplicados no cambia el resultado de un análisis de parsimonia. El método bootstrap se emplea mucho más comúnmente en filogenética (como en otras áreas); ambos métodos implican un número arbitrario pero grande de iteraciones repetidas que implican la perturbación de los datos originales seguida de un análisis. Los MPT resultantes de cada análisis se agrupan y los resultados suelen presentarse en un árbol de consenso de regla de mayoría del 50%, con ramas individuales (o nodos) etiquetados con el porcentaje de MPT de bootstrap en el que aparecen. Este "porcentaje de bootstrap" (que no es un valor P , como a veces se afirma) se utiliza como una medida de apoyo. Técnicamente, se supone que es una medida de repetibilidad, la probabilidad de que esa rama (nodo, clado) se recuperaría si se muestrearan nuevamente los taxones. Las pruebas experimentales con filogenias virales sugieren que el porcentaje de bootstrap no es un buen estimador de repetibilidad para la filogenia, pero es un estimador razonable de precisión. [ cita requerida ] De hecho, se ha demostrado que el porcentaje de bootstrap, como estimador de precisión, está sesgado, y que este sesgo resulta en promedio en una subestimación de la confianza (de modo que tan solo un 70% de apoyo podría indicar realmente hasta un 95% de confianza). Sin embargo, la dirección del sesgo no se puede determinar en casos individuales, por lo que suponer que valores altos de soporte bootstrap indican una confianza aún mayor no está justificado.
Otro medio para evaluar el soporte es el soporte de Bremer, [16] [17] o el índice de decaimiento que es un parámetro de un conjunto de datos dado, en lugar de una estimación basada en submuestras pseudorreplicadas, como lo son los procedimientos bootstrap y jackknife descritos anteriormente. El soporte de Bremer (también conocido como soporte de rama) es simplemente la diferencia en el número de pasos entre la puntuación del MPT(s), y la puntuación del árbol más parsimonioso que no contiene un clado en particular (nodo, rama). Puede considerarse como la cantidad de pasos que debe agregar para perder ese clado; implícitamente, pretende sugerir qué tan grande debe ser el error en la estimación de la puntuación del MPT para que el clado ya no esté respaldado por el análisis, aunque esto no es necesariamente lo que hace. Los valores de soporte de rama suelen ser bastante bajos para conjuntos de datos de tamaño modesto (uno o dos pasos son típicos), pero a menudo parecen ser proporcionales a los porcentajes de bootstrap. A medida que las matrices de datos se vuelven más grandes, los valores de soporte de rama a menudo continúan aumentando a medida que los valores de bootstrap se estabilizan en el 100%. Por lo tanto, para matrices de datos grandes, los valores de soporte de las ramas pueden proporcionar un medio más informativo para comparar el soporte de las ramas fuertemente soportadas. [18] Sin embargo, la interpretación de los valores de decaimiento no es sencilla, y parecen ser los preferidos por los autores con objeciones filosóficas al bootstrap (aunque muchos sistemáticos morfológicos, especialmente paleontólogos, informan ambos). El análisis de doble decaimiento es una contraparte del decaimiento del consenso reducido que evalúa el índice de decaimiento para todas las posibles relaciones de subárboles (declaraciones de n-taxones) dentro de un árbol.
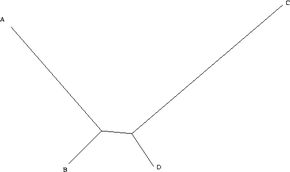
La máxima parsimonia es un enfoque epistemológicamente sencillo que hace pocas suposiciones mecanicistas, y es popular por esta razón. Sin embargo, puede no ser estadísticamente consistente bajo ciertas circunstancias. La consistencia, que aquí significa la convergencia monótona en la respuesta correcta con la adición de más datos, es una propiedad deseable de los métodos estadísticos . Como lo demostró en 1978 Joe Felsenstein , [3] la máxima parsimonia puede ser inconsistente bajo ciertas condiciones. La categoría de situaciones en las que se sabe que esto ocurre se llama atracción de ramas largas , y ocurre, por ejemplo, cuando hay ramas largas (un alto nivel de sustituciones) para dos caracteres (A y C), pero ramas cortas para otros dos (B y D). A y B divergieron de un ancestro común, al igual que C y D. Por supuesto, para saber que un método le está dando la respuesta incorrecta, necesitaría saber cuál es la respuesta correcta. Este generalmente no es el caso en la ciencia. Por esta razón, algunos ven la consistencia estadística como irrelevante para las preguntas filogenéticas empíricas. [19]
Supongamos, para simplificar, que estamos considerando un único carácter binario (puede ser + o -). Como la distancia de B a D es pequeña, en la gran mayoría de los casos, B y D serán iguales. Aquí, supondremos que ambos son + (+ y - se asignan arbitrariamente e intercambiarlos es solo una cuestión de definición). Si este es el caso, quedan cuatro posibilidades. A y C pueden ser ambos +, en cuyo caso todos los taxones son iguales y todos los árboles tienen la misma longitud. A puede ser + y C puede ser -, en cuyo caso solo un carácter es diferente y no podemos aprender nada, ya que todos los árboles tienen la misma longitud. De manera similar, A puede ser - y C puede ser +. La única posibilidad restante es que A y C sean ambos -. En este caso, sin embargo, la evidencia sugiere que A y C se agrupan juntos, y B y D juntos. Como consecuencia, si el "árbol verdadero" es un árbol de este tipo, cuantos más datos recopilemos (es decir, cuantos más caracteres estudiemos), más evidencia respaldará el árbol equivocado. Por supuesto, salvo en las simulaciones matemáticas, nunca sabemos cuál es el "árbol verdadero". Por lo tanto, a menos que seamos capaces de idear un modelo que garantice la recuperación precisa del "árbol verdadero", cualquier otro criterio de optimalidad o esquema de ponderación también podría, en principio, ser estadísticamente inconsistente. La conclusión es que, si bien la inconsistencia estadística es una cuestión teórica interesante, empíricamente es una preocupación puramente metafísica, fuera del ámbito de la comprobación empírica. Cualquier método podría ser inconsistente, y no hay forma de saber con certeza si lo es o no. Es por esta razón que muchos sistemáticos caracterizan sus resultados filogenéticos como hipótesis de relación.
Otra complicación con la máxima parsimonia y otros métodos filogenéticos basados en criterios de optimalidad es que encontrar el árbol más corto es un problema NP-hard . [20] La única forma eficiente disponible actualmente de obtener una solución, dado un conjunto arbitrariamente grande de taxones, es mediante el uso de métodos heurísticos que no garantizan que se recuperará el árbol más corto. Estos métodos emplean algoritmos de escalada de colinas para acercarse progresivamente al mejor árbol. Sin embargo, se ha demostrado que puede haber "islas de árboles" de soluciones subóptimas, y el análisis puede quedar atrapado en estos óptimos locales . Por lo tanto, se requieren heurísticas complejas y flexibles para garantizar que el espacio del árbol se haya explorado adecuadamente. Hay varias heurísticas disponibles, incluido el intercambio del vecino más cercano (NNI), la reconexión de la bisección del árbol (TBR) y el trinquete de parsimonia.
Se ha afirmado que un problema importante, especialmente para la paleontología , es que la parsimonia máxima supone que la única forma en que dos especies pueden compartir el mismo nucleótido en la misma posición es si están relacionadas genéticamente. [ cita requerida ] Esto afirma que las aplicaciones filogenéticas de la parsimonia suponen que toda similitud es homóloga (otras interpretaciones, como la afirmación de que dos organismos podrían no estar relacionados en absoluto, no tienen sentido). Este no es enfáticamente el caso: como con cualquier forma de estimación de filogenia basada en caracteres, la parsimonia se utiliza para probar la naturaleza homóloga de las similitudes al encontrar el árbol filogenético que mejor explica todas las similitudes.
A menudo se afirma que la parsimonia no es relevante para la inferencia filogenética porque "la evolución no es parsimoniosa". [ cita requerida ] En la mayoría de los casos, no se propone una alternativa explícita; si no hay alternativa disponible, cualquier método estadístico es preferible a ninguno. Además, no está claro qué se querría decir si la afirmación "la evolución es parsimoniosa" fuera de hecho cierta. Esto podría interpretarse como que pueden haberse producido más cambios de caracteres históricamente de los que se predicen utilizando el criterio de parsimonia. Dado que la estimación de la filogenia por parsimonia reconstruye el número mínimo de cambios necesarios para explicar un árbol, esto es bastante posible. Sin embargo, se ha demostrado a través de estudios de simulación, pruebas con filogenias virales in vitro conocidas y congruencia con otros métodos, que la precisión de la parsimonia en la mayoría de los casos no se ve comprometida por esto. El análisis de parsimonia utiliza el número de cambios de caracteres en los árboles para elegir el mejor árbol, pero no requiere que exactamente esa cantidad de cambios, y no más, produzca el árbol. Mientras los cambios que no se han tenido en cuenta se distribuyan aleatoriamente en el árbol (una expectativa nula razonable), el resultado no debería estar sesgado. En la práctica, la técnica es robusta: la máxima parsimonia muestra un sesgo mínimo como resultado de elegir el árbol con la menor cantidad de cambios.
Se puede establecer una analogía con la elección entre contratistas en función de su estimación inicial (no vinculante) del coste de un trabajo. Es muy probable que el coste final real sea superior a la estimación. A pesar de ello, elegir al contratista que haya proporcionado la estimación más baja debería dar como resultado teóricamente el coste final del proyecto más bajo. Esto se debe a que, en ausencia de otros datos, supondríamos que todos los contratistas pertinentes tienen el mismo riesgo de sobrecostes. En la práctica, por supuesto, las prácticas comerciales inescrupulosas pueden sesgar este resultado; también en filogenética, algunos problemas filogenéticos particulares (por ejemplo, la atracción de ramas largas , descrita anteriormente) pueden sesgar potencialmente los resultados. En ambos casos, sin embargo, no hay forma de saber si el resultado va a estar sesgado, o en qué grado lo estará, basándose en la estimación misma. Con la parsimonia también, no hay forma de saber que los datos son positivamente engañosos, sin compararlos con otras pruebas.
La parsimonia se caracteriza a menudo como la adopción implícita de la posición de que el cambio evolutivo es raro, o que la homoplasia (convergencia e inversión) es mínima en la evolución. Esto no es del todo cierto: la parsimonia minimiza el número de convergencias e inversiones que se suponen en el árbol preferido, pero esto puede dar lugar a un número relativamente grande de tales eventos homoplásticos. Sería más apropiado decir que la parsimonia supone sólo la cantidad mínima de cambio implícita en los datos. Como antes, esto no requiere que estos fueran los únicos cambios que ocurrieron; simplemente no infiere cambios para los que no hay evidencia. La forma abreviada de describir esto, parafraseando a Farris [5] es que "la parsimonia minimiza las homoplasias supuestas, no supone que la homoplasia sea mínima".
Estudios de simulación recientes sugieren que la parsimonia puede ser menos precisa que los árboles construidos utilizando enfoques bayesianos para datos morfológicos, [21] posiblemente debido a la sobreprecisión, [22] aunque esto ha sido discutido. [23] Estudios que utilizan nuevos métodos de simulación han demostrado que las diferencias entre los métodos de inferencia resultan de la estrategia de búsqueda y el método de consenso empleados, en lugar de la optimización utilizada. [24] Además, los análisis de 38 conjuntos de datos empíricos moleculares y 86 morfológicos han demostrado que el mecanismo común asumido por los modelos evolutivos utilizados en la filogenética basada en modelos se aplica a la mayoría de los conjuntos de datos moleculares, pero a pocos morfológicos. [25] Este hallazgo valida el uso de la filogenética basada en modelos para datos moleculares, pero sugiere que para los datos morfológicos, la parsimonia sigue siendo ventajosa, al menos hasta que haya modelos más sofisticados disponibles para datos fenotípicos.
Existen otros métodos para inferir filogenias basadas en datos de caracteres discretos, incluyendo la máxima verosimilitud y la inferencia bayesiana . Cada uno ofrece ventajas y desventajas potenciales. En la práctica, estos métodos tienden a favorecer árboles que son muy similares a los árboles más parsimoniosos para el mismo conjunto de datos; [26] sin embargo, permiten un modelado complejo de procesos evolutivos, y como clases de métodos son estadísticamente consistentes y no son susceptibles a la atracción de ramas largas . Nótese, sin embargo, que el desempeño de los métodos de verosimilitud y bayesianos dependen de la calidad del modelo particular de evolución empleado; un modelo incorrecto puede producir un resultado sesgado - al igual que la parsimonia. Además, siguen siendo bastante lentos computacionalmente en relación con los métodos de parsimonia, a veces requiriendo semanas para ejecutar grandes conjuntos de datos. La mayoría de estos métodos tienen defensores y detractores particularmente ávidos; la parsimonia especialmente ha sido defendida como filosóficamente superior (más notablemente por ardientes cladistas ). [ cita requerida ] Un área en la que la parsimonia todavía tiene mucha influencia es en el análisis de datos morfológicos, porque, hasta hace poco, no había modelos estocásticos de cambio de caracteres disponibles para datos no moleculares y todavía no se han implementado ampliamente. También se ha demostrado recientemente que la parsimonia tiene más probabilidades de recuperar el árbol verdadero ante cambios profundos en los parámetros evolutivos ("modelo") (por ejemplo, la tasa de cambio evolutivo) dentro de un árbol. [27]
Las matrices de distancia también se pueden utilizar para generar árboles filogenéticos. Los métodos de distancia no paramétricos se aplicaron originalmente a los datos fenéticos utilizando una matriz de distancias por pares y reconciliadas para producir un árbol . La matriz de distancia puede provenir de varias fuentes diferentes, incluidas la distancia inmunológica, el análisis morfométrico y las distancias genéticas . Para los datos de caracteres filogenéticos, los valores de distancia sin procesar se pueden calcular simplemente contando el número de diferencias por pares en los estados de los caracteres ( distancia de Manhattan ) o aplicando un modelo de evolución. En particular, los métodos de distancia también permiten el uso de datos que pueden no convertirse fácilmente en datos de caracteres, como los ensayos de hibridación ADN-ADN . Hoy en día, los métodos basados en la distancia a menudo están mal vistos porque los datos filogenéticamente informativos se pueden perder al convertir caracteres en distancias. Hay varios métodos de matriz de distancia y criterios de optimalidad, de los cuales el criterio de evolución mínima es el más estrechamente relacionado con la parsimonia máxima.
Entre los métodos de distancia , existe un criterio de estimación filogenética, conocido como Evolución Mínima (EM), que comparte con la máxima parsimonia el aspecto de buscar la filogenia que tenga la suma total más corta de longitudes de ramas. [28] [29]
Una sutil diferencia distingue el criterio de máxima parsimonia del criterio ME: mientras que la máxima parsimonia se basa en una heurística abductiva, es decir, la plausibilidad de la hipótesis evolutiva más simple de los taxones con respecto a las más complejas, el criterio ME se basa en las conjeturas de Kidd y Sgaramella-Zonta (probadas 22 años después por Rzhetsky y Nei [30] ) que afirman que si las distancias evolutivas de los taxones fueran estimaciones imparciales de las distancias evolutivas verdaderas, entonces la verdadera filogenia de los taxones tendría una longitud más corta que cualquier otra filogenia alternativa compatible con esas distancias. Los resultados de Rzhetsky y Nei liberan al criterio ME del principio de la navaja de Occam y le confieren una sólida base teórica y cuantitativa. [31]