Distribución parametrizada por cuantiles

Una distribución parametrizada por cuantiles (QPD) es una distribución de probabilidad que está parametrizada directamente por los datos. Fueron creados para satisfacer la necesidad de distribuciones de probabilidad continuas fáciles de usar, lo suficientemente flexibles como para representar una amplia gama de incertidumbres, como las que se encuentran comúnmente en los negocios, la economía, la ingeniería y la ciencia. Debido a que los QPD están parametrizados directamente por los datos, tienen la ventaja práctica de evitar el paso intermedio de la estimación de parámetros , un proceso que requiere mucho tiempo y que generalmente requiere métodos iterativos no lineales para estimar los parámetros de distribución de probabilidad a partir de los datos. Algunos QPD tienen una flexibilidad de forma prácticamente ilimitada y también momentos de forma cerrada.

Historia

El desarrollo de distribuciones parametrizadas por cuantiles se inspiró en la necesidad práctica de distribuciones de probabilidad continuas flexibles que sean fáciles de ajustar a los datos. Históricamente, las familias de distribuciones de Pearson ^[1] y Johnson ^{[2] [3]} se han utilizado cuando se necesita flexibilidad de forma. Esto se debe a que ambas familias pueden hacer coincidir los primeros cuatro momentos (media, varianza, asimetría y curtosis) de cualquier conjunto de datos. Sin embargo, en muchos casos, estas distribuciones son difíciles de ajustar a los datos o no son lo suficientemente flexibles para ajustarlos adecuadamente.

Por ejemplo, la distribución beta es una distribución flexible de Pearson que se utiliza con frecuencia para modelar porcentajes de una población. Sin embargo, si las características de esta población son tales que la función de distribución acumulativa (CDF) deseada debe pasar por ciertos puntos específicos de la CDF, es posible que no exista una distribución beta que satisfaga esta necesidad. Debido a que la distribución beta tiene solo dos parámetros de forma, en general no puede coincidir ni siquiera con tres puntos CDF específicos. Además, los parámetros beta que mejor se ajustan a dichos datos sólo pueden encontrarse mediante métodos iterativos no lineales.

Los profesionales del análisis de decisiones , que necesitaban distribuciones fácilmente parametrizadas por tres o más puntos CDF (por ejemplo, porque dichos puntos se especificaron como resultado de un proceso de obtención de expertos ), inventaron originalmente distribuciones parametrizadas por cuantiles para este propósito. Keelin y Powley (2011) ^[4] proporcionaron la definición original. Posteriormente, Keelin (2016) ^[5] desarrolló las distribuciones metalog , una familia de distribuciones parametrizadas por cuantiles que tiene una flexibilidad de forma prácticamente ilimitada, ecuaciones simples y momentos de forma cerrada.

Definición

Keelin y Powley ^[4] definen una distribución parametrizada por cuantiles como aquella cuya función cuantil (FDC inversa) se puede escribir en la forma

${\displaystyle F^{-1}(y)=\left\{{\begin{array}{cl}L_{0}&{\text{for }}y=0\\\sum _{i=1}^{n}a_{i}g_{i}(y)&{\text{for }}0<y<1\\L_{1}&{\mbox{for }}y=1\end{array}}\right.}$

dónde

${\displaystyle {\begin{array}{rcl}L_{0}&=&\lim _{y\rightarrow 0^{+}}F^{-1}(y)\\L_{1}&=&\lim _{y\rightarrow 1^{-}}F^{-1}(y)\end{array}}}$

y las funciones son funciones de base continuamente diferenciables y linealmente independientes. Aquí, esencialmente, y están los límites inferior y superior (si existen) de una variable aleatoria con función cuantil . Estas distribuciones se denominan parametrizadas por cuantiles porque para un conjunto dado de pares de cuantiles , donde y un conjunto de funciones básicas , los coeficientes se pueden determinar resolviendo un conjunto de ecuaciones lineales. ^[4] Si se desea utilizar más pares de cuantiles que funciones básicas, entonces los coeficientes se pueden elegir para minimizar la suma de errores cuadrados entre los cuantiles indicados y . Keelin y Powley ^[4] ilustran este concepto para una elección específica de funciones básicas que es una generalización de la función cuantil de la distribución normal , para la cual la media y la desviación estándar son funciones lineales de probabilidad acumulativa : ${\displaystyle g_{i}(y)}$ ${\displaystyle L_{0}}$ ${\displaystyle L_{1}}$ ${\displaystyle F^{-1}(y)}$ ${\displaystyle \{(x_{i},y_{i})\mid i=1,\ldots ,n\}}$ ${\displaystyle x_{i}=F^{-1}(y_{i})}$ ${\displaystyle n}$ ${\displaystyle g_{i}(y)}$ ${\displaystyle a_{i}}$ ${\displaystyle a_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle F^{-1}(y_{i})}$ ${\displaystyle x=\mu +\sigma \Phi ^{-1}(y)}$ ${\displaystyle \mu }$ ${\displaystyle \sigma }$ ${\displaystyle y}$

${\displaystyle \mu (y)=a_{1}+a_{4}y}$

${\displaystyle \sigma (y)=a_{2}+a_{3}y}$

El resultado es una distribución de cuatro parámetros que se puede ajustar exactamente a un conjunto de cuatro pares de cuantiles/probabilidad, o a cualquier número de dichos pares mediante mínimos cuadrados lineales . Keelin y Powley ^[4] llaman a esto distribución Q-Normal simple. En las siguientes figuras se muestran algunas PDF Q-Normal simples sesgadas y simétricas.

PDF simétricos simples Q-Normal

PDF Q-Normal simples y sesgados

Propiedades

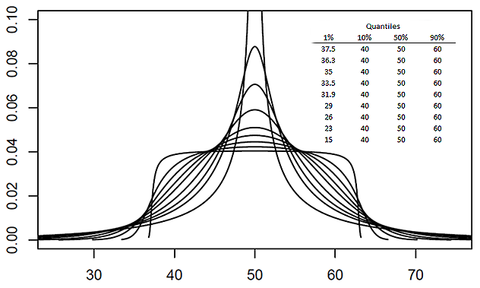
Los QPD que cumplen con la definición de Keelin y Powley tienen las siguientes propiedades.

Función de densidad de probabilidad

Diferenciando respecto a los rendimientos . El recíproco de esta cantidad, es la función de densidad de probabilidad (PDF) ${\displaystyle x=F^{-1}(y)=\sum _{i=1}^{n}a_{i}g_{i}(y)}$ ${\displaystyle y}$ ${\displaystyle dx/dy}$ ${\displaystyle dy/dx}$

${\displaystyle f(y)=\left(\sum _{i=1}^{n}a_{i}{{dg_{i}(y)} \over {dy}}\right)^{-1}}$

dónde . Tenga en cuenta que esta PDF se expresa como una función de probabilidad acumulada en lugar de . Para trazarlo, como se muestra en las figuras, varía paramétricamente. Trazar en el eje horizontal y en el eje vertical. ${\displaystyle 0<y<1}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y\in (0,1)}$ ${\displaystyle x=F^{-1}(y)}$ ${\displaystyle f(y)}$

Factibilidad

Una función de la forma de es una distribución de probabilidad factible si y sólo si para todos . ^[4] Esto implica una restricción de viabilidad sobre el conjunto de coeficientes : ${\displaystyle F^{-1}(y)}$ ${\displaystyle f(y)>0}$ ${\displaystyle y\in (0,1)}$ ${\displaystyle {\boldsymbol {a}}=(a_{1},\ldots ,a_{n})\in \mathbb {R} ^{n}}$

${\displaystyle \sum _{i=1}^{n}a_{i}{{dg_{i}(y)} \over {dy}}>0}$para todos ${\displaystyle y\in (0,1)}$

En aplicaciones prácticas, la viabilidad generalmente debe comprobarse en lugar de asumirse.

Convexidad

El conjunto de coeficientes factibles de una QPD para todos es convexo . Debido a que la optimización convexa requiere conjuntos convexos factibles, esta propiedad simplifica las aplicaciones de optimización que involucran QPD. ${\displaystyle S_{\boldsymbol {a}}=\{{\boldsymbol {a}}\in \mathbb {R} ^{n}\mid \sum _{i=1}^{n}a_{i}dg_{i}(y)/dy>0}$ ${\displaystyle y\in (0,1)\}}$

Ajuste a los datos

Los coeficientes se pueden determinar a partir de datos mediante mínimos cuadrados lineales . Dados los puntos de datos que pretenden caracterizar la CDF de un QPD y la matriz cuyos elementos constan de , entonces, siempre que sea invertible, el vector de columna de los coeficientes se puede determinar como , donde y el vector de columna . Si , esta ecuación se reduce a , donde el CDF resultante recorre todos los puntos de datos exactamente. Un método alternativo, implementado como un programa lineal, determina los coeficientes minimizando la suma de distancias absolutas entre la CDF y los datos sujetos a restricciones de viabilidad. ^[6] ${\displaystyle {\boldsymbol {a}}}$ ${\displaystyle m}$ ${\displaystyle (x_{i},y_{i})}$ ${\displaystyle m\times n}$ ${\displaystyle {\boldsymbol {Y}}}$ ${\displaystyle g_{j}(y_{i})}$ ${\displaystyle {\boldsymbol {Y}}^{T}{\boldsymbol {Y}}}$ ${\displaystyle {\boldsymbol {a}}}$ ${\displaystyle {\boldsymbol {a}}=({\boldsymbol {Y}}^{T}{\boldsymbol {Y}})^{-1}{\boldsymbol {Y}}^{T}{\boldsymbol {x}}}$ ${\displaystyle m\geq n}$ ${\displaystyle {\boldsymbol {x}}=(x_{1},\ldots ,x_{m})}$ ${\displaystyle m=n}$ ${\displaystyle {\boldsymbol {a}}={\boldsymbol {Y}}^{-1}{\boldsymbol {x}}}$

Flexibilidad de forma

Un QPD con términos, donde , tiene parámetros de forma. Por tanto, las QPD pueden ser mucho más flexibles que las distribuciones de Pearson , que tienen como máximo dos parámetros de forma. Por ejemplo, se ha demostrado que las distribuciones metalog de diez términos parametrizadas por 105 puntos CDF de 30 distribuciones de fuentes tradicionales (incluidas normal, t de Student, lognormal, gamma, beta y valor extremo) se aproximan a cada una de estas distribuciones de fuentes dentro de una distribución K-S. distancia de 0,001 o menos. ^[7] ${\displaystyle n}$ ${\displaystyle n\geq 2}$ ${\displaystyle n-2}$

Transformaciones

Las transformaciones QPD se rigen por una propiedad general de las funciones cuantiles: para cualquier función cuantil y una función creciente es una función cuantil . ^[8] Por ejemplo, la función cuantil de la distribución normal , es una QPD según la definición de Keelin y Powley. El logaritmo natural, es una función creciente, al igual que la función cuantil de la distribución lognormal con límite inferior . Es importante destacar que esta transformación convierte una QPD ilimitada en una QPD semilimitada. De manera similar, al aplicar esta transformación logarítmica a la distribución metalog ilimitada ^[9] se obtiene la distribución metalog semilimitada (log) ; ^[10] asimismo, aplicando la transformación logit, se obtiene la distribución metalog acotada (logit) ^[10] con límites inferior y superior y , respectivamente. Además, al considerar distribuida dónde está cualquier QPD que cumpla con la definición de Keelin y Powley, la variable transformada mantiene las propiedades anteriores de viabilidad, convexidad y ajuste a los datos. Estos QPD transformados tienen mayor flexibilidad de forma que los subyacentes , que tienen parámetros de forma; la transformación logarítmica tiene parámetros de forma y la transformación logit tiene parámetros de forma. Además, dichas QPD transformadas comparten el mismo conjunto de coeficientes factibles que las QPD subyacentes no transformadas. ^[11] ${\displaystyle x=Q(y)}$ ${\displaystyle t(x),x=t^{-1}(Q(y))}$ ${\displaystyle x=\mu +\sigma \Phi ^{-1}(y)}$ ${\displaystyle t(x)=\ln(x-b_{l})}$ ${\displaystyle x=b_{l}+e^{\mu +\sigma \Phi ^{-1}(y)}}$ ${\displaystyle b_{l}}$ ${\displaystyle t(x)=\ln((x-b_{l})/(b_{u}-x))}$ ${\displaystyle b_{l}}$ ${\displaystyle b_{u}}$ ${\displaystyle t(x)}$ ${\displaystyle F^{-1}(y)}$ ${\displaystyle F^{-1}(y)}$ ${\displaystyle F^{-1}(y)}$ ${\displaystyle n-2}$ ${\displaystyle n-1}$ ${\displaystyle n}$

Momentos

El momento de un QPD es: ^[4] ${\displaystyle k^{th}}$

${\displaystyle E[x^{k}]=\int _{0}^{1}\left(\sum _{i=1}^{n}a_{i}g_{i}(y)\right)^{k}dy}$

Que tales momentos existan en forma cerrada depende de la elección de las funciones básicas de QPD . La distribución metalog ilimitada y las QPD polinómicas son ejemplos de QPD para las cuales los momentos existen en forma cerrada como funciones de los coeficientes . ${\displaystyle g_{i}(y)}$ ${\displaystyle a_{i}}$

Simulación

Dado que la función cuantil se expresa en forma cerrada, las QPD de Keelin y Powley facilitan la simulación de Monte Carlo . La sustitución de muestras aleatorias distribuidas uniformemente produce muestras aleatorias de en forma cerrada, eliminando así la necesidad de invertir una CDF expresada como . ${\displaystyle x=F^{-1}(y)}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y=F(x)}$

Distribuciones relacionadas

Las siguientes distribuciones de probabilidad son QPD según la definición de Keelin y Powley:

• La función cuantil de la distribución normal . ${\displaystyle x=\mu +\sigma \Phi ^{-1}(y)}$
• La función cuantil de la distribución de Gumbel . ${\displaystyle x=\mu -\beta \ln(-\ln(y))}$
• La función cuantil de la distribución de Cauchy . ${\displaystyle x=x_{0}+\gamma \tan[\pi (y-0.5)]}$
• La función cuantil de la distribución logística . ${\displaystyle x=\mu +s\ln(y/(1-y))}$
• La distribución metalog ilimitada , que es una expansión en serie de potencias de los parámetros y de la función cuantil logística. ${\displaystyle \mu }$ ${\displaystyle s}$
• Las distribuciones metalog semi-acotadas y acotadas , que son las transformadas log y logit, respectivamente, de la distribución metalog ilimitada.
• Las distribuciones de metalogramas ilimitadas, semilimitadas y acotadas SPT (triplete percentil simétrico) , que están parametrizadas por tres puntos CDF y límites superior e inferior opcionales.
• La distribución Q-Normal simple ^[12]
• Las metadistribuciones, incluida la metanormal ^[13]
• Funciones cuantiles expresadas como funciones polinómicas de probabilidad acumulativa , incluidas las funciones polinómicas de Chebyshev . ${\displaystyle y}$

Al igual que las distribuciones metalog de SPT, las distribuciones parametrizadas por cuantiles de Johnson ^{[14] [15]} (JQPD) están parametrizadas por tres cuantiles. Los JQPD no cumplen con la definición de QPD de Keelin y Powley, sino que tienen sus propias propiedades. Los JQPD son factibles para todos los conjuntos de parámetros SPT que sean consistentes con las reglas de probabilidad .

Aplicaciones

Las aplicaciones originales de las QPD fueron realizadas por analistas de decisiones que deseaban convertir convenientemente los cuantiles evaluados por expertos (por ejemplo, cuantiles 10, 50 y 90) en distribuciones de probabilidad continuas y uniformes. Los QPD también se han utilizado para ajustar datos de salida de simulaciones con el fin de representar esos resultados (tanto CDF como PDF) como distribuciones continuas de forma cerrada. ^[16] Utilizados de esta manera, suelen ser más estables y suaves que los histogramas. De manera similar, dado que las QPD pueden imponer menos restricciones de forma que las distribuciones tradicionales, se han utilizado para ajustar una amplia gama de datos empíricos con el fin de representar esos conjuntos de datos como distribuciones continuas (por ejemplo, reflejando la bimodalidad que puede existir en los datos de una manera sencilla). ^[17] ). La parametrización cuantil permite una representación QPD de forma cerrada de distribuciones conocidas cuyas CDF no tienen expresión de forma cerrada. Keelin et al. (2019) ^[18] aplican esto a la suma de distribuciones lognormales independientes distribuidas idénticamente, donde los cuantiles de la suma pueden determinarse mediante una gran cantidad de simulaciones. Nueve de estos cuantiles se utilizan para parametrizar una distribución metalog semilimitada que recorre exactamente cada uno de estos nueve cuantiles. Los QPD también se han aplicado para evaluar los riesgos del impacto de un asteroide, ^[19] la ciberseguridad, ^{[6] [20]} los sesgos en las proyecciones de la producción de los yacimientos petrolíferos en comparación con la producción observada después del hecho, ^[21] y las futuras proyecciones de la población canadiense basadas en sobre la combinación de puntos de vista probabilísticos de múltiples expertos. ^[22] Consulte las distribuciones metalog y Keelin (2016) ^[5] para aplicaciones adicionales de la distribución metalog.

enlaces externos

• Distribuciones Metalog, www.metalogs.org

Referencias

1. Johnson NL, Kotz S, Balakrishnan N. Distribuciones univariadas continuas, volumen 1, segunda edición, John Wiley & Sons, Ltd, 1994, págs.
2. Johnson, Países Bajos (1949). "Sistemas de curvas de frecuencia generadas por métodos de traducción". Biometrika . 36 (1/2): 149-176. doi :10.2307/2332539. JSTOR  2332539. PMID  18132090.
3. Tadikamalla, Pandu R.; Johnson, Norman L. (1982). "Sistemas de Curvas de Frecuencia Generadas por Transformaciones de Variables Logísticas". Biometrika . 69 (2): 461–465. doi :10.1093/biomet/69.2.461. JSTOR  2335422.
4. Keelin, Thomas W.; Powley, Bradford W. (2011). "Distribuciones parametrizadas por cuantiles". Análisis de decisión . 8 (3): 206–219. doi :10.1287/deca.1110.0213.
5. Keelin, Thomas W. (2016). "Las distribuciones de Metalog". Análisis de decisión . 13 (4): 243–277. doi :10.1287/deca.2016.0338.
6. Faber, Isaac Justin; Paté-Cornell, M. Elisabeth; Lin, Herbert; Shachter, Ross D. (2019). Gestión de riesgos cibernéticos: advertencias de amenazas generadas por IA (Tesis). Universidad Stanford.
7. Keelin, Thomas W. (2016). "Las distribuciones de Metalog". Análisis de decisión . 13 (4). Tabla 8. doi :10.1287/deca.2016.0338.
8. Gilchrist, W., 2000. Modelado estadístico con funciones cuantiles. Prensa CRC.
9. Keelin, Thomas W. (2016). "Las distribuciones de Metalog". Análisis de decisión . 13 (4). Sección 3, págs. 249–257. doi :10.1287/deca.2016.0338.
10. Keelin, Thomas W. (2016). "Las distribuciones de Metalog". Análisis de decisión . 13 (4). Sección 4. doi :10.1287/deca.2016.0338.
11. Powley, BW (2013). "Métodos de funciones cuantiles para el análisis de decisiones". Corolario 12, p. 30. Tesis doctoral, Universidad de Stanford
12. Keelin, Thomas W.; Powley, Bradford W. (2011). "Distribuciones parametrizadas por cuantiles". Análisis de decisión . 8 (3). págs. 208-210. doi :10.1287/deca.1110.0213.
13. Keelin, Thomas W. (2016). "Las distribuciones de Metalog". Análisis de decisión . 13 (4): 253. doi :10.1287/deca.2016.0338.
14. Hadlock, Christopher C.; Bickel, J. Eric (2017). "Distribuciones parametrizadas por cuantiles de Johnson". Análisis de decisión . 14 : 35–64. doi :10.1287/deca.2016.0343.
15. Hadlock, Christopher C.; Bickel, J. Eric (2019). "El sistema de distribución parametrizado por cuantiles de Johnson generalizado". Análisis de decisión . 16 : 67–85. doi :10.1287/deca.2018.0376. S2CID  159339224.
16. Keelin, TW (2016), sección 6.2.2, págs. 271–274.
17. Keelin, TW (2016), Sección 6.1.1, Figura 10, págs. 266-267.
18. Mustafee, N. (18 de mayo de 2020). Las distribuciones metalog y sumas extremadamente precisas de lognormales en forma cerrada. Instituto de Ingenieros Eléctricos y Electrónicos (IEEE). págs. 3074–3085. ISBN 9781728132839.
19. Reinhardt, Jason C.; Chen, Xi; Liu, Wenhao; Manchev, Petar; Paté-Cornell, M. Elisabeth (2016). "Evaluación del riesgo de asteroides: un enfoque probabilístico". Análisis de riesgo . 36 (2): 244–261. Código Bib : 2016RiesgoA..36..244R. doi :10.1111/risa.12453. PMID  26215051. S2CID  23308354.
20. Wang, Jiali; Neil, Martín; Fenton, normando (2020). "Un enfoque de red bayesiano para la evaluación de riesgos de ciberseguridad que implementa y amplía el modelo FAIR". Computadoras y seguridad . 89 : 101659. doi : 10.1016/j.cose.2019.101659. S2CID  209099797.
21. Bratvold, Reidar B.; Mohus, Erlend; Petutschnig, David; Bickel, Eric (2020). "Previsión de producción: optimista y demasiado confiada, una y otra vez". Evaluación e ingeniería de yacimientos Spe . 23 (3): 0799–0810. doi :10.2118/195914-PA. S2CID  219661316.
22. Avances en la previsión demográfica (PDF) . Serie Springer sobre métodos demográficos y análisis de población. vol. 49. 2020. págs. 43–62. doi :10.1007/978-3-030-42472-5. hdl : 20.500.12657/42565. ISBN 978-3-030-42471-8. S2CID  226615299.