La paradoja de Olbers , también conocida como paradoja de la noche oscura o paradoja de Olbers y Cheseaux , es un argumento en astrofísica y cosmología física que dice que la oscuridad del cielo nocturno entra en conflicto con la suposición de un universo estático infinito y eterno . En el caso hipotético de que el universo sea estático, homogéneo a gran escala y poblado por un número infinito de estrellas , cualquier línea de visión desde la Tierra debe terminar en la superficie de una estrella y, por lo tanto, el cielo nocturno debería estar completamente iluminado y muy brillante. Esto contradice la oscuridad observada y la no uniformidad del cielo nocturno. [1]
La oscuridad del cielo nocturno es una prueba de la existencia de un universo dinámico, como el modelo del Big Bang . Ese modelo explica la falta de uniformidad del brillo observada invocando la expansión del universo , que aumenta la longitud de onda de la luz visible originada en el Big Bang hasta la escala de las microondas mediante un proceso conocido como corrimiento al rojo . El fondo de radiación de microondas resultante tiene longitudes de onda mucho más largas (milímetros en lugar de nanómetros), que parecen oscuras a simple vista y brillantes para un receptor de radio.
Se han propuesto otras explicaciones para la paradoja, pero ninguna ha tenido una amplia aceptación en la cosmología. Aunque no fue el primero en describirla, la paradoja recibe su nombre popular en honor al astrónomo alemán Heinrich Wilhelm Olbers (1758-1840).
El primero en abordar el problema del número infinito de estrellas y el calor resultante en el cosmos fue Cosmas Indicopleustes , un monje griego del siglo VI de Alejandría , quien afirma en su Topographia Christiana : "El cielo hecho de cristal sostiene el calor del Sol, la luna y el número infinito de estrellas; de lo contrario, habría estado lleno de fuego, y podría derretirse o incendiarse". [2]
La obra Darkness at Night: A Riddle of the Universe (1987) de Edward Robert Harrison da cuenta de la paradoja del cielo nocturno oscuro, considerada un problema en la historia de la ciencia. Según Harrison, el primero en concebir algo parecido a la paradoja fue Thomas Digges , quien también fue el primero en exponer el sistema copernicano en inglés y también postuló un universo infinito con infinitas estrellas. [3] Kepler también planteó el problema en 1610, y la paradoja tomó su forma madura en la obra del siglo XVIII de Halley y Cheseaux . [4] La paradoja se atribuye comúnmente al astrónomo aficionado alemán Heinrich Wilhelm Olbers , quien la describió en 1823, pero Harrison demuestra de manera convincente que Olbers estaba lejos de ser el primero en plantear el problema, ni su pensamiento al respecto fue particularmente valioso. Harrison sostiene que el primero en proponer una resolución satisfactoria de la paradoja fue Lord Kelvin , en un artículo poco conocido de 1901, [5] y que el ensayo Eureka (1848) de Edgar Allan Poe anticipó curiosamente algunos aspectos cualitativos del argumento de Kelvin: [1]
Si la sucesión de estrellas fuese infinita, el fondo del cielo nos ofrecería una luminosidad uniforme, como la que presenta la galaxia, puesto que no podría haber ningún punto en todo ese fondo en el que no existiese una estrella. La única manera, por tanto, de comprender, en semejante estado de cosas, los vacíos que nuestros telescopios encuentran en innumerables direcciones, sería suponer que la distancia del fondo invisible fuese tan inmensa que ningún rayo procedente de él hubiese podido llegar hasta nosotros todavía. [6]
La paradoja es que un universo estático, infinitamente viejo, con un número infinito de estrellas distribuidas en un espacio infinitamente grande, sería brillante en lugar de oscuro. [1]
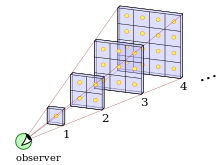
Para demostrarlo, dividimos el universo en una serie de capas concéntricas de un año luz de espesor. En cada capa habrá un número determinado de estrellas, por ejemplo, a una distancia de entre 1.000.000.000 y 1.000.000.001 años luz. Si el universo es homogéneo a gran escala, entonces habría cuatro veces más estrellas en una segunda capa entre 2.000.000.000 y 2.000.000.001 años luz. Sin embargo, la segunda capa está el doble de lejos, por lo que cada estrella que se encuentre en ella parecería un cuarto más brillante que las estrellas de la primera capa. Por lo tanto, la luz total recibida de la segunda capa es la misma que la luz total recibida de la primera capa.
De esta manera, cada capa de un espesor determinado producirá la misma cantidad neta de luz independientemente de la distancia a la que se encuentre. Es decir, la luz de cada capa se suma a la cantidad total. Por lo tanto, cuantas más capas haya, más luz habrá; y con infinitas capas, habrá un cielo nocturno brillante.
Aunque las nubes oscuras podrían obstruir la luz, estas nubes se calentarían hasta ser tan calientes como las estrellas y luego irradiarían la misma cantidad de luz.
Kepler consideró esto como un argumento a favor de un universo observable finito , o al menos de un número finito de estrellas. En la teoría de la relatividad general , todavía es posible que la paradoja se mantenga en un universo finito: [7] Aunque el cielo no sería infinitamente brillante, cada punto del cielo seguiría siendo como la superficie de una estrella.
El poeta Edgar Allan Poe sugirió en Eureka: A Prose Poem que la edad finita del universo observable resuelve la aparente paradoja. [8] Más específicamente, debido a que el universo es finitamente antiguo (más precisamente, la Era Estelífera es solo finitamente antigua) y la velocidad de la luz es finita, solo se pueden observar un número finito de estrellas desde la Tierra (aunque todo el universo puede ser infinito en el espacio). [9] [10] La densidad de estrellas dentro de este volumen finito es suficientemente baja como para que sea poco probable que cualquier línea de visión desde la Tierra alcance una estrella.
Sin embargo, la teoría del Big Bang parece introducir un nuevo problema: afirma que el cielo era mucho más brillante en el pasado, especialmente al final de la era de la recombinación , cuando se volvió transparente por primera vez. Todos los puntos del cielo local en esa época eran comparables en brillo a la superficie del Sol, debido a la alta temperatura del universo en esa época ; y la mayoría de los rayos de luz no se originarán en una estrella sino en la reliquia del Big Bang.
Este problema se soluciona con el hecho de que la teoría del Big Bang también implica la expansión del universo , que puede hacer que la energía de la luz emitida se reduzca a través del corrimiento al rojo . Más específicamente, la radiación extremadamente energética del Big Bang se ha desplazado al rojo a longitudes de onda de microondas (1100 veces la longitud de su longitud de onda original) como resultado de la expansión cósmica, y por lo tanto forma la radiación cósmica de fondo de microondas . Esto explica las densidades de luz y los niveles de energía relativamente bajos presentes en la mayor parte de nuestro cielo hoy en día a pesar de la naturaleza brillante asumida del Big Bang. El corrimiento al rojo también afecta a la luz de galaxias distantes .
El corrimiento al rojo hipotético en el modelo del Big Bang explicaría por sí mismo la oscuridad del cielo nocturno incluso si el universo fuera infinitamente viejo. En la teoría del estado estacionario, el universo es infinitamente viejo y uniforme tanto en el tiempo como en el espacio. En este modelo no hay Big Bang, pero hay estrellas y cuásares a distancias arbitrarias. La expansión del universo hace que la luz de estas estrellas y cuásares distantes se desplace al rojo, de modo que el flujo total de luz del cielo sigue siendo finito. Por lo tanto, la densidad de radiación observada (el brillo del cielo de la luz de fondo extragaláctica ) puede ser independiente de la finitud del universo. Matemáticamente, la densidad total de energía electromagnética (densidad de energía de radiación) en equilibrio termodinámico según la ley de Planck es
por ejemplo, para una temperatura de 2,7 K es 40 fJ/m 3 ... 4,5×10 −31 kg/m 3 y para una temperatura visible de 6000 K obtenemos 1 J/m 3 ... 1,1×10 −17 kg/m 3 . Pero la radiación total emitida por una estrella (u otro objeto cósmico) es como máximo igual a la energía de enlace nuclear total de los isótopos en la estrella. Para una densidad del universo observable de aproximadamente 4,6×10 −28 kg/m 3 y dada la abundancia conocida de los elementos químicos , la densidad de energía de radiación máxima correspondiente es de 9,2×10 −31 kg/m 3 , es decir, una temperatura de 3,2 K (que coincide con el valor observado para la temperatura de radiación óptica por Arthur Eddington [11] [12] ). Esto es cercano a la densidad de energía sumada del fondo cósmico de microondas (CMB) y el fondo cósmico de neutrinos . Sin embargo, el modelo de estado estable no predice la distribución angular de la temperatura del fondo de microondas con precisión (como lo hace el paradigma ΛCDM estándar). [13]
Supongamos que el universo no se estuviera expandiendo y siempre tuviera la misma densidad estelar; entonces la temperatura del universo aumentaría continuamente a medida que las estrellas emitieran más radiación. Finalmente, alcanzaría los 3000 K (que corresponden a una energía fotónica típica de 0,3 eV y, por lo tanto, a una frecuencia de 7,5×10 13 Hz ), y los fotones comenzarían a ser absorbidos por el plasma de hidrógeno que llena la mayor parte del universo, volviendo opaco el espacio exterior. Esta densidad de radiación máxima corresponde a aproximadamente1,2 × 10 17 eV/ m3 =2,1 × 10 −19 kg/m 3 , que es mucho mayor que el valor observado de4,7 × 10 −31 kg/m 3 . [4] Por lo tanto, el cielo es aproximadamente quinientos mil millones de veces más oscuro de lo que sería si el universo no se estuviera expandiendo ni fuera demasiado joven para haber alcanzado aún el equilibrio. Sin embargo, observaciones recientes que aumentan el límite inferior del número de galaxias sugieren que la absorción de rayos ultravioleta por el hidrógeno y la reemisión en longitudes de onda cercanas al infrarrojo (no visibles) también desempeñan un papel. [14]
Una resolución diferente, que no se basa en la teoría del Big Bang, fue propuesta por primera vez por Carl Charlier en 1908 y redescubierta más tarde por Benoît Mandelbrot en 1974. [ cita requerida ] Ambos postularon que si las estrellas en el universo estuvieran distribuidas en una cosmología fractal jerárquica (por ejemplo, similar al polvo de Cantor ) —la densidad promedio de cualquier región disminuye a medida que la región considerada aumenta— no sería necesario confiar en la teoría del Big Bang para explicar la paradoja de Olbers. Este modelo no descartaría un Big Bang, pero permitiría un cielo oscuro incluso si el Big Bang no hubiera ocurrido. [ cita requerida ]
Matemáticamente, la luz recibida de las estrellas en función de la distancia entre ellas en un cosmos fractal hipotético es [ cita requerida ]
dónde:
La función de luminosidad desde una distancia dada L ( r ) N ( r ) determina si la luz recibida es finita o infinita. Para cualquier luminosidad desde una distancia dada L ( r ) N ( r ) proporcional a r a , es infinita para a ≥ −1 pero finita para a < −1. Entonces, si L ( r ) es proporcional a r −2 , entonces para que sea finito, N ( r ) debe ser proporcional a r b , donde b < 1. Para b = 1, el número de estrellas en un radio dado es proporcional a ese radio. Cuando se integra sobre el radio, esto implica que para b = 1, el número total de estrellas es proporcional a r 2 . Esto correspondería a una dimensión fractal de 2. Por lo tanto, la dimensión fractal del universo tendría que ser menor que 2 para que esta explicación funcione.
Esta explicación no es ampliamente aceptada entre los cosmólogos, ya que la evidencia sugiere que la dimensión fractal del universo es al menos 2. [15] [16] [17] Además, la mayoría de los cosmólogos aceptan el principio cosmológico , [ cita requerida ] que supone que la materia a escala de miles de millones de años luz se distribuye isótropamente . Por el contrario, la cosmología fractal requiere una distribución anisotrópica de la materia en las escalas más grandes.
El puritano Thomas Digges (1546-1595?) fue el primer inglés que ofreció una defensa de la teoría copernicana. ... Junto con el relato de Digges hay un diagrama del universo que representa el sistema heliocéntrico rodeado por el orbe de estrellas fijas, descrito por Digges como infinitamente extendido en todas las dimensiones.
La simple observación de que el cielo nocturno es oscuro permite extraer conclusiones de gran alcance sobre la estructura a gran escala del universo, como ya habían descubierto J. Kepler (1610), E. Halley (1720), J.-P. Loy de Chesaux (1744) y H. W. M. Olbers (1826).
{{cite book}}: |work=ignorado ( ayuda )