Notación causal

Notación para expresar causa y efecto

La notación causal es la notación utilizada para expresar causa y efecto.

En la naturaleza y en las sociedades humanas, muchos fenómenos tienen relaciones causales en las que un fenómeno A (una causa) impacta en otro fenómeno B (un efecto). Establecer relaciones causales es el objetivo de muchos estudios científicos en campos que abarcan desde la biología ^[1] y la física ^[2] hasta las ciencias sociales y la economía ^[3] . También es un tema de análisis de accidentes ^[4] y puede considerarse un prerrequisito para la formulación de políticas efectivas.

Para describir las relaciones causales entre fenómenos, son comunes las notaciones visuales no cuantitativas, como las flechas, por ejemplo, en el ciclo del nitrógeno o en muchos libros de texto de química ^{[5] [6]} y matemáticas ^[7] . También se utilizan convenciones matemáticas, como trazar una variable independiente en un eje horizontal y una variable dependiente en un eje vertical ^[8] , o la notación para indicar que una cantidad " " es una variable dependiente que es una función de una variable independiente " ". ^[9] Las relaciones causales también se describen utilizando expresiones matemáticas cuantitativas. ^[10] (Ver la sección Notaciones). ${\displaystyle y=f(x)}$ ${\displaystyle y}$ ${\displaystyle x}$

Los siguientes ejemplos ilustran distintos tipos de relaciones causales. A continuación se presentan distintas notaciones que se utilizan para representarlas.

Ejemplos

Lo que sigue no supone necesariamente la convención por la cual denota una variable independiente y denota una función de la variable independiente . En cambio, y denotan dos cantidades con una relación causal desconocida a priori, que pueden relacionarse mediante una expresión matemática. ${\displaystyle y}$ ${\displaystyle f(y)}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle f(y)}$

Ejemplo de ecosistema: correlación sin causalidad

Imaginemos que la cantidad de días con temperaturas por debajo de un grado Celsius, , hace que se forme hielo en un lago, , y hace que los osos entren en hibernación . Aunque no causa y viceversa, se puede escribir una ecuación que relacione y . Esta ecuación se puede utilizar para calcular con éxito la cantidad de osos que hibernan , dada la superficie del lago cubierta por hielo. Sin embargo, derretir el hielo en una región del lago vertiéndole sal, no hará que los osos salgan de la hibernación. Tampoco despertar a los osos molestándolos físicamente hará que el hielo se derrita. En este caso, las dos cantidades y son causadas por una variable de confusión (la temperatura exterior), pero no entre sí. y están relacionadas por correlación sin causalidad. ${\displaystyle y}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle y}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$

Ejemplo de física: una relación causal unidireccional

Supongamos que se construye un sistema ideal de energía solar de modo que, si hace sol y el sol proporciona una intensidad de vatios que incide sobre un panel solar de m durante segundos, un motor eléctrico levanta una piedra de kg en metros. De manera más general, suponemos que el sistema se describe mediante la siguiente expresión: ${\displaystyle I}$ ${\displaystyle 100}$ ${\displaystyle 1}$ ${\displaystyle ^{2}}$ ${\displaystyle 10~}$ ${\displaystyle 2}$ ${\displaystyle 50}$ ${\displaystyle h(I)}$

${\displaystyle I\times A\times t=m\times g\times h~}$,

donde representa la intensidad de la luz solar (J s m ), representa el área de la superficie del panel solar (m ), representa el tiempo (s), representa la masa (kg), representa la aceleración debida a la gravedad de la Tierra ( m s ), y representa la altura a la que se eleva la roca (m). ${\displaystyle I}$ ${\displaystyle \cdot }$ ${\displaystyle ^{-1}}$ ${\displaystyle \cdot }$ ${\displaystyle ^{-2}}$ ${\displaystyle A}$ ${\displaystyle ^{2}}$ ${\displaystyle t}$ ${\displaystyle m}$ ${\displaystyle g}$ ${\displaystyle 9.8}$ ${\displaystyle \cdot }$ ${\displaystyle ^{-2}}$ ${\displaystyle h}$

En este ejemplo, el hecho de que haya sol y haya una intensidad de luz , hace que la piedra se eleve , no al revés; levantar la piedra (aumentar ) no dará como resultado que se encienda el sol para iluminar el panel solar (un aumento de ). La relación causal entre y es unidireccional. ${\displaystyle I}$ ${\displaystyle h(I)}$ ${\displaystyle h(I)}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle h(I)}$

Ejemplo de medicina: dos causas para un único resultado

Se sabe que fumar , y la exposición al amianto , son causas de cáncer. Se puede escribir una ecuación para describir una carcinogenicidad equivalente entre la cantidad de cigarrillos que fuma una persona, y la cantidad de gramos de amianto que inhala, . En este caso, ni causa ni causa , pero ambas tienen un resultado común. ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle y}$ ${\displaystyle f(y)=g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$

Ejemplo de trueque: una relación causal bidireccional

Consideremos una economía basada en el trueque donde el número de vacas que uno posee tiene un valor medido en una moneda estándar de pollos, . Además, el número de barriles de petróleo que uno posee tiene un valor que puede medirse en pollos, . Si existe un mercado donde las vacas pueden intercambiarse por pollos que a su vez pueden intercambiarse por barriles de petróleo, uno puede escribir una ecuación para describir la relación de valor entre vacas y barriles de petróleo . Supongamos que un individuo en esta economía siempre mantiene la mitad de su valor en forma de vacas y la otra mitad en forma de barriles de petróleo. Luego, aumentar su número de vacas al ofrecerles 4 vacas, eventualmente conducirá a un aumento en su número de barriles de petróleo , o viceversa. En este caso, la igualdad matemática describe una relación causal bidireccional. ${\displaystyle C}$ ${\displaystyle y}$ ${\displaystyle B}$ ${\displaystyle y}$ ${\displaystyle C(y)=B(y)}$ ${\displaystyle C}$ ${\displaystyle B}$ ${\displaystyle C(y)}$ ${\displaystyle B(y)}$ ${\displaystyle C(y)=B(y)}$

Notaciones

Reacciones químicas

En química, muchas reacciones químicas son reversibles y se describen mediante ecuaciones que tienden hacia un equilibrio químico dinámico . En estas reacciones, la adición de un reactivo o un producto hace que la reacción se produzca produciendo más producto o más reactivo, respectivamente. Es habitual dibujar flechas de tipo arpón en lugar de un signo igual, ⇌, para indicar la naturaleza reversible de la reacción y la relación causal dinámica entre reactivos y productos. ^{[5] [6]}

Estadísticas: Notación Do

El cálculo do , y en concreto el operador do, se utiliza para describir relaciones causales en el lenguaje de la probabilidad. Una notación utilizada en el cálculo do es, por ejemplo: ^[11]

${\displaystyle P(Y|do(X))=P(Y)~}$,

que puede leerse como: “la probabilidad de que, dado que usted hace ”. La expresión anterior describe el caso donde es independiente de cualquier cosa que se le haga a . ^[10] Especifica que no existe una relación causal unidireccional donde las causas . ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle Y}$

Diagramas causales

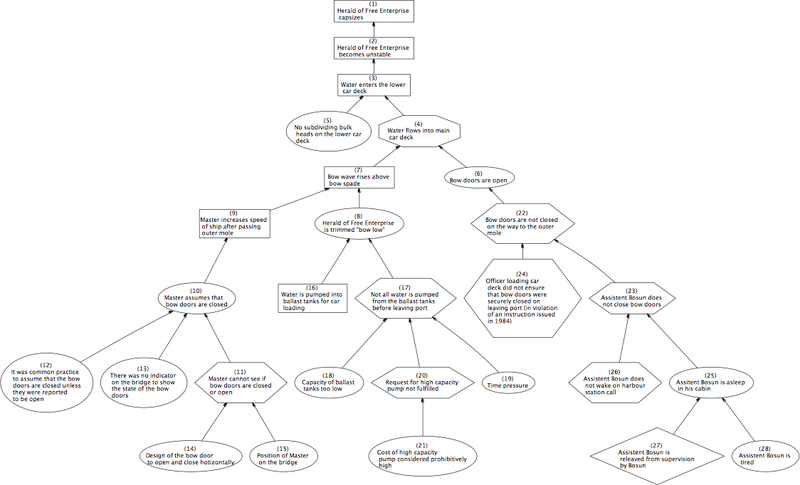
Un diagrama causal consiste en un conjunto de nodos que pueden estar interconectados o no por flechas. Las flechas entre nodos denotan relaciones causales y la flecha apunta de la causa al efecto. Existen varias formas de diagramas causales, incluidos los diagramas de Ishikawa , los gráficos acíclicos dirigidos , los diagramas de bucle causal ^[10] y los gráficos de por qué-por qué (WBG). La imagen a continuación muestra un gráfico de por qué-por qué parcial utilizado para analizar el naufragio del Herald of Free Enterprise .

Gráfico parcial de por qué y por qué del naufragio del Herald of Free Enterprise

Patrones de unión

Los patrones de unión se pueden utilizar para describir la estructura gráfica de las redes bayesianas. Los tres patrones posibles permitidos en un gráfico acíclico dirigido (DAG) de 3 nodos incluyen:

Notación de igualdad causal

Existen varias formas de relaciones causales. Por ejemplo, dos cantidades y pueden ser causadas por una variable de confusión , pero no entre sí. Imaginemos una huelga de basura en una gran ciudad, , provoca un aumento del olor a basura y un aumento de la población de ratas . Aunque no causa y viceversa, se puede escribir una ecuación que relacione y . La siguiente tabla contiene notación que representa una variedad de formas en las que , y pueden estar relacionadas entre sí. ^[12] ${\displaystyle a(s)}$ ${\displaystyle b(s)}$ ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle a(s)}$ ${\displaystyle b(s)}$ ${\displaystyle b(s)}$ ${\displaystyle a(s)}$ ${\displaystyle b(s)}$ ${\displaystyle a(s)}$ ${\displaystyle s}$ ${\displaystyle a(s)}$ ${\displaystyle b(s)}$

Se debe suponer que una relación entre dos ecuaciones con sentidos idénticos de causalidad (como , y ) es de correlación pura a menos que se demuestre que ambas expresiones son igualdades causales bidireccionales. En ese caso, la relación causal general entre y es causal bidireccional. ${\displaystyle s~{\overset {\rightarrow }{=}}~a\left(s\right)}$ ${\displaystyle s~{\overset {\rightarrow }{=}}~b\left(s\right)}$ ${\displaystyle b(s)}$ ${\displaystyle a(s)}$

Referencias

1. Marshall, Barry J; Warren, J. Robin (junio de 1984). "Bacilos curvos no identificados en el estómago de pacientes con gastritis y úlcera péptica". The Lancet . 323 (8390): 1311–1315. doi :10.1016/S0140-6736(84)91816-6. PMID  6145023. S2CID  10066001.
2. Aspect, Alain; Grangier, Philippe; Roger, Gérard (12 de julio de 1982). "Realización experimental del experimento de Einstein-Podolsky-Rosen-Bohm: una nueva violación de las desigualdades de Bell". Physical Review Letters . 49 (2): 91–94. Código Bibliográfico :1982PhRvL..49...91A. doi : 10.1103/PhysRevLett.49.91 .
3. Fischer, Stanley; Easterly, William (1990). "La economía de la restricción presupuestaria del gobierno". The World Bank Research Observer . 5 (2): 127–142. CiteSeerX 10.1.1.1009.4220 . doi :10.1093/wbro/5.2.127. 
4. Ladkin, Peter; Loer, Karsten (abril de 1998). Análisis de accidentes de aviación mediante análisis WB: una aplicación del razonamiento multimodal (PDF) . Simposio de primavera. Asociación para el avance de la inteligencia artificial . Archivado desde el original (PDF) el 21 de diciembre de 2022.
5. Bruice, Paula Yurkanis (2007). Química orgánica (5.ª ed.). Pearson Prentice Hall Upper Saddle River, NJ. pág. 44,45. ISBN 978-0-13-196316-0.
6. Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey; Madura, Jeffry D. (2007). Principios de química general y aplicaciones modernas (novena edición). Pearson Prentice Hall Upper Saddle River, NJ. págs. 573–650. ISBN 978-0-13-149330-8.
7. B. George, George (2007). Cálculo de Thomas (11.ª ed.). Pearson. pág. 20. ISBN 978-0-321-18558-7.
8. Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey; Madura, Jeffry D. (2007). Principios de química general y aplicaciones modernas (novena edición). Pearson Prentice Hall Upper Saddle River, NJ. pág. 575. ISBN 978-0-13-149330-8.
9. B. George, George (2007). Cálculo de Thomas (11.ª ed.). Pearson. pág. 19. ISBN 978-0-321-18558-7.
10. Pearl, Judea ; Mackenzie, Dana (15 de mayo de 2018). El libro del por qué: la nueva ciencia de la causa y el efecto. Basic Books. ISBN 9780465097616.
11. {{Hitchcock, Christopher, "Modelos causales", The Stanford Encyclopedia of Philosophy (edición de primavera de 2023), Edward N. Zalta y Uri Nodelman (eds.), URL = <https://plato.stanford.edu/archives/spr2023/entries/causal-models/>}}
12. Van Horne N. y Mukherjee M. Descripción mejorada de iones atrapados como un sistema electromecánico modular, J. Appl. Phys. 135, 154401 (2024)