En el procesamiento de imágenes , un núcleo , una matriz de convolución o una máscara es una pequeña matriz que se utiliza para difuminar, enfocar, realzar, detectar bordes y más. Esto se logra haciendo una convolución entre el núcleo y una imagen . O, más simplemente, cuando cada píxel de la imagen de salida es una función de los píxeles cercanos (incluido él mismo) en la imagen de entrada, el núcleo es esa función.
La expresión general de una convolución es
donde es la imagen filtrada, es la imagen original, es el núcleo del filtro. Cada elemento del núcleo del filtro es considerado por y .
Dependiendo de los valores de los elementos, un núcleo puede provocar una amplia gama de efectos:
Los anteriores son solo algunos ejemplos de efectos que se pueden lograr convolucionando núcleos e imágenes.
El origen es la posición del núcleo que está por encima (conceptualmente) del píxel de salida actual. Puede estar fuera del núcleo real, aunque normalmente corresponde a uno de los elementos del núcleo. En el caso de un núcleo simétrico, el origen suele ser el elemento central.
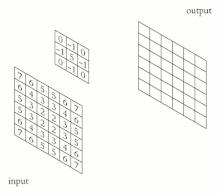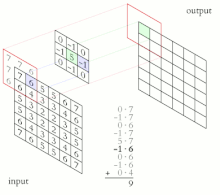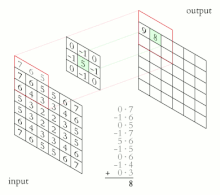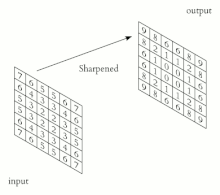
La convolución es el proceso de sumar cada elemento de la imagen a sus vecinos locales, ponderados por el núcleo. Esto está relacionado con una forma de convolución matemática . La operación matricial que se realiza (convolución) no es una multiplicación matricial tradicional, a pesar de que también se denota con *.
Por ejemplo, si tenemos dos matrices de tres por tres, la primera un núcleo y la segunda un fragmento de imagen, la convolución es el proceso de invertir tanto las filas como las columnas del núcleo y multiplicar las entradas localmente similares y sumar. El elemento en las coordenadas [2, 2] (es decir, el elemento central) de la imagen resultante sería una combinación ponderada de todas las entradas de la matriz de imagen, con pesos dados por el núcleo:
Las otras entradas tendrían una ponderación similar, donde posicionamos el centro del núcleo en cada uno de los puntos límite de la imagen y calculamos una suma ponderada.
Los valores de un píxel determinado en la imagen de salida se calculan multiplicando cada valor de kernel por los valores de píxel correspondientes de la imagen de entrada. Esto se puede describir algorítmicamente con el siguiente pseudocódigo:
para cada fila de imagen en la imagen de entrada : para cada píxel en la fila de imagen : Poner el acumulador a cero para cada fila del kernel en el kernel : para cada elemento en la fila del kernel : Si la posición del elemento corresponde* a la posición del píxel , entonces multiplica el valor del elemento correspondiente* al valor del píxel y suma el resultado al acumulador . Establecer el píxel de la imagen de salida en el acumulador
Si el núcleo es simétrico, coloque el centro (origen) del núcleo en el píxel actual. El núcleo se superpondrá a los píxeles vecinos alrededor del origen. Cada elemento del núcleo debe multiplicarse por el valor del píxel con el que se superpone y todos los valores obtenidos deben sumarse. Esta suma resultante será el nuevo valor para el píxel actual que se superpone actualmente con el centro del núcleo.
Si el núcleo no es simétrico, debe invertirse tanto alrededor de su eje horizontal como de su eje vertical antes de calcular la convolución como se indicó anteriormente. [1]
La forma general para la convolución matricial es
La convolución del núcleo generalmente requiere valores de píxeles fuera de los límites de la imagen. Existen diversos métodos para manejar los bordes de la imagen.
La normalización se define como la división de cada elemento del núcleo por la suma de todos los elementos del núcleo, de modo que la suma de los elementos de un núcleo normalizado sea la unidad. Esto garantizará que el píxel promedio de la imagen modificada sea tan brillante como el píxel promedio de la imagen original.
Los algoritmos de convolución rápida incluyen:
La convolución 2D con un núcleo M × N requiere M × N multiplicaciones para cada muestra (píxel). Si el núcleo es separable, entonces el cálculo se puede reducir a M + N multiplicaciones. El uso de convoluciones separables puede reducir significativamente el cálculo al realizar la convolución 1D dos veces en lugar de una convolución 2D. [2]
Aquí se muestra una implementación de convolución concreta realizada con el lenguaje de sombreado GLSL :
// autor: csblo // Trabajo realizado simplemente consultando: // https://en.wikipedia.org/wiki/Kernel_(image_processing)/Kernel_(image_processing)// Definir núcleos #define identidad mat3(0, 0, 0, 0, 1, 0, 0, 0, 0) #define arista0 mat3(1, 0, -1, 0, 0, 0, -1, 0, 1) #define arista1 mat3(0, 1, 0, 1, -4, 1, 0, 1, 0) #define arista2 mat3(-1, -1, -1, -1, 8, -1, -1, -1, -1) #define nitidez mat3(0, -1, 0, -1, 5, -1, 0, -1, 0) #define desenfoque de caja mat3(1, 1, 1, 1, 1, 1, 1, 1, 1) * 0.1111 #define desenfoque gaussiano mat3(1, 2, 1, 2, 4, 2, 1, 2, 1) * 0.0625 #define el tapete de relieve3(-2, -1, 0, -1, 1, 1, 0, 1, 2)// Encuentra la coordenada del elemento de la matriz a partir del índice vec2 kpos ( int index ) { return vec2 [ 9 ] ( vec2 ( - 1 , - 1 ), vec2 ( 0 , - 1 ), vec2 ( 1 , - 1 ) , vec2 ( - 1 , 0 ), vec2 ( 0 , 0 ), vec2 ( 1 , 0 ), vec2 ( - 1 , 1 ), vec2 ( 0 , 1 ), vec2 ( 1 , 1 ) )[ index ] / iResolution . xy ; } // Extrae la región de dimensión 3x3 del sampler centrado en uv // sampler: muestreador de textura // uv: coordenadas actuales en el sampler // retorna: una matriz de mat3, cada índice corresponde a un canal de color mat3 [ 3 ] region3x3 ( sampler2D sampler , vec2 uv ) { // Crea cada píxel para la región vec4 [ 9 ] region ; for ( int i = 0 ; i < 9 ; i ++ ) region [ i ] = texture ( sampler , uv + kpos ( i )); // Crea una región 3x3 con 3 canales de color (rojo, verde, azul) mat3 [ 3 ] mRegion ; for ( int i = 0 ; i < 3 ; i ++ ) mRegion [ i ] = mat3 ( región [ 0 ][ i ], región [ 1 ][ i ], región [ 2 ][ i ], región [ 3 ][ i ], región [ 4 ][ i ], región [ 5 ][ i ], región [ 6 ][ i ], región [ 7 ][ i ], región [ 8 ][ i ] ); return mRegion ; } // Convolucionar una textura con kernel // kernel: kernel usado para convolución // sampler: muestreador de textura // uv: coordenadas actuales en el muestreador vec3 convolution ( mat3 kernel , sampler2D sampler , vec2 uv ) { vec3 fragment ; // Extraer una región 3x3 centrada en uv mat3 [ 3 ] region = region3x3 ( sampler , uv ); // para cada canal de color de region for ( int i = 0 ; i < 3 ; i ++ ) { // obtener el canal de región mat3 rc = region [ i ]; // multiplicación componente por componente de kernel por canal de región mat3 c = matrixCompMult ( kernel , rc ); // suma cada componente de la matriz float r = c [ 0 ][ 0 ] + c [ 1 ][ 0 ] + c [ 2 ][ 0 ] + c [ 0 ][ 1 ] + c [ 1 ][ 1 ] + c [ 2 ][ 1 ] + c [ 0 ][ 2 ] + c [ 1 ][ 2 ] + c [ 2 ][ 2 ]; // para el fragmento en el canal i, establece el resultado fragment [ i ] = r ; } return fragment ; } void mainImage ( out vec4 fragColor , in vec2 fragCoord ) { // Coordenadas de píxeles normalizadas (de 0 a 1) vec2 uv = fragCoord / iResolution.xy ; // Núcleo de convolución con textura vec3 col = convolution ( emboss , iChannel0 , uv ); // Salida a pantalla fragColor = vec4 ( col , 1.0 ); }