La red del sistema nervioso humano está compuesta por nodos (por ejemplo, neuronas) que están conectados por enlaces (por ejemplo, sinapsis). La conectividad puede verse anatómicamente, funcionalmente o electrofisiológicamente . Estos se presentan en varios artículos de Wikipedia que incluyen Conexionismo (también conocido como Procesamiento Distribuido Paralelo (PDP)), Red neuronal biológica , Red neuronal artificial (también conocida como Red neuronal ), Neurociencia computacional , así como en varios libros de Ascoli, GA (2002), [1] Sterratt, D., Graham, B., Gillies, A. y Willshaw, D. (2011), [2] Gerstner, W. y Kistler, W. (2002), [3] y David Rumelhart , McClelland, JL y PDP Research Group (1986) [4] entre otros. El enfoque de este artículo es una visión integral del modelado de una red neuronal (técnicamente red neuronal basada en el modelo de neurona). Una vez elegido un enfoque basado en la perspectiva y la conectividad, se desarrollan los modelos a nivel microscópico (iones y neuronas), mesoscópico (funcional o poblacional) o macroscópico (sistema). El modelado computacional se refiere a los modelos que se desarrollan utilizando herramientas informáticas.
El sistema nervioso está formado por redes formadas por neuronas y sinapsis conectadas a los tejidos y que los controlan, además de influir en los pensamientos y el comportamiento humanos. Al modelar las redes neuronales del sistema nervioso, hay que tener en cuenta muchos factores. El cerebro y la red neuronal deben considerarse como un sistema de firmware integrado y autónomo que incluye hardware (órganos), software (programas), memoria (a corto y largo plazo), base de datos (centralizada y distribuida) y una red compleja de elementos activos (como neuronas, sinapsis y tejidos) y elementos pasivos (como partes del sistema visual y auditivo) que transportan información dentro y fuera del cuerpo. [ cita requerida ]
Aunque se han desarrollado y utilizado sistemas informáticos muy sofisticados en todos los ámbitos de la vida, no se acercan en absoluto a las capacidades de hardware y software del sistema humano. Por ello, los científicos han trabajado para comprender el sistema operativo humano y tratar de simular sus funcionalidades. Para lograrlo, es necesario modelar sus componentes y funciones y validar su rendimiento con la vida real. Los modelos computacionales de un sistema nervioso bien simulado permiten aprender sobre él y aplicarlo a la solución de problemas de la vida real. [ cita requerida ]
Se ha planteado la hipótesis de que la unidad biológica elemental es una célula activa, llamada neurona, y que la máquina humana está dirigida por una vasta red que conecta estas neuronas, llamada red neuronal. [5] La red neuronal está integrada con los órganos humanos para formar la máquina humana que comprende el sistema nervioso. [ cita requerida ]
La unidad estructural básica de la red neuronal es la conectividad de una neurona con otra a través de una unión activa, llamada sinapsis. Las neuronas de características muy divergentes están conectadas entre sí a través de sinapsis, cuyas características también son de diversas propiedades químicas y eléctricas. Al presentar una visión integral de todos los posibles modelos del cerebro y la red neuronal, un enfoque es organizar el material en función de las características de las redes y los objetivos que deben lograrse. Estos últimos podrían ser para comprender mejor el cerebro y el sistema nervioso o para aplicar el conocimiento obtenido del sistema nervioso total o parcial a aplicaciones del mundo real como la inteligencia artificial , la neuroética o las mejoras en la ciencia médica para la sociedad.
En una representación de alto nivel, las neuronas pueden verse como conectadas a otras neuronas para formar una red neuronal de una de tres maneras. Una red específica puede representarse como una red conectada fisiológicamente (o anatómicamente) y modelarse de esa manera. Hay varios enfoques para esto (ver Ascoli, GA (2002) [1] Sporns, O. (2007), [6] Connectionism , Rumelhart, JL, McClelland, JL y PDP Research Group (1986), [4] Arbib, MA (2007) [7] ). O bien, puede formar una red funcional que cumple una determinada función y modelarse en consecuencia (Honey, CJ, Kotter, R., Breakspear, R. y Sporns, O. (2007), [8] Arbib, MA (2007) [7] ). Una tercera forma es plantear una hipótesis sobre el funcionamiento de los componentes biológicos del sistema neuronal mediante un modelo matemático, en forma de un conjunto de ecuaciones matemáticas. Las variables de la ecuación son algunas o todas las propiedades neurobiológicas de la entidad que se está modelando, como las dimensiones de la dendrita o la tasa de estimulación del potencial de acción a lo largo del axón en una neurona. Las ecuaciones matemáticas se resuelven utilizando técnicas computacionales y los resultados se validan con procesos de simulación o experimentales. Este enfoque de modelado se denomina neurociencia computacional. Esta metodología se utiliza para modelar componentes desde el nivel iónico hasta el nivel de sistema del cerebro. Este método es aplicable para modelar sistemas integrados de componentes biológicos que llevan señales de información de una neurona a otra a través de neuronas activas intermedias que pueden pasar la señal o crear señales nuevas o adicionales. El enfoque de la neurociencia computacional es ampliamente utilizado y se basa en dos modelos genéricos, uno de potencial de membrana celular de Goldman (1943) [9] y Hodgkin y Katz (1949), [10] y el otro basado en el modelo de Hodgkin-Huxley de potencial de acción (señal de información). [11] [12] [13] [14]
Sterratt, D., Graham, B., Gillies, A., y Willshaw, D. (2011) [2] clasifican el modelo biológico de la neurociencia en nueve niveles, desde los canales iónicos hasta el nivel del sistema nervioso, en función del tamaño y la función. La Tabla 1 se basa en esto para las redes neuronales.
Sporns, O. (2007) [6] presenta en su artículo sobre conectividad cerebral, un modelado basado en tipos estructurales y funcionales. Una red que se conecta a nivel neuronal y sináptico cae en la microescala. Si las neuronas se agrupan en poblaciones de columnas y minicolumnas, el nivel se define como mesoescala. La representación a macroescala considera la red como regiones del cerebro conectadas por vías interregionales.
Arbib, MA (2007) [7] considera en el modelo modular, una formulación jerárquica del sistema en módulos y submódulos.
La señal neuronal está formada por una corriente de pulsos eléctricos cortos de una amplitud de unos 100 milivoltios y una duración de entre 1 y 2 milisegundos (Gerstner, W. y Kistler, W. (2002) [3] Capítulo 1). Los pulsos individuales son potenciales de acción o picos y la cadena de pulsos se denomina tren de picos. El potencial de acción no contiene ninguna información. Una combinación del momento de inicio del tren de picos, la velocidad o frecuencia de los picos y el número y patrón de picos en el tren de picos determinan la codificación del contenido de información o el mensaje de la señal.
La célula neuronal tiene tres componentes: dendritas, soma y axón, como se muestra en la Figura 1. Las dendritas, que tienen la forma de un árbol con ramas, llamado pérgola, reciben el mensaje de otras neuronas con las que la neurona está conectada a través de sinapsis. El potencial de acción recibido por cada dendrita de la sinapsis se llama potencial postsináptico. La suma acumulada de los potenciales postsinápticos se alimenta al soma. Los componentes iónicos del fluido dentro y fuera mantienen la membrana celular a un potencial de reposo de aproximadamente 65 milivoltios. Cuando el potencial postsináptico acumulado excede el potencial de reposo, el cuerpo celular o soma genera un potencial de acción y se propaga a lo largo del axón. El axón puede tener una o más terminales y estas terminales transmiten neurotransmisores a las sinapsis con las que está conectada la neurona. Dependiendo del estímulo recibido por las dendritas, el soma puede generar uno o más potenciales de acción bien separados o tren de picos. Si el estímulo lleva la membrana a un potencial positivo, es una neurona excitadora; y si lleva el potencial de reposo aún más en dirección negativa, es una neurona inhibidora.

La generación del potencial de acción se denomina "disparo". La neurona que se activa descrita anteriormente se denomina neurona de impulsos. Modelaremos el circuito eléctrico de la neurona en la Sección 3.6. Hay dos tipos de neuronas de impulsos. Si el estímulo permanece por encima del nivel umbral y la salida es un tren de impulsos, se denomina modelo de neurona de integración y disparo (IF). Si la salida se modela como dependiente de la respuesta al impulso del circuito, se denomina modelo de respuesta a impulsos (SRM) (Gestner, W. (1995) [15] ).
El modelo de neuronas en descarga supone que la frecuencia (inversa de la tasa a la que se generan las descargas) del tren de descargas comienza en 0 y aumenta con la corriente de estímulo. Existe otro modelo hipotético que formula que la descarga se produce en el umbral, pero hay un salto cuántico en la frecuencia en contraste con el aumento suave de la frecuencia como en el modelo de neuronas en descarga. Este modelo se denomina modelo de velocidad. Gerstner, W. y Kistler, W. (2002), [3] y Sterratt, D., Graham, B., Gillies, A. y Willshaw, D. (2011) [2] son buenas fuentes para un tratamiento detallado de los modelos de neuronas en descarga y los modelos de neuronas de velocidad.
El concepto de red neuronal artificial (RNA) fue introducido por McCulloch, WS y Pitts, W. (1943) [16] para modelos basados en el comportamiento de neuronas biológicas. Norbert Wiener (1961) [17] le dio a este nuevo campo el nombre popular de cibernética , cuyo principio es la relación interdisciplinaria entre ingeniería, biología, sistemas de control, funciones cerebrales y ciencias de la computación. Con el avance del campo de la ciencia de la computación, la computadora de tipo von Neumann se introdujo temprano en el estudio de la neurociencia. Pero no era adecuada para el procesamiento simbólico, los cálculos no deterministas, las ejecuciones dinámicas, el procesamiento distribuido paralelo y la gestión de bases de conocimiento extensas, que son necesarias para las aplicaciones de redes neuronales biológicas; y la dirección del desarrollo de máquinas similares a la mente cambió a una máquina de aprendizaje. Desde entonces, la tecnología informática ha avanzado ampliamente y la neurociencia computacional ahora puede manejar modelos matemáticos desarrollados para redes neuronales biológicas. La investigación y el desarrollo están progresando tanto en redes neuronales artificiales como biológicas, incluidos los esfuerzos para fusionar las dos.
La "teoría trina del cerebro" McLean, P. (2003) [18] es uno de los varios modelos utilizados para teorizar la estructura organizativa del cerebro. La estructura neuronal más antigua del cerebro es el tronco encefálico o "cerebro de lagarto". La segunda fase es el cerebro límbico o paleomamífero y realiza las cuatro funciones necesarias para la supervivencia animal: luchar, alimentarse, huir y fornicar. La tercera fase es el neocórtex o cerebro neomamífero. Las funciones cognitivas superiores que distinguen a los humanos de otros animales se encuentran principalmente en la corteza. El cerebro reptil controla los músculos, el equilibrio y las funciones autónomas, como la respiración y los latidos del corazón. Esta parte del cerebro está activa, incluso en el sueño profundo. El sistema límbico incluye el hipotálamo, el hipocampo y la amígdala. El neocórtex incluye la corteza y el cerebro. Corresponde al cerebro de los primates y, específicamente, a la especie humana. Cada uno de los tres cerebros está conectado a los otros dos por medio de nervios, pero cada uno parece funcionar como su propio sistema cerebral con capacidades distintas (véase la ilustración en Cerebro triuno ).
El modelo conexionista evolucionó a partir del marco de procesamiento distribuido paralelo que formula una metateoría a partir de la cual se pueden generar modelos específicos para aplicaciones específicas. El enfoque PDP (Rumelhart, JL, McClelland, JL y PDP Research Group (1986) [4] ) es un procesamiento paralelo distribuido de muchas operaciones interrelacionadas, algo similar a lo que sucede en el sistema nervioso humano. Las entidades individuales se definen como unidades y las unidades están conectadas para formar una red. Por lo tanto, en la aplicación al sistema nervioso, una representación podría ser tal que las unidades sean las neuronas y los enlaces sean las sinapsis.
Existen tres tipos de modelos de conectividad cerebral de una red (Sporns, O. (2007) [6] ). La "conectividad anatómica (o estructural)" describe una red con enlaces anatómicos que tienen una relación específica entre "unidades" conectadas. Si las propiedades dependientes son estocásticas, se define como "conectividad funcional". La "conectividad efectiva" tiene interacciones causales entre unidades distintas en el sistema. Como se dijo anteriormente, la conectividad cerebral se puede describir en tres niveles. En el micronivel, conecta neuronas a través de sinapsis eléctricas o químicas. Una columna de neuronas se puede considerar como una unidad en el mesonivel y las regiones del cerebro que comprenden una gran cantidad de neuronas y poblaciones de neuronas como unidades en el macronivel. Los enlaces en el último caso son las vías interregionales, que forman una conectividad a gran escala.
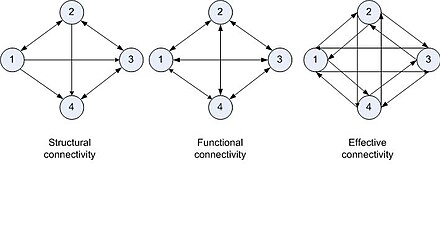
La Figura 2 muestra los tres tipos de conectividad. El análisis se realiza utilizando los grafos dirigidos (ver Sporns, O. (2007) [6] y Hilgetag, CC (2002) [19] ). En el tipo de conectividad cerebral estructural, la conectividad es un grafo disperso y dirigido. La conectividad cerebral funcional tiene grafos bidireccionales. La conectividad cerebral efectiva es bidireccional con relaciones interactivas de causa y efecto. Otra representación de la conectividad es mediante la representación matricial (ver Sporns, O. (2007) [6] ). Hilgetag, CC (2002) [19] describe el análisis computacional de la conectividad cerebral.
Arbib, MA (2007) [7] describe los modelos modulares de la siguiente manera: "Los modelos modulares del cerebro ayudan a comprender un sistema complejo al descomponerlo en módulos estructurales (por ejemplo, regiones cerebrales, capas, columnas) o módulos funcionales (esquemas) y explorar los patrones de competencia y cooperación que dan lugar a la función general". Esta definición no es la misma que la definida en la conectividad funcional. El enfoque modular tiene como objetivo construir modelos cognitivos y se encuentra, en complejidad, entre las regiones cerebrales definidas anatómicamente (definidas como macronivel en la conectividad cerebral) y el modelo computacional a nivel neuronal.
Existen tres vistas de módulos para modelado. Son (1) módulos para estructuras cerebrales, (2) módulos como esquemas y (3) módulos como interfaces. La Figura 3 presenta el diseño modular de un modelo para el control reflejo de movimientos sacádicos (Arbib, MA (2007) [7] ). Implica dos módulos principales, uno para el colículo superior (SC) y otro para el tronco encefálico. Cada uno de estos se descompone en submódulos, y cada submódulo define una matriz de neuronas definidas fisiológicamente. En la Figura 3(b), el modelo de la Figura 3(a) está integrado en un modelo mucho más grande que abarca varias regiones de la corteza cerebral (representadas por los módulos Pre-LIP Vis, Ctx., LIP, PFC y FEF), el tálamo y los ganglios basales. Si bien el modelo puede analizarse en este nivel superior de descomposición modular, necesitamos descomponer aún más los ganglios basales, BG, como se muestra en la Figura 3(c) si queremos separar el papel de la dopamina en la modulación diferencial (las 2 flechas que se muestran surgen de SNc) de las vías directas e indirectas dentro de los ganglios basales (Crowley, M. (1997) [20] ). Neural Simulation Language (NSL) se ha desarrollado para proporcionar un sistema de simulación para redes neuronales generales a gran escala. Proporciona un entorno para desarrollar un enfoque orientado a objetos para el modelado cerebral. NSL admite modelos neuronales que tienen como estructura de datos básica capas neuronales con propiedades similares y patrones de conexión similares. Los modelos desarrollados utilizando NSL están documentados en Brain Operation Database (BODB) como módulos organizados jerárquicamente que se pueden descomponer en niveles inferiores.
Como se mencionó en la Sección 2.4, el desarrollo de la red neuronal artificial (RNA), o red neuronal como se la llama ahora, comenzó como una simulación de una red neuronal biológica y terminó utilizando neuronas artificiales. El trabajo de desarrollo principal se ha dirigido a aplicaciones industriales con procesos de aprendizaje. Los problemas complejos se abordaron simplificando los supuestos. Se desarrollaron algoritmos para lograr un rendimiento relacionado con la neurología, como el aprendizaje a partir de la experiencia. Dado que los antecedentes y la descripción general se han abordado en las otras referencias internas, la discusión aquí se limita a los tipos de modelos. Los modelos están a nivel de sistema o red.
Las cuatro características principales de una ANN son la topología, el flujo de datos, los tipos de valores de entrada y las formas de activación (Meireles, MRG (2003), [21] Munakata, T. (1998) [22] ). La topología puede ser multicapa, de una sola capa o recurrente. El flujo de datos puede ser recurrente con retroalimentación o no recurrente con modelo de avance. Las entradas son binarias, bipolares o continuas. La activación es lineal, escalonada o sigmoidea. El perceptrón multicapa (MLP) es el más popular de todos los tipos, que generalmente se entrena con un algoritmo de retropropagación de errores. La salida de cada neurona está conectada a cada neurona en capas subsiguientes conectadas en cascada y sin conexiones entre neuronas en la misma capa. La Figura 4 muestra una topología MLP básica (Meireles, MRG (2003) [21] ), y una red de telecomunicaciones básica (Subramanian, M. (2010) [23] ) con la que la mayoría está familiarizada. Podemos comparar los enrutadores en los nodos de la red de telecomunicaciones con las neuronas en la tecnología MLP y los enlaces con las sinapsis.
.jpg/440px-Figure_4(a).jpg)
_Basic_MLP_technology_model.jpg/440px-Figure_4_(b)_Basic_MLP_technology_model.jpg)
La neurociencia computacional es un campo interdisciplinario que combina ingeniería, biología, sistemas de control, funciones cerebrales, ciencias físicas y ciencias de la computación. Tiene modelos de desarrollo fundamentales realizados en los niveles inferiores de iones, neuronas y sinapsis, así como la propagación de información entre neuronas. Estos modelos han establecido la tecnología habilitadora para que se desarrollen modelos de nivel superior. Se basan en actividades químicas y eléctricas en las neuronas para las cuales se generan circuitos eléctricos equivalentes. Un modelo simple para la neurona con iones de potasio predominantemente dentro de la célula e iones de sodio fuera establece un potencial eléctrico en la membrana en equilibrio, es decir, sin actividad externa, condición. Esto se llama potencial de membrana en reposo, que puede determinarse mediante la ecuación de Nernst (Nernst, W. (1888) [24] ). Un circuito eléctrico equivalente para un parche de membrana, por ejemplo un axón o una dendrita, se muestra en la Figura 5. E K y E Na son los potenciales asociados con los canales de potasio y sodio respectivamente y R K y R Na son las resistencias asociadas con ellos. C es la capacitancia de la membrana e I es la corriente de la fuente, que podría ser la fuente de prueba o la fuente de señal (potencial de acción). El potencial de reposo de los canales de potasio-sodio en una neurona es de aproximadamente -65 milivoltios.

El modelo de membrana corresponde a una pequeña sección de la membrana celular; para secciones más grandes, se puede ampliar añadiendo secciones similares, llamadas compartimentos, con valores de parámetros iguales o diferentes. Los compartimentos están conectados en cascada mediante una resistencia, llamada resistencia axial. La figura 6 muestra un modelo compartimental de una neurona que se desarrolla sobre el modelo de membrana. Las dendritas son los receptores postsinápticos que reciben entradas de otras neuronas; y el axón con una o más terminales axónicas transmite neurotransmisores a otras neuronas.

El segundo bloque de construcción es el modelo de Hodgkin-Huxley (HH) del potencial de acción. Cuando el potencial de membrana de las dendritas excede el potencial de membrana en reposo, la neurona genera un pulso que se propaga a lo largo del axón. Este pulso se denomina potencial de acción y el modelo HH es un conjunto de ecuaciones que se ajustan a los datos experimentales mediante el diseño del modelo y la elección de los valores de los parámetros.
Se pueden obtener modelos para neuronas más complejas que contengan otros tipos de iones agregando al circuito equivalente pares de resistencias y baterías adicionales para cada canal iónico. El canal iónico puede ser pasivo o activo, ya que puede estar controlado por voltaje o ser ligando. El modelo HH extendido se ha desarrollado para manejar la situación del canal activo.
Aunque hay neuronas que están conectadas fisiológicamente entre sí, la información se transmite en la mayoría de las sinapsis mediante un proceso químico a través de una hendidura. Las sinapsis también se modelan computacionalmente. El siguiente nivel de complejidad es el del flujo de potenciales de acción, que se generan, cuyo patrón contiene la información de codificación de la señal que se transmite. Básicamente, hay dos tipos de potenciales de acción, o picos como se los llama, que se generan. Uno es "integrar y disparar" (el que hemos abordado hasta ahora) y el otro, que se basa en la velocidad. Este último es un flujo cuya velocidad varía. La señal que pasa por las sinapsis se puede modelar como un proceso determinista o estocástico según la aplicación (ver Sección 3.7). Otra complicación anatómica es cuando se necesita manejar una población de neuronas, como una columna de neuronas en un sistema visionario. Esto se hace considerando el comportamiento colectivo del grupo (Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J., Sommer, FT, y Northoff, G. (2002) [25] ).
El potencial de acción o pico no lleva en sí mismo ninguna información. Es el flujo de picos, llamado tren de picos, el que lleva la información en su número y patrón de picos y el momento en que se producen. El potencial postsináptico puede ser positivo, la sinapsis excitatoria, o negativo, la sinapsis inhibidora. En el modelado, los potenciales postsinápticos recibidos por las dendritas en la neurona postsináptica se integran y cuando el potencial integrado excede el potencial de reposo, la neurona dispara un potencial de acción a lo largo de su axón. Este modelo es el modelo de integración y disparo (IF) que se mencionó en la Sección 2.3. Estrechamente relacionado con el modelo IF hay un modelo llamado modelo de respuesta a picos (SRM) (Gerstner, W. (1995) [15] páginas 738-758) que depende de la respuesta de la función de impulso convolucionada con la señal de estímulo de entrada. Esto forma una base para una gran cantidad de modelos desarrollados para redes neuronales con picos.
El modelo IF y SR del tren de picos se produce en neuronas de tipo I, en las que la tasa de picos o la frecuencia de picos de la aparición aumenta suavemente con el aumento de la corriente de estímulo comenzando desde cero. Otro fenómeno de generación de tren de picos ocurre en neuronas de tipo II, donde la activación se produce en el umbral del potencial de reposo, pero con un salto cuántico a una frecuencia distinta de cero. Se han desarrollado modelos que utilizan la tasa (frecuencia) del tren de picos y se denominan modelos basados en la tasa.
Lo importante para comprender las funciones del sistema nervioso es cómo se codifica y transporta el mensaje mediante el potencial de acción en la neurona. Existen dos teorías sobre cómo se codifica la señal que se propaga en las espigas, en cuanto a si se trata de un código de pulso o de un código de frecuencia. En la primera, es el retraso de tiempo de la primera espiga desde el momento del estímulo tal como la ve el receptor postsináptico lo que determina la codificación. En el código de frecuencia, es la frecuencia media de la espiga la que influye en la codificación. No se sabe con certeza cuál es realmente el fenómeno fisiológico real en cada caso. Sin embargo, ambos casos se pueden modelar computacionalmente y los parámetros se pueden variar para que coincidan con el resultado experimental. El modo de pulso es más complejo de modelar y Gerstner y Kistler describen numerosos modelos neuronales y modelos poblacionales detallados en las Partes I y II de Gerstner, W., & Kistler, W. (2002) [3] y el Capítulo 8 de Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011). [2] Otra característica importante asociada con el modelo SR es la plasticidad dependiente del tiempo de pico. Se basa en el postulado de Hebb sobre la plasticidad de la sinapsis, que establece que "las neuronas que se activan juntas se conectan entre sí". Esto hace que la sinapsis sea una potenciación a largo plazo (LTP) o una depresión a largo plazo (LTD). El primero es el fortalecimiento de la sinapsis entre dos neuronas si el pico postsináptico sigue temporalmente inmediatamente después del pico presináptico. El segundo es el caso si es inverso, es decir, el pico presináptico ocurre después del pico postsináptico. Gerstner, W. y Kistler, W. (2002) [3] en el Capítulo 10 y Sterratt, D., Graham, B., Gillies, A. y Willshaw, D. (2011) [2] en el Capítulo 7 analizan los diversos modelos relacionados con los modelos hebbianos sobre plasticidad y codificación.
El desafío involucrado en el desarrollo de modelos para redes pequeñas, medianas y grandes es el de reducir la complejidad haciendo suposiciones simplificadoras válidas y extendiendo el modelo neuronal de Hodgkin-Huxley apropiadamente para diseñar esos modelos (ver Capítulo 9 de Sterratt, D., Graham, B., Gillies, A., y Willshaw, D. (2011), [2] Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J., Sommer, FT, y Northoff, G. (2002), [25] y Capítulo 9 de Gerstner, W., y Kistler, W. (2002) [3] ). Los modelos de red pueden clasificarse como redes de neuronas que se propagan a través de diferentes niveles de corteza o poblaciones de neuronas interconectadas como neuronas multinivel. El posicionamiento espacial de la neurona puede ser unidimensional, bidimensional o tridimensional; las últimas se denominan redes de mundo pequeño ya que están relacionadas con la región local. La neurona puede ser excitatoria o inhibidora, pero no ambas. El diseño del modelo depende de si se trata de una neurona artificial o una neurona biológica del modelo neuronal. Se debe elegir el tipo I o el tipo II para el modo de activación. La señalización en las neuronas puede ser neuronas basadas en la frecuencia, neuronas de respuesta a picos o estimulación cerebral profunda. La red se puede diseñar como de tipo feedforward o recurrente. La red debe escalarse para las capacidades de los recursos computacionales. Los sistemas talamocorticales a gran escala se manejan de la manera del proyecto Blue Brain (Markam, H. (2006) [26] ).
No existen conceptos de modelado generalizados para modelar el desarrollo de la fisiología y morfología anatómica similar al del comportamiento de la red neuronal, que se basa en el modelo HH. Shankle, WR, Hara, J., Fallon, JH y Landing, BH (2002) [27] describen la aplicación de datos neuroanatómicos de la corteza cerebral humana en desarrollo a modelos computacionales. Sterratt, D., Graham, B., Gillies, A. y Willshaw, D. (2011) [2] discuten aspectos del sistema nervioso del modelado computacional en el desarrollo de la morfología de las células nerviosas, la fisiología celular, los patrones celulares, los patrones de dominancia ocular y la conexión entre la célula nerviosa y el músculo, y los mapas retinotópicos. Carreira-Perpinan, MA y Goodhill, GJ (2002) [28] tratan la optimización de los modelos computarizados de la corteza visual.
Con la enorme cantidad de modelos que se han creado, se han desarrollado herramientas para la difusión de la información, así como plataformas para desarrollar modelos. Existen varias herramientas generalizadas, como GENESIS, NEURON, XPP y NEOSIM, que Hucka, M. (2002) analiza. [29]