Proceso de contacto (matemáticas)

El proceso de contacto (en una red 1-D): los sitios activos se indican con círculos grises y los sitios inactivos con círculos de puntos. Los sitios activos pueden activar sitios inactivos a ambos lados de ellos a una tasa r /2 o volverse inactivos a una tasa 1.

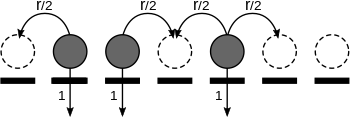
El proceso de contacto es un proceso estocástico utilizado para modelar el crecimiento de la población en el conjunto de sitios de un gráfico en el que los sitios ocupados quedan vacantes a un ritmo constante, mientras que los sitios vacantes se ocupan a un ritmo proporcional al número de sitios vecinos ocupados. Por lo tanto, si lo denotamos por la constante de proporcionalidad, cada sitio permanece ocupado durante un período de tiempo aleatorio que tiene una distribución exponencial del parámetro 1 y coloca descendientes en cada sitio vecino vacante en momentos de eventos de un parámetro del proceso de Poisson durante este período. Todos los procesos son independientes entre sí y del período aleatorio de tiempo que los sitios permanecen ocupados. El proceso de contacto también puede interpretarse como un modelo para la propagación de una infección al pensar en las partículas como una bacteria que se propaga sobre los individuos que se encuentran en los sitios de , los sitios ocupados corresponden a individuos infectados, mientras que los vacíos corresponden a los sanos. ${\displaystyle S}$ ${\displaystyle \lambda }$ ${\displaystyle \lambda }$ ${\displaystyle S}$

La principal cantidad de interés es el número de partículas en el proceso, por ejemplo , en la primera interpretación, que corresponde al número de sitios infectados en la segunda. Por tanto, el proceso sobrevive siempre que el número de partículas sea positivo en todos los tiempos, lo que corresponde al caso de que siempre haya individuos infectados en el segundo. Para cualquier grafo infinito existe un valor crítico positivo y finito de modo que si entonces la supervivencia del proceso a partir de un número finito de partículas ocurre con probabilidad positiva, mientras que si su extinción es casi segura. Tenga en cuenta que por reducción al absurdo y el teorema del mono infinito , la supervivencia del proceso es equivalente a , como , mientras que la extinción es equivalente a , como , y por lo tanto, es natural preguntar acerca de la velocidad a la que sobrevive el proceso. ${\displaystyle N_{t}}$ ${\displaystyle S}$ ${\displaystyle \lambda _{c}}$ ${\displaystyle \lambda >\lambda _{c}}$ ${\displaystyle \lambda <\lambda _{c}}$ ${\displaystyle N_{t}\to \infty }$ ${\displaystyle t\to \infty }$ ${\displaystyle N_{t}\to 0}$ ${\displaystyle t\to \infty }$ ${\displaystyle N_{t}\to \infty }$

Definición matemática

Si el estado del proceso en el momento es , entonces un sitio está ocupado, digamos por una partícula, si y vacío si . El proceso de contacto es un proceso de Markov de tiempo continuo con espacio de estados , donde generalmente es un gráfico finito o contable y un caso especial de un sistema de partículas que interactúan . Más específicamente, la dinámica del proceso de contacto básico se define por las siguientes tasas de transición: en el sitio , ${\displaystyle t}$ ${\displaystyle \xi _{t}}$ ${\displaystyle x}$ ${\displaystyle S}$ ${\displaystyle \xi _{t}(x)=1}$ ${\displaystyle \xi _{t}(x)=0}$ ${\displaystyle \{0,1\}^{S}}$ ${\displaystyle S}$ ${\displaystyle \mathbb {Z} ^{d}}$ ${\displaystyle x}$

${\displaystyle 1\rightarrow 0\quad {\text{at rate }}1,}$

${\displaystyle 0\rightarrow 1\quad {\text{at rate }}\lambda \sum _{y\,:\,y\,\sim \,x}\xi _{t}(y),}$

donde la suma es sobre todos los vecinos de in . Esto significa que cada sitio espera un tiempo exponencial con la tasa correspondiente y luego cambia (por lo que 0 se convierte en 1 y viceversa). ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle S}$

Conexión a la percolación

El proceso de contacto es un proceso estocástico que está estrechamente relacionado con la teoría de la percolación . Ted Harris (1974) señaló que el proceso de contacto sobre cuándo pueden ocurrir infecciones y recuperaciones solo en tiempos discretos corresponde a la percolación de enlaces paso a paso en el gráfico obtenido al orientar cada borde en la dirección de coordenadas crecientes. valor. ${\displaystyle \mathbb {Z} ^{d}}$ ${\displaystyle \{1,2,\ldots ,\}}$ ${\displaystyle \mathbb {Z} ^{d+1}}$

La ley de los grandes números sobre los números enteros.

Una ley de los números grandes para el número de partículas en el proceso sobre los números enteros significa informalmente que para todos los grandes , es aproximadamente igual a para alguna constante positiva . Harris (1974) demostró que, si el proceso sobrevive, entonces la tasa de crecimiento es como máximo y al menos lineal en el tiempo. Durrett (1980) demostró una ley débil de los números grandes (que el proceso converge en probabilidad ). Unos años más tarde, Durrett y Griffeath (1983) mejoraron esto hasta convertirlo en una fuerte ley de grandes números, dando una convergencia casi segura del proceso. ${\displaystyle t}$ ${\displaystyle N_{t}}$ ${\displaystyle ct}$ ${\displaystyle c=c(\lambda )}$ ${\displaystyle N_{t}}$

Extinguir en criticidad

Los procesos de contacto en todas las redes de números enteros casi seguramente desaparecen en el valor crítico. ^[1]

La conjetura de Durrett y el teorema del límite central

Durrett hizo conjeturas en artículos de estudio y notas de conferencias durante la década de 1980 y principios de la de 1990 sobre el teorema del límite central para el proceso de contacto de Harris, a saber. que, si el proceso sobrevive, entonces para todos los valores grandes , es igual y el error es igual a multiplicado por un error (aleatorio) distribuido según una distribución gaussiana estándar . ^{[2] [3] [4]} ${\displaystyle t}$ ${\displaystyle N_{t}}$ ${\displaystyle ct}$ ${\displaystyle \sigma {\sqrt {t}}}$

La conjetura de Durrett resultó ser correcta para un valor diferente de como se demostró en 2018. ^[5] ${\displaystyle \sigma }$

Referencias

1. Bezuidenhout, Carol; Grimmett, Geoffrey (1990). "El proceso de contacto crítico se extingue". Anales de probabilidad . 18 (4): 1462-1482. doi : 10.1214/aop/1176990627. JSTOR  2244329. SEÑOR  1071804.
2. Durrett, Richard (1984). "Número de percolación orientada en dos dimensiones". Los anales de la probabilidad . 12 (4): 999–1040. doi : 10.1214/aop/1176993140 .
3. Durrett, Richard. "Apuntes de conferencias sobre sistemas de partículas y percolación". Wadsworth .
4. . Durrett, Richard. "El proceso de contacto, 1974-1989". Universidad de Cornell, Instituto de Ciencias Matemáticas .
5. Tzioufas, Aquiles (2018). "El teorema del límite central para la percolación orientada supercrítica en dos dimensiones". Revista de Física Estadística . 171 (5): 802–821. arXiv : 1411.4543 . Código Bib : 2018JSP...171..802T. doi :10.1007/s10955-018-2040-y. S2CID  119174423.

Otras lecturas

• Durrett, Richard (1980). "Sobre el crecimiento de los procesos de contacto unidimensionales". Los anales de la probabilidad . 8 (5): 890–907. doi : 10.1214/aop/1176994619 .
• Durrett, Richard ; David Griffeath (1983). "Procesos de contacto supercríticos en Z". Los anales de la probabilidad . 11 (1): 1–15. doi : 10.1214/aop/1176993655 .
• Grimmett, Geoffrey (1999), Percolación, Springer
• Liggett, Thomas M. (1985). Sistemas de partículas que interactúan . Nueva York: Springer Verlag. ISBN 978-0-387-96069-2.
• Thomas M. Liggett , "Sistemas de interacción estocástica: procesos de contacto, votantes y exclusión", Springer-Verlag, 1999.