Material de Kelvin-Voigt

Modelo de material viscoelástico

Un material Kelvin-Voigt , también llamado material Voigt , es el modelo más simple de material viscoelástico que muestra propiedades típicas de la goma. Es puramente elástico en escalas de tiempo largas (deformación lenta), pero muestra resistencia adicional a la deformación rápida. El modelo fue desarrollado independientemente por el físico británico Lord Kelvin ^[1] en 1865 y por el físico alemán Woldemar Voigt ^[2] en 1890. ^[3]

Definición

Representación esquemática del modelo de Kelvin-Voigt.

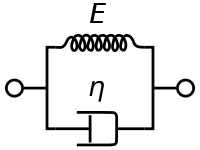
El modelo Kelvin-Voigt, también llamado modelo Voigt, está representado por un amortiguador puramente viscoso y un resorte puramente elástico conectados en paralelo como se muestra en la imagen.

Si, en cambio, conectamos estos dos elementos en serie obtenemos un modelo de material Maxwell .

Dado que los dos componentes del modelo están dispuestos en paralelo, las tensiones en cada componente son idénticas:

${\displaystyle \varepsilon _{\text{Total}}=\varepsilon _{\rm {S}}=\varepsilon _{\rm {D}}.}$

donde el subíndice D indica la tensión-deformación en el amortiguador y el subíndice S indica la tensión-deformación en el resorte. De manera similar, la tensión total será la suma de las tensiones en cada componente: ^[4]

${\displaystyle \sigma _{\text{Total}}=\sigma _{\rm {S}}+\sigma _{\rm {D}}.}$

De estas ecuaciones obtenemos que en un material Kelvin-Voigt, la tensión σ , la deformación ε y sus tasas de cambio con respecto al tiempo t están regidas por ecuaciones de la forma:

${\displaystyle \sigma (t)=E\varepsilon (t)+\eta {\frac {d\varepsilon (t)}{dt}},}$

o, en notación de puntos:

${\displaystyle \sigma =E\varepsilon +\eta {\dot {\varepsilon }},}$

donde E es un módulo de elasticidad y es la viscosidad . La ecuación se puede aplicar tanto a la tensión cortante como a la tensión normal de un material. ${\displaystyle \eta }$

Efecto de un estrés repentino

Dependencia de la deformación adimensional respecto del tiempo adimensional bajo tensión constante

Si aplicamos repentinamente una tensión constante al material Kelvin-Voigt, entonces las deformaciones se aproximarían a la deformación del material elástico puro y la diferencia decaería exponencialmente: ^[4] ${\displaystyle \sigma _{0}}$ ${\displaystyle \sigma _{0}/E}$

${\displaystyle \varepsilon (t)={\frac {\sigma _{0}}{E}}(1-e^{-t/\tau _{R}}),}$

donde t es el tiempo y es el tiempo de retardo . ${\displaystyle \tau _{R}={\frac {\eta }{E}}}$

Si liberáramos el material en el instante , entonces el elemento elástico retrasaría el material hasta que la deformación se hiciera cero. El retraso obedece a la siguiente ecuación: ${\displaystyle t_{1}}$

${\displaystyle \varepsilon (t>t_{1})=\varepsilon (t_{1})e^{-(t-t_{1})/\tau _{R}}.}$

La figura muestra la dependencia de la deformación adimensional con respecto al tiempo adimensional . En la figura, la tensión sobre el material se carga en el tiempo y se libera en el tiempo adimensional posterior . ${\displaystyle {\frac {E\varepsilon (t)}{\sigma _{0}}}}$ ${\displaystyle t/\tau _{R}}$ ${\displaystyle t=0}$ ${\displaystyle t_{1}^{*}=t_{1}/\tau _{R}}$

Dado que toda la deformación es reversible (aunque no de repente) el material Kelvin-Voigt es un sólido .

El modelo de Voigt predice la fluencia de forma más realista que el modelo de Maxwell, porque en el límite de tiempo infinito la deformación se aproxima a una constante:

${\displaystyle \lim _{t\to \infty }\varepsilon ={\frac {\sigma _{0}}{E}},}$

Mientras que un modelo de Maxwell predice una relación lineal entre la deformación y el tiempo, lo que no suele ser el caso. Aunque el modelo de Kelvin-Voigt es eficaz para predecir la fluencia, no es bueno para describir el comportamiento de relajación después de que se elimina la carga de tensión.

Módulo dinámico

El módulo dinámico complejo del material Kelvin-Voigt viene dado por:

${\displaystyle E^{\star }(\omega )=E_{0}(1+i\omega \tau ).}$

Así, los componentes reales e imaginarios del módulo dinámico se denominan módulo de almacenamiento y respectivamente: ${\displaystyle E^{\prime }}$ ${\displaystyle E^{\prime \prime }}$

${\displaystyle E^{\prime }=\Re [E^{\star }(\omega )],}$

${\displaystyle E^{\prime \prime }=\Im [E^{\star }(\omega )]=E_{0}\omega \tau .}$

Tenga en cuenta que es constante, mientras que es directamente proporcional a la frecuencia (donde la escala de tiempo es la constante de proporcionalidad). A menudo, esta constante multiplicada por la frecuencia angular se denomina módulo de pérdida . ${\displaystyle E^{\prime }}$ ${\displaystyle E^{\prime \prime }}$ ${\displaystyle \tau }$ ${\displaystyle \tau }$ ${\displaystyle \omega }$ ${\displaystyle \eta =\omega \tau }$

Referencias

1. "IV. Sobre la elasticidad y viscosidad de los metales". Actas de la Royal Society de Londres . 14 : 289–297. 1865-12-31. doi :10.1098/rspl.1865.0052. ISSN  0370-1662.
2. Voigt, Woldermar (1890). "Ueber die internale Reibung der festen Körper, insbesondere der Krystalle". Abhandlungen der Königlichen Gesellschaft von Wissenschaften zu Göttingen (en alemán). 36 : 3–47.
3. Rajagopal, KR (2009). "Una nota sobre una reevaluación y generalización del modelo de Kelvin-Voigt". Mechanics Research Communications . 36 (2): 232–235. doi :10.1016/j.mechrescom.2008.09.005.
4. Meyers, Marc André; Chawla, Krishan Kumar (1999). "Sección 13.11". Comportamiento mecánico de los materiales. Cambridge University Press. págs. 570–580. ISBN 978-1-107-39418-6.

Véase también

• Material de hamburguesas
• Modelo de Maxwell generalizado
• Material de Maxwell
• Modelo sólido lineal estándar