La matriz multirasgo-multimétodo ( MTMM ) es un enfoque para examinar la validez de constructo desarrollado por Campbell y Fiske (1959). [1] Organiza la evidencia de validez convergente y discriminante para comparar cómo se relaciona una medida con otras medidas. El enfoque conceptual ha influido en el diseño experimental y la teoría de la medición en psicología, incluidas las aplicaciones en modelos de ecuaciones estructurales.
En este enfoque se utilizan múltiples rasgos para examinar (a) rasgos similares o (b) rasgos diferentes ( constructos ), con el fin de establecer validez convergente y discriminante entre rasgos. De manera similar, en este enfoque se utilizan múltiples métodos para examinar los efectos diferenciales (o la falta de ellos) causados por la varianza específica del método. Las puntuaciones podrían estar correlacionadas porque miden rasgos similares, o porque se basan en métodos similares, o ambas cosas. Cuando las variables que se supone que miden diferentes constructos muestran una alta correlación porque se basan en métodos similares, esto a veces se describe como un problema de "varianza molesta" o "sesgo del método". [2]
Hay seis consideraciones principales al examinar la validez de un constructo a través de la matriz MTMM, que son las siguientes:
El ejemplo que se muestra a continuación proporciona una matriz prototípica y el significado de las correlaciones entre las medidas. La línea diagonal suele rellenarse con un coeficiente de fiabilidad de la medida (por ejemplo, el coeficiente alfa). Las descripciones entre corchetes [] indican lo que se espera cuando la validez del constructo (por ejemplo, depresión o ansiedad) y la validez de las medidas son todas altas.
En este ejemplo, la primera fila enumera el rasgo que se está evaluando (es decir, depresión o ansiedad), así como el método de evaluación de este rasgo (es decir, cuestionario autoinformado versus una entrevista). El término heterométodo indica que esta celda informa la correlación entre dos métodos separados. Monométodo indica que se está utilizando el mismo método en su lugar (por ejemplo, entrevista y entrevista). Heterorasgo indica que la celda se refiere a dos rasgos supuestamente diferentes. Monorasgo indica el mismo rasgo que se supone que se mide.
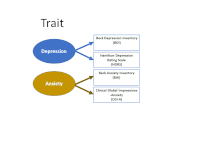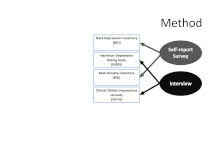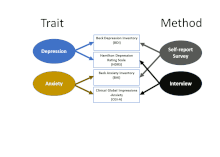
Este marco deja claro que hay al menos dos fuentes de variación que pueden influir en las puntuaciones observadas en una medida: no sólo el rasgo subyacente (que suele ser el objetivo de recopilar la medición en primer lugar), sino también el método utilizado para recopilar la medición. La matriz MTMM utiliza dos o más medidas de cada rasgo y dos o más métodos para empezar a separar las contribuciones de los diferentes factores. El primer cuadro de la figura animada muestra cómo las cuatro mediciones de la tabla están emparejadas en términos de centrarse en los "rasgos" de la depresión (BDI y HDRS) y la ansiedad (BAI y CGI-A). El segundo muestra que también están emparejadas en términos del método de origen: dos utilizan cuestionarios de autoinforme (a menudo denominados "encuestas"), y dos se basan en entrevistas (que pueden incorporar la observación directa de la comunicación y el comportamiento no verbales, así como la respuesta del entrevistado).
Con datos observados, es posible examinar la proporción de varianza compartida entre rasgos y métodos para tener una idea de cuánta varianza específica del método es inducida por el método de medición, así como también brindar una visión de cuán distinto es el rasgo, en comparación con otro rasgo.
Lo ideal sería que el rasgo fuera más importante que el método específico elegido para la medición. Por ejemplo, si una persona se considera muy deprimida según una medida, entonces otra medida de depresión también debería arrojar puntuaciones altas. Por otro lado, las personas que parecen muy deprimidas según el Inventario de Depresión de Beck no necesariamente deberían obtener puntuaciones altas de ansiedad en el Inventario de Ansiedad de Beck , ya que se supone que están midiendo diferentes constructos. Dado que los inventarios fueron escritos por la misma persona y son similares en estilo, podría haber alguna correlación, pero esta similitud en el método no debería afectar mucho a las puntuaciones, por lo que las correlaciones entre estas medidas de diferentes rasgos deberían ser bajas.
Se han utilizado diversos enfoques estadísticos para analizar los datos de la matriz MTMM. El método estándar de Campbell y Fiske se puede implementar utilizando el programa MTMM.EXE disponible en: https://web.archive.org/web/20160304173400/http://gim.med.ucla.edu/FacultyPages/Hays/utils/ También se puede utilizar el análisis factorial confirmatorio [4] debido a las complejidades de considerar todos los datos de la matriz. Sin embargo, la prueba I de Sawilowsky [5] [6] considera todos los datos de la matriz con una prueba estadística de distribución libre para la tendencia.
La prueba se realiza reduciendo los triángulos heterorasgo-heterométodo y heterorasgo-monométodo, y las diagonales de validez y confiabilidad, en una matriz de cuatro niveles. Cada nivel consta del valor mínimo, la mediana y el máximo. La hipótesis nula es que estos valores no están ordenados, lo que se prueba frente a la hipótesis alternativa de una tendencia ordenada creciente. La estadística de prueba se obtiene contando el número de inversiones (I). El valor crítico para alfa = 0,05 es 10 y para alfa = 0,01 es 14.
Uno de los modelos más utilizados para analizar datos MTMM es el modelo True Score propuesto por Saris y Andrews ( [7] ). El modelo True Score puede expresarse mediante las siguientes ecuaciones estandarizadas:
1) Y ij = r ij TS ij + e ij * donde: Y ij es la variable observada estandarizada medida con el i ésimo rasgo y el j ésimo método. r ij es el coeficiente de confiabilidad, que es igual a: r ij = σ Y ij / σ TS ij TS ij es la variable de puntuación verdadera estandarizada e ij * es el error aleatorio, que es igual a: e ij * = e ij / σ Y ij Como consecuencia: r ij 2 = 1 - σ 2 (e ij *) donde: r ij 2 es la confiabilidad
2) TS ij = v ij F i + m ij M j donde: v ij es el coeficiente de validez, que es igual a: v ij = σ F i / σ TS ij F i es el factor latente estandarizado para la i ésima variable de interés (o rasgo) m ij es el efecto del método, que es igual a: m ij = σ M j / σ TS ij M j es el factor latente estandarizado para la reacción al j ésimo método Como consecuencia: v ij 2 = 1 - m ij 2 donde: v ij 2 es la validez
3) Y ij = q ij F i + r ij m ij M j + e* donde: q ij es el coeficiente de calidad, que es igual a: q ij = r ij • v ij Como consecuencia: q ij 2 = r ij 2 • v ij 2 = σ 2 F i / σ 2 Y ij donde: q ij 2 es la calidad
Los supuestos son los siguientes:
* Los errores son aleatorios, por lo que la media de los errores es cero: µ e = E (e) = 0 * Los errores aleatorios no están correlacionados entre sí: cov (e i , e j ) = E (e i e j ) = 0 * Los errores aleatorios no están correlacionados con las variables independientes: cov (TS, e) = E (TS e) = 0 , cov (F, e) = E (F e) = 0 y cov (M, e) = E (M e) = 0 * Se supone que los factores del método no están correlacionados entre sí y con los factores de rasgo: cov (F, M) = E (FM) = 0
Por lo general, el encuestado debe responder al menos a tres medidas diferentes (es decir, rasgos) medidas utilizando al menos tres métodos diferentes. Este modelo se ha utilizado para estimar la calidad de miles de preguntas de encuestas, en particular en el marco de la Encuesta Social Europea .