Configuración (politopo)

En geometría , HSM Coxeter llamó politopo regular a un tipo especial de configuración .

Otras configuraciones en geometría son algo diferente. Estas configuraciones de politopo pueden llamarse con más precisión matrices de incidencia , donde los elementos iguales se agrupan en filas y columnas. Los politopos regulares tendrán una fila y una columna por cada elemento de k -cara , mientras que otros politopos tendrán una fila y una columna para cada tipo de k-cara por sus clases de simetría. Un politopo sin simetría tendrá una fila y una columna para cada elemento, y la matriz se llenará con 0 si los elementos no están conectados, y 1 si están conectados. Los elementos del mismo k no estarán conectados y tendrán una entrada de tabla "*". ^[1]

Cada politopo, y politopo abstracto, tiene un diagrama de Hasse que expresa estas conectividades, que pueden describirse sistemáticamente con una matriz de incidencia .

Matriz de configuración de politopos regulares

Una configuración para un politopo regular se representa mediante una matriz donde el elemento diagonal, N _i , es el número de i -caras en el politopo. Los elementos diagonales también se denominan f-vector de un politopo . El elemento no diagonal ( i ≠ j ) N _ij es el número de j -caras incidentes con cada elemento de i -cara, de modo que N _i N _ij = N _j N _ji . ^[2]

El principio se extiende generalmente a n dimensiones, donde 0 ≤ j < n .

${\displaystyle {\begin{bmatrix}{\begin{matrix}N_{0}&N_{0,1}&N_{0,2}&\cdots &N_{0,n-1}\\N_{1,0}&N_{1}&N_{1,2}&\cdots &N_{1,n-1}\\\vdots &\vdots &\vdots &&\vdots \\N_{n-1,0}&N_{n-1,1}&N_{n-1,2}&\cdots &N_{n-1}\end{matrix}}\end{bmatrix}}}$

Polígonos

Un polígono regular , símbolo de Schläfli { q }, tendrá una matriz de 2x2, con la primera fila para los vértices y la segunda fila para las aristas. El orden  g es 2 q .

${\displaystyle {\begin{bmatrix}{\begin{matrix}N_{0}&N_{01}\\N_{10}&N_{1}\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}g/2&2\\2&g/2\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}q&2\\2&q\end{matrix}}\end{bmatrix}}}$

Un n-gono general tendrá una matriz 2n x 2n, con las primeras n filas y columnas como vértices, y las últimas n filas y columnas como aristas.

Ejemplo de triangulo

Existen tres clasificaciones de simetría de un triángulo : equilátero, isósceles y escaleno. Todos ellos tienen la misma matriz de incidencia , pero la simetría permite que los vértices y las aristas se recopilen y cuenten. Estos triángulos tienen vértices etiquetados como A, B, C y aristas como a, b, c, mientras que los vértices y las aristas que se pueden mapear entre sí mediante una operación de simetría se etiquetan de manera idéntica.

Cuadriláteros

Cuadriláteros por simetría

Los cuadriláteros se pueden clasificar por simetría, cada uno con su propia matriz. Existen cuadriláteros con pares duales que tendrán la misma matriz, rotada 180 grados, con vértices y aristas invertidas. Los cuadrados y paralelogramos, y los cuadriláteros en general, son autoduales por clase, por lo que sus matrices no cambian cuando se rotan 180 grados.

Polígonos complejos

La idea también es aplicable a polígonos complejos regulares , _p { q } _r construidos en : ${\displaystyle \mathbb {C} ^{2}}$

${\displaystyle {\begin{bmatrix}{\begin{matrix}N_{0}&N_{01}\\N_{10}&N_{1}\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}g/r&r\\p&g/p\end{matrix}}\end{bmatrix}}}$

El grupo de reflexión complejo es _p [ q ] _r , orden . ^{[3] [4]} ${\displaystyle g=8/q\cdot (1/p+2/q+1/r-1)^{-2}}$

Poliedros

La idea se puede aplicar en tres dimensiones considerando incidencias de puntos, líneas y planos, o j -espacios (0 ≤ j < 3) , donde cada j -espacio incide con N _jk k - espacios ( j ≠ k ) . Escribiendo N _j para el número de j -espacios presentes, una configuración dada se puede representar por la matriz

${\displaystyle {\begin{bmatrix}{\begin{matrix}N_{0}&N_{01}&N_{02}\\N_{10}&N_{1}&N_{12}\\N_{20}&N_{21}&N_{2}\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}g/2q&q&q\\2&g/4&2\\p&p&g/2p\end{matrix}}\end{bmatrix}}}$para el símbolo de Schläfli {p,q}, con orden de grupo  g  = 4 pq /(4 − ( p  − 2)( q  − 2)).

Tetraedro

Simetrías de tetraedros

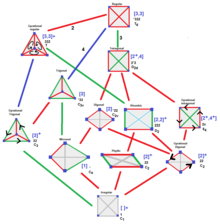
Los tetraedros tienen matrices que también se pueden agrupar por su simetría. Un tetraedro general tiene 14 filas y columnas para los 4 vértices, 6 aristas y 4 caras. Los tetraedros son autoduales y, si se rotan las matrices 180 grados (intercambiando vértices y caras), no se modificarán.

Notas

1. Klitzing, Richard. "Matrices de incidencia".
2. Coxeter, Politopos regulares complejos , pág. 117
3. Lehrer y Taylor 2009, pág. 87
4. Politopos regulares complejos, pág. 117

Referencias

• Coxeter, HSM (1948), Politopos regulares , Methuen y Co.
• Coxeter, HSM (1991), Politopos complejos regulares , Cambridge University Press, ISBN 0-521-39490-2
• Coxeter, HSM (1999), "Configuraciones autoduales y grafos regulares", La belleza de la geometría , Dover, ISBN 0-486-40919-8