En astronomía , la masa mínima es la masa calculada del límite inferior de objetos observados, como planetas , estrellas , sistemas binarios , [1] nebulosas , [2] y agujeros negros .
La masa mínima es una estadística ampliamente citada para planetas extrasolares detectados por el método de velocidad radial o espectroscopia Doppler, y se determina utilizando la función de masa binaria . Este método revela planetas midiendo cambios en el movimiento de estrellas en la línea de visión , por lo que las inclinaciones orbitales reales y las masas verdaderas de los planetas son generalmente desconocidas. [3] Esto es un resultado de la degeneración sen i .
Si se puede determinar la inclinación i , la masa real se puede obtener a partir de la masa mínima calculada utilizando la siguiente relación:

La mayoría de las estrellas no tienen sus planetas alineados y orientados de manera que se eclipsen sobre el centro de la estrella y ofrezcan al observador en la Tierra un tránsito perfecto. Es por esta razón que, cuando observamos el bamboleo de una estrella, a menudo solo podemos extrapolar una masa mínima porque no conocemos la inclinación y, por lo tanto, solo podemos calcular la parte que tira de la estrella en el plano de la esfera celeste.
Para los cuerpos que orbitan en sistemas planetarios extrasolares , una inclinación de 0° o 180° corresponde a una órbita de frente (que no se puede observar mediante la velocidad radial), mientras que una inclinación de 90° corresponde a una órbita de canto (para la cual la masa real es igual a la masa mínima). [4]
Los planetas con órbitas muy inclinadas respecto de la línea de visión desde la Tierra producen oscilaciones visibles más pequeñas y, por lo tanto, son más difíciles de detectar. Una de las ventajas del método de velocidad radial es que se puede medir directamente la excentricidad de la órbita del planeta. Una de las principales desventajas del método de velocidad radial es que solo puede estimar la masa mínima de un planeta ( ). Esto se denomina degeneración sen i . La distribución posterior del ángulo de inclinación i depende de la distribución de masa real de los planetas. [5]
Sin embargo, cuando hay varios planetas en el sistema que orbitan relativamente cerca uno del otro y tienen suficiente masa, el análisis de estabilidad orbital permite limitar la masa máxima de estos planetas. El método de velocidad radial se puede utilizar para confirmar los hallazgos realizados con el método de tránsito . Cuando se utilizan ambos métodos en combinación, se puede estimar la masa real del planeta.
Aunque la velocidad radial de la estrella sólo proporciona la masa mínima del planeta, si las líneas espectrales del planeta se pueden distinguir de las líneas espectrales de la estrella, se puede encontrar la velocidad radial del propio planeta, y esto proporciona la inclinación de la órbita del planeta. Esto permite medir la masa real del planeta. Esto también descarta los falsos positivos y también proporciona datos sobre la composición del planeta. El problema principal es que tal detección es posible sólo si el planeta orbita alrededor de una estrella relativamente brillante y si el planeta refleja o emite mucha luz. [6]
El término masa verdadera es sinónimo del término masa , pero se utiliza en astronomía para diferenciar la masa medida de un planeta de la masa mínima que se obtiene habitualmente a partir de técnicas de velocidad radial. [7] Los métodos utilizados para determinar la masa verdadera de un planeta incluyen la medición de la distancia y el período de uno de sus satélites , [8] técnicas avanzadas de astrometría que utilizan los movimientos de otros planetas en el mismo sistema estelar , [7] la combinación de técnicas de velocidad radial con observaciones de tránsito (que indican inclinaciones orbitales muy bajas), [9] y la combinación de técnicas de velocidad radial con mediciones de paralaje estelar (que también determinan inclinaciones orbitales). [10]

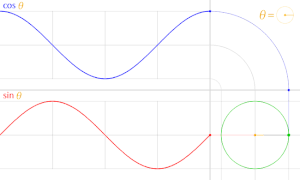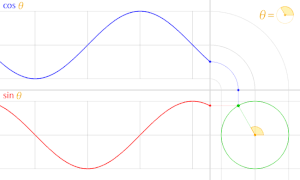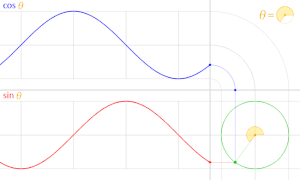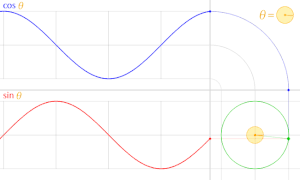
En trigonometría , un círculo unitario es el círculo de radio uno centrado en el origen (0, 0) en el sistema de coordenadas cartesianas .
Sea una línea que pasa por el origen y forma un ángulo θ con la mitad positiva del eje x , que interseca el círculo unitario. Las coordenadas x e y de este punto de intersección son iguales a cos( θ ) y sen( θ ) , respectivamente. La distancia del punto al origen es siempre 1.
Con una masa de solo 93 veces la de Júpiter ( M J ), o .09 M ☉ , AB Doradus C , compañera de AB Doradus A, es la estrella más pequeña conocida que experimenta fusión nuclear en su núcleo. [11] Para estrellas con metalicidad similar al Sol, la masa mínima teórica que puede tener la estrella, y aún así experimentar fusión en el núcleo, se estima en aproximadamente 75 M J . [12] [13] Sin embargo, cuando la metalicidad es muy baja, un estudio reciente de las estrellas más débiles encontró que el tamaño mínimo de la estrella parece ser de aproximadamente el 8,3% de la masa solar, o aproximadamente 87 M J . [13] [14] Los cuerpos más pequeños se denominan enanas marrones , que ocupan un área gris mal definida entre las estrellas y los gigantes gaseosos .