
En matemáticas , el método de Lill es un método visual para encontrar las raíces reales de un polinomio univariante de cualquier grado . [1] Fue desarrollado por el ingeniero austríaco Eduard Lill en 1867. [2] Un artículo posterior de Lill abordó el problema de las raíces complejas . [3]
El método de Lill consiste en dibujar una trayectoria de segmentos de línea recta que forman ángulos rectos , con longitudes iguales a los coeficientes del polinomio. Las raíces del polinomio se pueden encontrar como las pendientes de otras trayectorias en ángulo recto, que también conectan el inicio con el final, pero con vértices en las líneas de la primera trayectoria.

Para emplear este método, se dibuja un diagrama comenzando en el origen. Se dibuja un segmento de línea hacia la derecha según la magnitud del primer coeficiente (el coeficiente del término de mayor potencia) (de modo que, con un coeficiente negativo, el segmento terminará a la izquierda del origen). Desde el final del primer segmento, se dibuja otro segmento hacia arriba según la magnitud del segundo coeficiente, luego hacia la izquierda según la magnitud del tercero, y hacia abajo según la magnitud del cuarto, y así sucesivamente. La secuencia de direcciones (no de giros) es siempre hacia la derecha, hacia arriba, hacia la izquierda, hacia abajo y luego se repite. Por lo tanto, cada giro es en sentido contrario a las agujas del reloj. El proceso continúa para cada coeficiente del polinomio, incluidos los ceros, con coeficientes negativos "caminando hacia atrás". El punto final alcanzado, al final del segmento correspondiente al término constante de la ecuación, es el término.
Luego se lanza una línea desde el origen en algún ángulo θ , se refleja en cada segmento de línea en un ángulo recto (no necesariamente el ángulo "natural" de reflexión), y se refracta en un ángulo recto a través de la línea a través de cada segmento (incluyendo una línea para los coeficientes cero) cuando la trayectoria en ángulo no toca el segmento de línea en esa línea. [4] Las líneas verticales y horizontales se reflejan o se refractan a través de la siguiente secuencia: la línea que contiene el segmento correspondiente al coeficiente de luego de etc. Eligiendo θ de modo que la trayectoria aterrice en el término, el negativo de la tangente de θ es una raíz de este polinomio. Para cada cero real del polinomio habrá un único ángulo inicial y trayectoria que aterrizará en el término. Una cuadrática con dos raíces reales, por ejemplo, tendrá exactamente dos ángulos que satisfacen las condiciones anteriores.
Para raíces complejas, también es necesario encontrar una serie de triángulos semejantes , pero con los vértices del camino de la raíz desplazados del camino polinomial por una distancia igual a la parte imaginaria de la raíz. En este caso, el camino de la raíz no será rectangular. [5] [3]
La construcción en efecto evalúa el polinomio según el método de Horner . Para el polinomio, los valores de , , se generan sucesivamente como distancias entre los vértices del polinomio y las rutas de la raíz. Para una raíz del polinomio, el valor final es cero, por lo que el último vértice coincide con el término de la ruta del polinomio.
Una línea de solución que da una raíz es similar a la construcción de Lill para el polinomio con esa raíz eliminada, porque la construcción visual es análoga a la división sintética del polinomio por una mónica lineal (raíz) ( regla de Ruffini ).
De la simetría del diagrama se puede ver fácilmente que las raíces del polinomio invertido son los recíprocos de las raíces originales.
La construcción también se puede realizar mediante giros en el sentido de las agujas del reloj en lugar de en el sentido contrario. Cuando se interpreta una ruta mediante la otra convención, corresponde al polinomio reflejado (cada signo de coeficiente impar cambia) y se niegan las raíces.
Cuando se recorre el camino en ángulo recto en la otra dirección pero con la misma convención de dirección, corresponde al polinomio reflejado invertido y las raíces son los recíprocos negativos de las raíces originales. [4]

El método de Lill se puede utilizar con el teorema de Thales para encontrar las raíces reales de un polinomio cuadrático.
En este ejemplo con 3 x 2 + 5 x −2, los segmentos de línea del polinomio se dibujan primero en negro, como se muestra arriba. Se dibuja un círculo con el segmento de línea recta que une los puntos inicial y final formando un diámetro.
Según el teorema de Tales, el triángulo que contiene estos puntos y cualquier otro punto del círculo es un triángulo rectángulo . Las intersecciones de este círculo con el segmento medio del método de Lill, ampliadas si es necesario, definen así los dos caminos en ángulo del método de Lill, coloreados en azul y rojo.
El negativo de los gradientes de sus primeros segmentos, m , produce las raíces reales 1/3 y −2.
En 1936, Margherita Piazzola Beloch demostró cómo el método de Lill podía adaptarse para resolver ecuaciones cúbicas mediante plegado de papel . [6] Si se permiten plegados simultáneos, entonces cualquier ecuación de grado n con una raíz real puede resolverse utilizando n –2 plegados simultáneos. [7]
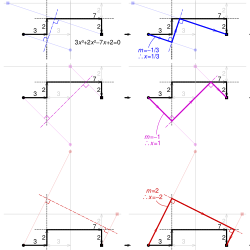
En este ejemplo con 3x 3 + 2x 2 −7x+2, primero se dibujan los segmentos de línea del polinomio en una hoja de papel (negra). Se dibujan líneas que pasan por las reflexiones de los puntos de inicio y fin en el segundo y tercer segmento, respectivamente (círculo y cuadrado tenues), y paralelas a ellos (líneas grises).
Para cada raíz, el papel se dobla hasta que el punto de inicio (círculo negro) y el punto final (cuadrado negro) se reflejan en estas líneas. El eje de reflexión (línea de puntos y rayas) define la trayectoria en ángulo correspondiente a la raíz (azul, violeta y rojo). El negativo de los gradientes de sus primeros segmentos, m , da como resultado las raíces reales 1/3, 1 y −2.