Montón binomial

Estructura de datos que actúa como una cola de prioridad

En informática , un montón binomial es una estructura de datos que actúa como una cola de prioridad . Es un ejemplo de un montón fusionable (también llamado montón combinable), ya que admite la fusión de dos montones en tiempo logarítmico. Se implementa como un montón similar a un montón binario pero utilizando una estructura de árbol especial que es diferente de los árboles binarios completos utilizados por los montones binarios. ^[1] Los montones binomiales fueron inventados en 1978 por Jean Vuillemin . ^{[1] [2]}

Montón binomial

Un montón binomial se implementa como un conjunto de árboles binomiales (compárese con un montón binario , que tiene la forma de un solo árbol binario ), que se definen recursivamente de la siguiente manera: ^[1]

• Un árbol binomial de orden 0 es un solo nodo
• Un árbol binomial de orden tiene un nodo raíz cuyos hijos son raíces de árboles binomiales de órdenes , , ..., 2, 1, 0 (en este orden). ${\displaystyle k}$ ${\displaystyle k-1}$ ${\displaystyle k-2}$

Árboles binomiales de orden 0 a 3: cada árbol tiene un nodo raíz con subárboles de todos los árboles binomiales de orden inferior, que se han resaltado. Por ejemplo, el árbol binomial de orden 3 está conectado a un árbol binomial de orden 2, 1 y 0 (resaltados en azul, verde y rojo respectivamente).

Un árbol binomial de orden tiene nodos y una altura . El nombre proviene de la forma: un árbol binomial de orden tiene nodos en profundidad y un coeficiente binomial . Debido a su estructura, un árbol binomial de orden se puede construir a partir de dos árboles de orden uniendo uno de ellos como el hijo más a la izquierda de la raíz del otro árbol. Esta característica es fundamental para la operación de fusión de un montón binomial, que es su principal ventaja sobre otros montones convencionales. ^{[1] [3]} ${\displaystyle k}$ ${\displaystyle 2^{k}}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle {\tbinom {k}{d}}}$ ${\displaystyle d}$ ${\displaystyle k}$ ${\displaystyle k-1}$

Estructura de un montón binomial

Un montón binomial se implementa como un conjunto de árboles binomiales que satisfacen las propiedades del montón binomial : ^[1]

• Cada árbol binomial en un montón obedece la propiedad del montón mínimo : la clave de un nodo es mayor o igual que la clave de su padre.
• Puede haber como máximo un árbol binomial para cada orden, incluido el orden cero.

La primera propiedad garantiza que la raíz de cada árbol binomial contenga la clave más pequeña del árbol. De ello se deduce que la clave más pequeña de todo el montón es una de las raíces. ^[1]

La segunda propiedad implica que un montón binomial con nodos consta de, como máximo, árboles binomiales, donde es el logaritmo binario . El número y los órdenes de estos árboles están determinados de forma única por el número de nodos : hay un árbol binomial por cada bit distinto de cero en la representación binaria del número . Por ejemplo, el número decimal 13 es 1101 en binario, , y, por lo tanto, un montón binomial con 13 nodos constará de tres árboles binomiales de órdenes 3, 2 y 0 (véase la figura siguiente). ^{[1] [3]} ${\displaystyle n}$ ${\displaystyle 1+\log _{2}n}$ ${\displaystyle \log _{2}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle 2^{3}+2^{2}+2^{0}}$

Ejemplo de un montón binomial que contiene 13 nodos con claves distintas. El montón consta de tres árboles binomiales con órdenes 0, 2 y 3.

La cantidad de formas diferentes en que los elementos con claves distintas se pueden organizar en un montón binomial es igual al divisor impar más grande de . Para estos números son ${\displaystyle n}$ ${\displaystyle n!}$ ${\displaystyle n=1,2,3,\dots }$

1, 1, 3, 3, 15, 45, 315, 315, 2835, 14175, ... (secuencia A049606 en la OEIS )

Si los elementos se insertan en un montón binomial en un orden uniformemente aleatorio, cada una de estas disposiciones es igualmente probable. ^[3] ${\displaystyle n}$

Implementación

Debido a que ninguna operación requiere acceso aleatorio a los nodos raíz de los árboles binomiales, las raíces de los árboles binomiales se pueden almacenar en una lista enlazada , ordenadas por orden creciente del árbol. Debido a que el número de hijos de cada nodo es variable, no funciona bien que cada nodo tenga enlaces separados a cada uno de sus hijos, como sería común en un árbol binario ; en cambio, es posible implementar este árbol utilizando enlaces desde cada nodo a su hijo de orden más alto en el árbol, y a su hermano del siguiente orden más pequeño que él. Estos punteros de hermano se pueden interpretar como los siguientes punteros en una lista enlazada de los hijos de cada nodo, pero con el orden opuesto a la lista enlazada de raíces: del orden más grande al más pequeño, en lugar de viceversa. Esta representación permite que dos árboles del mismo orden se vinculen entre sí, formando un árbol del siguiente orden más grande, en tiempo constante. ^{[1] [3]}

Unir

Para fusionar dos árboles binomiales del mismo orden, primero se compara la clave raíz. Como 7>3, el árbol negro de la izquierda (con el nodo raíz 7) se adjunta al árbol gris de la derecha (con el nodo raíz 3) como subárbol. El resultado es un árbol de orden 3.

La operación de fusión de dos montones se utiliza como subrutina en la mayoría de las demás operaciones. Una subrutina básica dentro de este procedimiento fusiona pares de árboles binomiales del mismo orden. Esto se puede hacer comparando las claves en las raíces de los dos árboles (las claves más pequeñas en ambos árboles). El nodo raíz con la clave más grande se convierte en un hijo del nodo raíz con la clave más pequeña, aumentando su orden en uno: ^{[1] [3]}

función mergeTree(p, q) si p.root.key <= q.root.key devuelve p.addSubTree(q) de lo contrario  devuelve q.addSubTree(p)

Esto muestra la fusión de dos montones binomiales. Esto se logra fusionando dos árboles binomiales del mismo orden uno por uno. Si el árbol fusionado resultante tiene el mismo orden que un árbol binomial en uno de los dos montones, entonces esos dos se fusionan nuevamente.

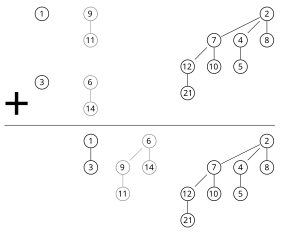
Para fusionar dos montones de manera más general, las listas de raíces de ambos montones se recorren simultáneamente de una manera similar a la del algoritmo de fusión , en una secuencia desde órdenes más pequeños de árboles a órdenes más grandes. Cuando solo uno de los dos montones que se fusionan contiene un árbol de orden , este árbol se mueve al montón de salida. Cuando ambos montones contienen un árbol de orden , los dos árboles se fusionan en un árbol de orden de modo que se cumpla la propiedad de montón mínimo. Más adelante puede ser necesario fusionar este árbol con algún otro árbol de orden en uno de los dos montones de entrada. En el transcurso del algoritmo, examinará como máximo tres árboles de cualquier orden, dos de los dos montones que fusionamos y uno compuesto por dos árboles más pequeños. ^{[1] [3]} ${\displaystyle j}$ ${\displaystyle j}$ ${\displaystyle j+1}$ ${\displaystyle j+1}$

función merge(p, q) mientras  no (p.end() y q.end()) árbol = mergeTree(p.currentTree(), q.currentTree())

 si  no es heap.currentTree().empty() árbol = mergeTree(árbol, montón.currentTree())

 montón.addTree(árbol) montón.siguiente(); p.siguiente(); q.siguiente()

Como cada árbol binomial en un montón binomial corresponde a un bit en la representación binaria de su tamaño, existe una analogía entre la fusión de dos montones y la suma binaria de los tamaños de los dos montones, de derecha a izquierda. Siempre que se produce un acarreo durante la suma, esto corresponde a una fusión de dos árboles binomiales durante la fusión. ^{[1] [3]}

El recorrido de cada árbol binomial durante la fusión solo involucra raíces, por lo que el tiempo empleado en la mayoría de los casos es de orden y, por lo tanto, el tiempo de ejecución es . ^{[1] [3]} ${\displaystyle \log _{2}n}$ ${\displaystyle O(\log n)}$

Insertar

La inserción de un nuevo elemento en un montón se puede realizar simplemente creando un nuevo montón que contenga solo este elemento y luego fusionándolo con el montón original. Debido a la fusión, una sola inserción lleva tiempo . Sin embargo, esto se puede acelerar utilizando un procedimiento de fusión que acorta la fusión después de que llega a un punto donde solo uno de los montones fusionados tiene árboles de orden mayor. Con esta aceleración, a lo largo de una serie de inserciones consecutivas, el tiempo total para las inserciones es . Otra forma de decirlo es que (después de la sobrecarga logarítmica para la primera inserción en una secuencia) cada inserción sucesiva tiene un tiempo amortizado de (es decir, constante) por inserción. ^{[1] [3]} ${\displaystyle O(\log n)}$ ${\displaystyle k}$ ${\displaystyle O(k+\log n)}$ ${\displaystyle O(1)}$

Una variante del montón binomial, el montón binomial sesgado , logra un tiempo de inserción constante en el peor de los casos mediante el uso de bosques cuyos tamaños de árboles se basan en el sistema numérico binario sesgado en lugar de en el sistema numérico binario. ^[4]

Encuentra el mínimo

Para encontrar el elemento mínimo del montón, hay que buscar el mínimo entre las raíces de los árboles binomiales. Esto se puede hacer a tiempo, ya que sólo hay raíces de árboles para examinar. ^[1] ${\displaystyle O(\log n)}$ ${\displaystyle O(\log n)}$

Al utilizar un puntero al árbol binomial que contiene el elemento mínimo, el tiempo para esta operación se puede reducir a . El puntero debe actualizarse al realizar cualquier operación que no sea la de encontrar el mínimo. Esto se puede hacer a tiempo por actualización, sin aumentar el tiempo de ejecución asintótico total de ninguna operación. ^{[ cita requerida ]} ${\displaystyle O(1)}$ ${\displaystyle O(\log n)}$

Eliminar mínimo

Para eliminar el elemento mínimo del montón, primero busque este elemento, quítelo de la raíz de su árbol binomial y obtenga una lista de sus subárboles hijos (que son cada uno de ellos árboles binomiales, de órdenes distintos). Transforme esta lista de subárboles en un montón binomial separado reordenándolos del orden más pequeño al más grande. Luego, fusione este montón con el montón original. Dado que cada raíz tiene como máximo hijos, crear este nuevo montón lleva tiempo . Fusionar montones lleva tiempo , por lo que toda la operación de eliminación del mínimo lleva tiempo . ^[1] ${\displaystyle \log _{2}n}$ ${\displaystyle O(\log n)}$ ${\displaystyle O(\log n)}$ ${\displaystyle O(\log n)}$

función deleteMin(montón) min = montón.árboles().primero() para cada corriente en heap.trees() si current.root < min.root entonces min = current para cada árbol en min.subTrees() tmp.addTree(árbol) montón.removeTree(min) fusionar(montón, temporal)

Tecla de disminución

Después de disminuir la clave de un elemento, puede llegar a ser más pequeña que la clave de su padre, violando la propiedad de montón mínimo. Si este es el caso, intercambie el elemento con su padre, y posiblemente también con su abuelo, y así sucesivamente, hasta que la propiedad de montón mínimo ya no se viole. Cada árbol binomial tiene una altura de como máximo , por lo que esto lleva tiempo. ^[1] Sin embargo, esta operación requiere que la representación del árbol incluya punteros desde cada nodo a su padre en el árbol, lo que complica un poco la implementación de otras operaciones. ^[3] ${\displaystyle \log _{2}n}$ ${\displaystyle O(\log n)}$

Borrar

Para eliminar un elemento del montón, disminuya su clave a infinito negativo (o equivalentemente, a un valor menor que cualquier elemento en el montón) y luego elimine el mínimo en el montón. ^[1]

Resumen de los tiempos de ejecución

Aquí se muestran las complejidades temporales ^[5] de varias estructuras de datos de montón. La abreviatura am. indica que la complejidad dada se amortiza, de lo contrario es una complejidad del peor caso. Para el significado de " O ( f )" y " Θ ( f )", consulte la notación Big O. Los nombres de las operaciones suponen un montón mínimo.

1. make-heap es la operación de construir un montón a partir de una secuencia de n elementos no ordenados. Se puede realizar en Θ ( n ) tiempo siempre que meld se ejecute en O (log  n ) tiempo (donde ambas complejidades se pueden amortizar). ^{[6] [7]} Otro algoritmo logra Θ ( n ) para montones binarios. ^[8]
2. Para los montículos persistentes (que no admiten decrease-key ), una transformación genérica reduce el costo de meld al de insert , mientras que el nuevo costo de delete-min es la suma de los costos anteriores de delete-min y meld . ^[11] Aquí, hace que meld se ejecute en Θ (1) tiempo (amortizado, si el costo de insert es) mientras que delete-min todavía se ejecuta en O (log  n ). Aplicado a montículos binomiales sesgados, produce colas Brodal-Okasaki, montículos persistentes con complejidades óptimas en el peor de los casos. ^[10]
3. Límite inferior de ^[14] límite superior de ^[15] ${\displaystyle \Omega (\log \log n),}$ ${\displaystyle O(2^{2{\sqrt {\log \log n}}}).}$
4. colas de Brodal y los montículos de Fibonacci estrictos logran complejidades óptimas en el peor de los casos para los montículos. Primero se describieron como estructuras de datos imperativas. La cola de Brodal-Okasaki es una estructura de datos persistente que logra el mismo óptimo, excepto que no se admite la clave de disminución .

Aplicaciones

• Simulación de eventos discretos
• Colas de prioridad

Véase también

• Montón débil , una combinación de las estructuras de datos del montón binario y del montón binomial

Referencias

1. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001) [1990]. "Capítulo 19: Binomial Heaps". Introducción a los algoritmos (2.ª ed.). MIT Press y McGraw-Hill. págs. 455–475. ISBN 0-262-03293-7.
2. Vuillemin, Jean (1 de abril de 1978). "Una estructura de datos para manipular colas de prioridad". Comunicaciones de la ACM . 21 (4): 309–315. doi : 10.1145/359460.359478 .
3. Brown, Mark R. (1978). "Implementación y análisis de algoritmos de cola binomial". Revista SIAM de Computación . 7 (3): 298–319. doi :10.1137/0207026. MR  0483830.
4. Brodal, Gerth Stølting; Okasaki, Chris (noviembre de 1996), "Colas de prioridad puramente funcionales óptimas", Journal of Functional Programming , 6 (6): 839–857, doi : 10.1017/s095679680000201x
5. Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L. (1990). Introducción a los algoritmos (1ª ed.). MIT Press y McGraw-Hill. ISBN 0-262-03141-8.
6. Sleator, Daniel Dominic ; Tarjan, Robert Endre (febrero de 1986). "Montones autoajustables". Revista SIAM de informática . 15 (1): 52–69. CiteSeerX 10.1.1.93.6678 . doi :10.1137/0215004. ISSN  0097-5397. 
7. Tarjan, Robert (1983). "3.3. Montones de izquierdas". Estructuras de datos y algoritmos de red . págs. 38-42. doi :10.1137/1.9781611970265. ISBN 978-0-89871-187-5.
8. Hayward, Ryan; McDiarmid, Colin (1991). "Análisis de caso promedio de construcción de montículos mediante inserción repetida" (PDF) . J. Algorithms . 12 : 126–153. CiteSeerX 10.1.1.353.7888 . doi :10.1016/0196-6774(91)90027-v. Archivado desde el original (PDF) el 5 de febrero de 2016 . Consultado el 28 de enero de 2016 . 
9. "Montón binomial | Wiki de matemáticas y ciencias brillante". brilliant.org . Consultado el 30 de septiembre de 2019 .
10. Brodal, Gerth Stølting; Okasaki, Chris (noviembre de 1996), "Colas de prioridad puramente funcionales óptimas", Journal of Functional Programming , 6 (6): 839–857, doi : 10.1017/s095679680000201x
11. Okasaki, Chris (1998). "10.2. Abstracción estructural". Estructuras de datos puramente funcionales (1.ª ed.). pp. 158-162. ISBN 9780521631242.
12. Takaoka, Tadao (1999), Teoría de 2-3 montones (PDF) , pág. 12
13. Iacono, John (2000), "Límites superiores mejorados para emparejar montones", Proc. 7th Scandinavian Workshop on Algorithm Theory (PDF) , Apuntes de clase en informática, vol. 1851, Springer-Verlag, págs. 63–77, arXiv : 1110.4428 , CiteSeerX 10.1.1.748.7812 , doi :10.1007/3-540-44985-X_5, ISBN  3-540-67690-2
14. Fredman, Michael Lawrence (julio de 1999). "Sobre la eficiencia de emparejar montones y estructuras de datos relacionadas" (PDF) . Revista de la Asociación de Maquinaria Computacional . 46 (4): 473–501. doi :10.1145/320211.320214.
15. Pettie, Seth (2005). Towards a Final Analysis of Pairing Heaps (PDF) . FOCS '05 Actas del 46.º Simposio anual IEEE sobre fundamentos de la informática. pp. 174–183. CiteSeerX 10.1.1.549.471 . doi :10.1109/SFCS.2005.75. ISBN .  0-7695-2468-0.
16. Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (noviembre de 2011). "Montones de emparejamiento de rangos" (PDF) . SIAM J. Informática . 40 (6): 1463–1485. doi :10.1137/100785351.
17. Fredman, Michael Lawrence ; Tarjan, Robert E. (julio de 1987). "Montones de Fibonacci y sus usos en algoritmos mejorados de optimización de redes" (PDF) . Revista de la Asociación de Maquinaria Computacional . 34 (3): 596–615. CiteSeerX 10.1.1.309.8927 . doi :10.1145/28869.28874. 
18. Brodal, Gerth Stølting ; Lagogiannis, George; Tarjan, Robert E. (2012). Montones de Fibonacci estrictos (PDF) . Actas del 44.º simposio sobre teoría de la computación - STOC '12. págs. 1177–1184. CiteSeerX 10.1.1.233.1740 . doi :10.1145/2213977.2214082. ISBN  978-1-4503-1245-5.
19. Brodal, Gerth S. (1996), "Colas de prioridad eficientes en el peor de los casos" (PDF) , Actas del 7.º Simposio anual ACM-SIAM sobre algoritmos discretos , págs. 52-58
20. Goodrich, Michael T .; Tamassia, Roberto (2004). "7.3.6. Construcción de montículos ascendentes". Estructuras de datos y algoritmos en Java (3.ª ed.). págs. 338–341. ISBN 0-471-46983-1.

Enlaces externos

• Dos implementaciones en C del montón binomial (una genérica y otra optimizada para claves enteras)
• Implementación de Haskell del montón binomial
• Implementación de montón binomial en Common Lisp