En matemáticas , un grupo alterno es el grupo de permutaciones pares de un conjunto finito . El grupo alterno en un conjunto de n elementos se llama grupo alterno de grado n , o grupo alterno en n letras y se denota por An o Alt( n ) .
Para n > 1 , el grupo An es el subgrupo del conmutador del grupo simétrico S n con índice 2 y por lo tanto tiene n ! /2 elementos. Es el núcleo del homomorfismo del grupo característico sgn: S n → {1, −1} explicado en el grupo simétrico .
El grupo An es abeliano si y sólo si n ≤ 3 y simple si y sólo si n = 3 o n ≥ 5 . Un 5 es el grupo simple no abeliano más pequeño , de orden 60, y el grupo más pequeño sin solución .
El grupo A 4 tiene los cuatro grupos V de Klein como un subgrupo normal propio , es decir, la identidad y las transposiciones dobles { (), (12)(34), (13)(24), (14)(23) } , ese es el núcleo de la sobreyección de A 4 sobre A 3 ≅ Z 3 . Tenemos la secuencia exacta V → A 4 → A 3 = Z 3 . En la teoría de Galois , esta aplicación, o más bien la aplicación correspondiente S 4 → S 3 , corresponde a asociar el resolutivo cúbico de Lagrange a un cuártico, lo que permite resolver el polinomio cuártico por radicales, tal como lo estableció Lodovico Ferrari .
Como en el grupo simétrico , dos elementos cualesquiera de An que estén conjugados por un elemento de An deben tener la misma forma de ciclo . Sin embargo, lo contrario no es necesariamente cierto. Si la forma del ciclo consta sólo de ciclos de longitud impar y no hay dos ciclos de la misma duración, donde los ciclos de longitud uno están incluidos en el tipo de ciclo, entonces hay exactamente dos clases de conjugación para esta forma de ciclo (Scott 1987, §11.1, p299 ).
Ejemplos:
Como los grupos simétricos finitos son los grupos de todas las permutaciones de un conjunto con elementos finitos, y los grupos alternos son grupos de permutaciones pares, los grupos alternos son subgrupos de grupos simétricos finitos.
Para n ≥ 3, An se genera mediante 3 ciclos, ya que se pueden obtener 3 ciclos combinando pares de transposiciones. Este conjunto generador se utiliza a menudo para demostrar que An es simple para n ≥ 5 .
Para n > 3 , excepto n = 6 , el grupo de automorfismo de An es el grupo simétrico S n , con un grupo de automorfismo interno An y un grupo de automorfismo externo Z 2 ; el automorfismo externo proviene de la conjugación mediante una permutación impar.
Para n = 1 y 2, el grupo de automorfismo es trivial. Para n = 3 el grupo de automorfismo es Z 2 , con un grupo de automorfismo interno trivial y un grupo de automorfismo externo Z 2 .
El grupo de automorfismo externo de A 6 es el grupo de cuatro grupos de Klein V = Z 2 × Z 2 , y está relacionado con el automorfismo externo de S 6 . El automorfismo externo adicional en A 6 intercambia los 3 ciclos (como (123)) con elementos de la forma 3 2 (como (123)(456) ).
Hay algunos isomorfismos excepcionales entre algunos de los pequeños grupos alternos y pequeños grupos de tipo Lie , particularmente grupos lineales especiales proyectivos . Estos son:
Más obviamente, A 3 es isomorfo al grupo cíclico Z 3 , y A 0 , A 1 y A 2 son isomorfos al grupo trivial (que también es SL 1 ( q ) = PSL 1 ( q ) para cualquier q ).


A 5 es el grupo de isometrías de un dodecaedro en el espacio tridimensional, por lo que existe una representación A 5 → SO 3 ( R ) .
En esta imagen los vértices de los poliedros representan los elementos del grupo, con el centro de la esfera representando el elemento de identidad. Cada vértice representa una rotación alrededor del eje que apunta desde el centro a ese vértice, por un ángulo igual a la distancia desde el origen, en radianes. Los vértices del mismo poliedro están en la misma clase de conjugación. Dado que la ecuación de clase de conjugación para A 5 es 1 + 12 + 12 + 15 + 20 = 60 , obtenemos cuatro poliedros distintos (no triviales).
Los vértices de cada poliedro están en correspondencia biyectiva con los elementos de su clase de conjugación, con la excepción de la clase de conjugación de (2,2)-ciclos, que está representada por un icosidodecaedro en la superficie exterior, con sus vértices antípodas identificados con entre sí. La razón de esta redundancia es que las rotaciones correspondientes son de π radianes y, por tanto, pueden representarse mediante un vector de longitud π en cualquiera de las dos direcciones. Así, la clase de (2,2) ciclos contiene 15 elementos, mientras que el icosidodecaedro tiene 30 vértices.
Las dos clases de conjugación de doce 5 ciclos en A 5 están representadas por dos icosaedros, de radios 2 π /5 y 4 π /5, respectivamente. El automorfismo externo no trivial en Out(A 5 ) ≃ Z 2 intercambia estas dos clases y los icosaedros correspondientes.
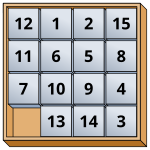
Se puede demostrar que el rompecabezas del 15 , un ejemplo famoso del rompecabezas deslizante , puede representarse mediante el grupo alterno A 15 , [2] porque las combinaciones del rompecabezas del 15 pueden generarse mediante 3 ciclos . De hecho, cualquier rompecabezas deslizante de 2 k − 1 con fichas cuadradas del mismo tamaño se puede representar mediante A 2 k −1 .
A 4 es el grupo más pequeño, lo que demuestra que lo inverso del teorema de Lagrange no es cierto en general: dado un grupo finito G y un divisor d de | G |, no existe necesariamente un subgrupo de G de orden d : el grupo G = A 4 , de orden 12, no tiene ningún subgrupo de orden 6. Un subgrupo de tres elementos (generado por una rotación cíclica de tres objetos) con cualquier elemento distinto y no trivial genera el grupo completo.
Para todo n > 4 , An no tiene subgrupos normales no triviales (es decir, propios) . Por tanto, An es un grupo simple para todo n > 4 . Un 5 es el grupo más pequeño que no tiene solución .
La homología de grupo de los grupos alternos muestra estabilización, como en la teoría de la homotopía estable : para n suficientemente grande , es constante. Sin embargo, existen algunas homologías excepcionales de baja dimensión. Tenga en cuenta que la homología del grupo simétrico exhibe una estabilización similar, pero sin las excepciones de baja dimensión (elementos de homología adicionales).
El primer grupo de homología coincide con la abelianización , y (dado que An es perfecto , salvo las excepciones citadas) es así:
Esto se ve fácilmente y directamente, de la siguiente manera. An es generado por 3 ciclos, por lo que los únicos mapas de abelianización no triviales son An → Z 3 , ya que los elementos de orden 3 deben asignarse a elementos de orden 3, y para n ≥ 5 todos los 3 ciclos son conjugados, por lo que deben asignarse al mismo elemento en la abelianización, ya que la conjugación es trivial en grupos abelianos. Por lo tanto, un ciclo de 3 como (123) debe asignarse al mismo elemento que su inverso (321), pero por lo tanto debe asignarse a la identidad, ya que debe tener un orden que divida 2 y 3, por lo que la abelianización es trivial.
Para n < 3 , An es trivial y, por tanto, tiene una abelianización trivial. Para A 3 y A 4 se puede calcular la abelianización directamente, observando que los 3 ciclos forman dos clases de conjugación (en lugar de que todas sean conjugadas) y que hay aplicaciones no triviales A 3 ↠ Z 3 (de hecho, un isomorfismo) y A 4 ↠ Z 3 .
Los multiplicadores de Schur de los grupos alternos An ( en el caso de que n sea al menos 5) son los grupos cíclicos de orden 2, excepto en el caso de que n sea 6 o 7, en cuyo caso también hay una triple cobertura. Entonces, en estos casos, el multiplicador de Schur es (el grupo cíclico) de orden 6. [3] Estos se calcularon por primera vez en (Schur 1911).
{{citation}}: CS1 maint: postscript (link)