
En teoría de grafos , un cactus (a veces llamado árbol de cactus ) es un grafo conexo en el que dos ciclos simples tienen como máximo un vértice en común. De manera equivalente, es un grafo conexo en el que cada arista pertenece como máximo a un ciclo simple, o (para cactus no triviales) en el que cada bloque (subgrafo máximo sin un vértice de corte ) es una arista o un ciclo.
Los cactus son grafos extraplanares . Cada pseudoárbol es un cactus. Un grafo no trivial es un cactus si y solo si cada bloque es un ciclo simple o una arista simple.
La familia de grafos en la que cada componente es un cactus está cerrada hacia abajo bajo las operaciones de grafos menores . Esta familia de grafos puede caracterizarse por un único grafo menor prohibido , el grafo de diamante de cuatro vértices formado al eliminar una arista del grafo completo K 4 . [1]
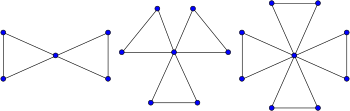
Un cactus triangular es un tipo especial de grafo de cactus, en el que cada ciclo tiene una longitud de tres y cada arista pertenece a un ciclo. Por ejemplo, los grafos de amistad , grafos formados a partir de una colección de triángulos unidos en un único vértice compartido, son cactus triangulares. Además de ser grafos de cactus, los cactus triangulares también son grafos de bloques y grafos localmente lineales .
Los cactus triangulares tienen la propiedad de permanecer conectados si se elimina cualquier coincidencia de ellos; para un número dado de vértices, tienen la menor cantidad posible de aristas con esta propiedad. Todo árbol con un número impar de vértices puede aumentarse a un cactus triangular añadiéndole aristas, lo que da como resultado un aumento mínimo con la propiedad de permanecer conectado después de la eliminación de una coincidencia. [2]
El cactus triangular más grande en cualquier grafo puede encontrarse en tiempo polinomial usando un algoritmo para el problema de paridad matroide . Dado que los grafos de cactus triangulares son grafos planares , el cactus triangular más grande puede usarse como una aproximación al subgrafo planar más grande, un subproblema importante en la planarización . Como algoritmo de aproximación , este método tiene una relación de aproximación de 4/9, la más conocida para el problema del subgrafo planar máximo. [3]
El algoritmo para encontrar el cactus triangular más grande está asociado con un teorema de Lovász y Plummer que caracteriza el número de triángulos en este cactus más grande. [4] Lovász y Plummer consideran pares de particiones de los vértices y aristas del grafo dado en subconjuntos, con la propiedad de que cada triángulo del grafo tiene dos vértices en una sola clase de la partición de vértices o las tres aristas en una sola clase de la partición de aristas; llaman a un par de particiones con esta propiedad válido . Entonces el número de triángulos en el cactus triangular más grande es igual al máximo, sobre pares de particiones válidas y , de
donde es el número de vértices en el gráfico dado y es el número de clases de vértice que cumple la clase de arista .
Cada grafo plano contiene un subgrafo de cactus que incluye al menos una fracción de las caras triangulares de . Este resultado implica un análisis directo del algoritmo de aproximación 4/9 para el problema del subgrafo plano máximo sin utilizar la fórmula min-max anterior. [5]
Una conjetura importante relacionada con el cactus triangular es la Conjetura de Rosa , llamada así por Alexander Rosa , que dice que todos los cactus triangulares son gráciles o casi gráciles. [6] Más precisamente
Todos los cactus triangulares con bloques t ≡ 0, 1 mod 4 son elegantes, y aquellos con t ≡ 2, 3 mod 4 son casi elegantes.
Algunos problemas de ubicación de instalaciones que son NP-difíciles para gráficos generales, así como algunos otros problemas de gráficos, se pueden resolver en tiempo polinomial para cactus. [7] [8]
Dado que los cactus son casos especiales de gráficos exteriores-planares , se pueden resolver varios problemas de optimización combinatoria en gráficos para ellos en tiempo polinomial . [9]
Los cactus representan circuitos eléctricos que tienen propiedades útiles. Una de las primeras aplicaciones de los cactus estuvo asociada con la representación de amplificadores operacionales. [10] [11] [12]
Los cactus también se han utilizado en genómica comparativa como una forma de representar la relación entre diferentes genomas o partes de genomas. [13]
Si un cactus está conectado, y cada uno de sus vértices pertenece a dos bloques como máximo, entonces se le llama cactus de Navidad . Todo grafo poliédrico tiene un subgrafo de cactus de Navidad que incluye todos sus vértices, un hecho que juega un papel esencial en una prueba de Leighton & Moitra (2010) de que todo grafo poliédrico tiene una incrustación voraz en el plano euclidiano , una asignación de coordenadas a los vértices para los cuales el reenvío voraz logra enrutar mensajes entre todos los pares de vértices. [14]
En la teoría de grafos topológicos , los grafos cuyas incrustaciones celulares son todas planares son exactamente la subfamilia de los grafos de cactus con la propiedad adicional de que cada vértice pertenece a un ciclo como máximo. Estos grafos tienen dos menores prohibidos, el grafo de diamante y el grafo de amistad de cinco vértices . [15]
Los cactus fueron estudiados por primera vez bajo el nombre de árboles Husimi , otorgado por Frank Harary y George Eugene Uhlenbeck en honor al trabajo previo sobre estos gráficos de Kôdi Husimi . [16] [17] El mismo artículo de Harary-Uhlenbeck reserva el nombre "cactus" para gráficos de este tipo en los que cada ciclo es un triángulo, pero ahora permitir ciclos de todas las longitudes es estándar.
Mientras tanto, el nombre de árbol de Husimi pasó a referirse comúnmente a los grafos en los que cada bloque es un grafo completo (equivalentemente, los grafos de intersección de los bloques en algún otro grafo). Este uso tenía poco que ver con el trabajo de Husimi, y ahora se utiliza el término más pertinente de grafo de bloques para esta familia; sin embargo, debido a esta ambigüedad, esta frase se ha vuelto menos utilizada para referirse a los grafos de cactus. [18]