
En geometría computacional , un diagrama de potencia , también llamado diagrama de Laguerre-Voronoi , complejo de celdas de Dirichlet , teselación radical de Voronoi o teselación seccional de Dirichlet , es una partición del plano euclidiano en celdas poligonales definidas a partir de un conjunto de círculos. La celda para un círculo dado C consiste en todos los puntos para los cuales la distancia de potencia a C es menor que la distancia de potencia a los otros círculos. El diagrama de potencia es una forma de diagrama de Voronoi generalizado y coincide con el diagrama de Voronoi de los centros de los círculos en el caso de que todos los círculos tengan radios iguales. [1] [2] [3] [4]

Si C es un círculo y P es un punto fuera de C , entonces la potencia de P con respecto a C es el cuadrado de la longitud de un segmento de línea desde P hasta un punto T de tangencia con C . De manera equivalente, si P tiene una distancia d desde el centro del círculo, y el círculo tiene un radio r , entonces (por el teorema de Pitágoras ) la potencia es d 2 − r 2 . La misma fórmula d 2 − r 2 puede extenderse a todos los puntos en el plano, independientemente de si están dentro o fuera de C : los puntos en C tienen potencia cero, y los puntos dentro de C tienen potencia negativa. [2] [3] [4]
El diagrama de potencia de un conjunto de n círculos C i es una partición del plano en n regiones R i (llamadas celdas), tales que un punto P pertenece a R i siempre que el círculo C i sea el círculo que minimiza la potencia de P . [2] [3] [4]
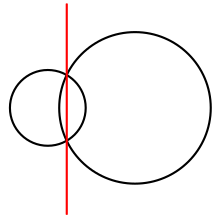
En el caso n = 2, el diagrama de potencias consta de dos semiplanos , separados por una línea llamada eje radical o cuerda de los dos círculos. A lo largo del eje radical, ambos círculos tienen la misma potencia. De manera más general, en cualquier diagrama de potencias, cada celda R i es un polígono convexo , la intersección de los semiespacios delimitados por los ejes radicales del círculo C i con cada uno de los otros círculos. Los triples de celdas se encuentran en los vértices del diagrama, que son los centros radicales de los tres círculos cuyas celdas se encuentran en el vértice. [2] [3] [4]
El diagrama de potencia puede verse como una forma ponderada del diagrama de Voronoi de un conjunto de puntos, una partición del plano en celdas dentro de las cuales uno de los puntos está más cerca que todos los demás. Otras formas de diagrama de Voronoi ponderado incluyen el diagrama de Voronoi ponderado aditivamente, en el que cada punto tiene un peso que se suma a su distancia antes de compararlo con las distancias a los otros puntos, y el diagrama de Voronoi ponderado multiplicativamente, en el que el peso de un punto se multiplica por su distancia antes de compararlo con las distancias a los otros puntos. En contraste, en el diagrama de potencia, podemos ver cada centro de círculo como un punto, y el radio al cuadrado de cada círculo como un peso que se resta de la distancia euclidiana al cuadrado antes de compararla con otras distancias al cuadrado. En el caso de que todos los radios de los círculos sean iguales, esta resta no hace ninguna diferencia en la comparación, y el diagrama de potencia coincide con el diagrama de Voronoi. [3] [4]
Un diagrama de potencia planar también puede interpretarse como una sección transversal planar de un diagrama de Voronoi tridimensional no ponderado. En esta interpretación, el conjunto de centros de círculos en el plano de la sección transversal son las proyecciones perpendiculares de los sitios de Voronoi tridimensionales, y el radio al cuadrado de cada círculo es una constante K menos la distancia al cuadrado del sitio correspondiente desde el plano de la sección transversal, donde K se elige lo suficientemente grande para hacer que todos estos radios sean positivos. [5]
Al igual que el diagrama de Voronoi, el diagrama de potencias puede generalizarse a espacios euclidianos de cualquier dimensión. El diagrama de potencias de n esferas en d dimensiones es combinatoriamente equivalente a la intersección de un conjunto de n semiespacios orientados hacia arriba en d + 1 dimensiones, y viceversa. [3]
Los diagramas de potencia bidimensionales pueden construirse mediante un algoritmo que se ejecuta en un tiempo O( n log n ). [2] [3] De manera más general, debido a la equivalencia con intersecciones de semiespacios de dimensiones superiores, los diagramas de potencia d -dimensionales (para d > 2) pueden construirse mediante un algoritmo que se ejecuta en un tiempo . [3]
El diagrama de potencias puede utilizarse como parte de un algoritmo eficiente para calcular el volumen de una unión de esferas. La intersección de cada esfera con su celda del diagrama de potencias proporciona su contribución a la unión total, a partir de la cual se puede calcular el volumen en un tiempo proporcional a la complejidad del diagrama de potencias. [6]
Otras aplicaciones de los diagramas de potencia incluyen estructuras de datos para probar si un punto pertenece a una unión de discos, [2] algoritmos para construir el límite de una unión de discos, [2] y algoritmos para encontrar las dos bolas más cercanas en un conjunto de bolas. [7] También se utiliza para resolver el problema de transporte óptimo semidiscreto [8] que a su vez tiene numerosas aplicaciones, como la reconstrucción del universo temprano [9] o la dinámica de fluidos. [10]
Aurenhammer (1987) rastrea la definición de la distancia de potencia al trabajo de los matemáticos del siglo XIX Edmond Laguerre y Georgy Voronoy . [3] Fejes Tóth (1977) definió los diagramas de potencia y los utilizó para demostrar que el límite de una unión de n discos circulares siempre puede iluminarse a partir de, como máximo, 2 n fuentes de luz puntuales. [11] Los diagramas de potencia han aparecido en la literatura con otros nombres, incluidos "diagrama de Laguerre-Voronoi", "complejo de células de Dirichlet", "teselación de Voronoi radical" y "teselación de Dirichlet seccional". [12]