
En la geometría neutra o absoluta , y en la geometría hiperbólica , puede haber muchas líneas paralelas a una línea dada que pasen por un punto que no esté en la línea ; sin embargo, en el plano, dos paralelas pueden estar más cerca que todas las demás (una en cada dirección de ).
Por lo tanto, es útil hacer una nueva definición sobre las paralelas en geometría neutra. Si hay paralelas más cercanas a una línea dada, se las conoce como paralelas límite , paralelas asintóticas u horoparalelas (horo del griego ὅριον - borde).
Para los rayos , la relación de paralelismo límite es una relación de equivalencia , que incluye la relación de equivalencia de ser coterminal.
Si en un triángulo hiperbólico los pares de lados son paralelos límites, entonces el triángulo es un triángulo ideal .
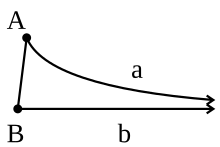
Un rayo es un paralelo límite a un rayo si son coterminales o si se encuentran en líneas distintas no iguales a la línea , no se encuentran y cada rayo en el interior del ángulo se encuentra con el rayo . [1]
Las líneas distintas que llevan rayos paralelos limitantes no se encuentran.
Supóngase que las líneas que llevan rayos paralelos distintos se encuentran. Por definición, no pueden encontrarse en el lado en el que se encuentra cualquiera de ellas . Entonces deben encontrarse en el lado opuesto a , llamemos a este punto . Por lo tanto . Contradicción.