En termodinámica de fluidos , la convección de Rayleigh-Bénard es un tipo de convección natural que ocurre en una capa horizontal plana de fluido calentado desde abajo, en la que el fluido desarrolla un patrón regular de celdas de convección conocidas como celdas de Bénard . Estos sistemas fueron investigados por primera vez por Joseph Valentin Boussinesq [1] y Anton Oberbeck [2] en el siglo XIX. Este fenómeno también puede manifestarse cuando una especie más densa que el electrolito se consume desde abajo y se genera en la parte superior. [3] La convección de Bénard-Rayleigh es uno de los fenómenos de convección más estudiados debido a su accesibilidad analítica y experimental. [4] Los patrones de convección son el ejemplo más cuidadosamente examinado de sistemas no lineales autoorganizados . [4] [5] Se conocen soluciones analíticas autosimilares dependientes del tiempo para los campos de velocidad y también para la distribución de temperatura. [6] [7]
La flotabilidad , y por lo tanto la gravedad , son responsables de la aparición de células de convección. El movimiento inicial es el afloramiento de fluido menos denso desde la capa inferior más cálida. [8] Este afloramiento se organiza espontáneamente en un patrón regular de células.

Las características de la convección de Bénard se pueden obtener mediante un experimento sencillo realizado por primera vez por Henri Bénard , un físico francés, en 1900.
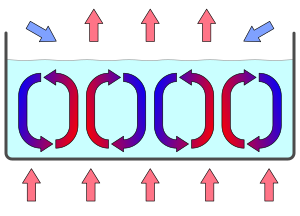
El experimento consiste en colocar una capa de líquido, por ejemplo agua, entre dos planos paralelos. La altura de la capa es pequeña en comparación con la dimensión horizontal. Al principio, la temperatura del plano inferior es la misma que la del plano superior. El líquido tenderá entonces hacia un equilibrio , en el que su temperatura será la misma que la del entorno. (Una vez allí, el líquido es perfectamente uniforme: para un observador parecería igual desde cualquier posición. Este equilibrio también es asintóticamente estable : después de una perturbación local y temporal de la temperatura exterior, volverá a su estado uniforme, de acuerdo con la segunda ley de la termodinámica ).
Luego, la temperatura del plano inferior aumenta ligeramente, lo que produce un flujo de energía térmica que se conduce a través del líquido. El sistema comenzará a tener una estructura de conductividad térmica : la temperatura, y con ella la densidad y la presión, variarán linealmente entre el plano inferior y el superior. Se establecerá un gradiente lineal uniforme de temperatura. (Este sistema puede modelarse mediante mecánica estadística ).
Una vez establecida la conducción, el movimiento aleatorio microscópico se ordena espontáneamente a nivel macroscópico, formando células de convección de Benard, con una longitud de correlación característica.

La rotación de las células es estable y alternará entre el sentido de las agujas del reloj y el sentido contrario a las agujas del reloj en sentido horizontal; este es un ejemplo de ruptura espontánea de la simetría . Las células de Bénard son metaestables . Esto significa que una pequeña perturbación no podrá cambiar la rotación de las células, pero una mayor podría afectar la rotación; exhiben una forma de histéresis .
Además, la ley determinista a nivel microscópico produce una disposición no determinista de las células: si se repite el experimento, una posición particular en el experimento será en una célula en el sentido de las agujas del reloj en algunos casos, y en una célula en el sentido contrario a las agujas del reloj en otros. Las perturbaciones microscópicas de las condiciones iniciales son suficientes para producir un efecto macroscópico no determinista. Es decir, en principio, no hay forma de calcular el efecto macroscópico de una perturbación microscópica. Esta incapacidad para predecir las condiciones a largo plazo y la sensibilidad a las condiciones iniciales son características de los sistemas caóticos o complejos (es decir, el efecto mariposa ).
Si se aumentara aún más la temperatura del plano inferior, la estructura se volvería más compleja en el espacio y en el tiempo; el flujo turbulento se volvería caótico .
Las células convectivas de Bénard tienden a aproximarse a prismas hexagonales rectos regulares, particularmente en ausencia de turbulencia, [10] [11] [12] aunque ciertas condiciones experimentales pueden resultar en la formación de prismas cuadrados rectos regulares [13] o espirales. [14]
Las celdas convectivas de Bénard no son únicas y normalmente aparecen solo en la convección impulsada por la tensión superficial. En general, las soluciones del análisis de Rayleigh y Pearson [15] (teoría lineal) que suponen una capa horizontal infinita dan lugar a una degeneración, lo que significa que el sistema puede obtener muchos patrones. Suponiendo una temperatura uniforme en las placas superior e inferior, cuando se utiliza un sistema realista (una capa con límites horizontales), la forma de los límites determinará el patrón. La mayoría de las veces, la convección aparecerá como rollos o una superposición de ellos.
Como existe un gradiente de densidad entre la placa superior y la inferior, la gravedad actúa intentando atraer el líquido más frío y denso desde la parte superior hacia la inferior. A esta fuerza gravitatoria se opone la fuerza de amortiguación viscosa del fluido. El equilibrio de estas dos fuerzas se expresa mediante un parámetro adimensional llamado número de Rayleigh . El número de Rayleigh se define como:
dónde
A medida que aumenta el número de Rayleigh, las fuerzas gravitacionales se vuelven más dominantes. En un número de Rayleigh crítico de 1708, [5] se produce inestabilidad y aparecen células de convección.
El número crítico de Rayleigh se puede obtener analíticamente para varias condiciones de contorno diferentes haciendo un análisis de perturbación sobre las ecuaciones linealizadas en el estado estable. [16] El caso más simple es el de dos contornos libres, que Lord Rayleigh resolvió en 1916, obteniendo Ra = 27 ⁄ 4 π 4 ≈ 657,51. [17] En el caso de un contorno rígido en la parte inferior y un contorno libre en la parte superior (como en el caso de una tetera sin tapa), el número crítico de Rayleigh resulta como Ra = 1.100,65. [18]
En el caso de una superficie líquida libre en contacto con el aire, los efectos de flotabilidad y tensión superficial también desempeñarán un papel en cómo se desarrollan los patrones de convección. Los líquidos fluyen desde lugares de menor tensión superficial a lugares de mayor tensión superficial. Esto se llama efecto Marangoni . Al aplicar calor desde abajo, la temperatura en la capa superior mostrará fluctuaciones de temperatura. Con el aumento de la temperatura, la tensión superficial disminuye. Por lo tanto, se producirá un flujo lateral de líquido en la superficie, [19] desde áreas más cálidas a áreas más frías. Para preservar una superficie de líquido horizontal (o casi horizontal), el líquido de la superficie más fría descenderá. Este descenso de líquido más frío contribuye a la fuerza impulsora de las celdas de convección. El caso específico de variaciones de tensión superficial impulsadas por gradientes de temperatura se conoce como convección termocapilar o convección de Bénard-Marangoni.
En 1870, el físico e ingeniero irlandés-escocés James Thomson (1822-1892), hermano mayor de Lord Kelvin , observó el enfriamiento del agua en una tina; notó que la película jabonosa en la superficie del agua estaba dividida como si la superficie hubiera sido embaldosada (teselada). En 1882, demostró que la teselación se debía a la presencia de celdas de convección. [20] En 1900, el físico francés Henri Bénard llegó de forma independiente a la misma conclusión. [21] Este patrón de convección, cuyos efectos se deben únicamente a un gradiente de temperatura, fue analizado con éxito por primera vez en 1916 por Lord Rayleigh . [22] Rayleigh asumió condiciones de contorno en las que el componente de velocidad vertical y la perturbación de la temperatura desaparecen en los límites superior e inferior (conducción térmica perfecta). Esas suposiciones dieron como resultado que el análisis perdiera cualquier conexión con el experimento de Henri Bénard. Esto dio lugar a discrepancias entre los resultados teóricos y experimentales hasta 1958, cuando John Pearson (1930– ) reelaboró el problema basándose en la tensión superficial. [15] Esto es lo que observó originalmente Bénard. No obstante, en el uso moderno, "convección de Rayleigh-Bénard" se refiere a los efectos debidos a la temperatura, mientras que "convección de Bénard-Marangoni" se refiere específicamente a los efectos de la tensión superficial. [4] Davis y Koschmieder han sugerido que la convección debería llamarse con razón "convección de Pearson-Bénard". [5]
La convección de Rayleigh-Bénard también se conoce a veces como "convección de Bénard-Rayleigh", "convección de Bénard" o "convección de Rayleigh".