Volatilidad (finanzas)

Grado de variación de una serie de precios comerciales a lo largo del tiempo

Índice de volatilidad CBOE (VIX) desde diciembre de 1985 hasta mayo de 2012 (cierres diarios)

En finanzas , la volatilidad (generalmente denotada por " σ ") es el grado de variación de una serie de precios comerciales a lo largo del tiempo, generalmente medida por la desviación estándar de los rendimientos logarítmicos .

La volatilidad histórica mide una serie temporal de precios de mercado pasados. La volatilidad implícita se proyecta hacia el futuro y se deriva del precio de mercado de un derivado comercializado en el mercado (en particular, una opción).

Terminología de volatilidad

La volatilidad tal como se describe aquí se refiere a la volatilidad real , más específicamente:

• volatilidad actual real de un instrumento financiero durante un período específico (por ejemplo, 30 días o 90 días), basada en precios históricos durante el período especificado, siendo la última observación el precio más reciente.
• volatilidad histórica real que se refiere a la volatilidad de un instrumento financiero durante un período específico pero con la última observación en una fecha en el pasado
  • Casi sinónimo es volatilidad realizada , la raíz cuadrada de la varianza realizada , a su vez calculada utilizando la suma de los rendimientos al cuadrado dividida por el número de observaciones.
• volatilidad futura real que se refiere a la volatilidad de un instrumento financiero durante un período específico que comienza en el momento actual y termina en una fecha futura (normalmente la fecha de vencimiento de una opción )

Pasando ahora a la volatilidad implícita , tenemos:

• volatilidad implícita histórica que se refiere a la volatilidad implícita observada a partir de los precios históricos del instrumento financiero (normalmente opciones)
• volatilidad implícita actual que se refiere a la volatilidad implícita observada a partir de los precios actuales del instrumento financiero
• volatilidad implícita futura que se refiere a la volatilidad implícita observada a partir de los precios futuros del instrumento financiero

En el caso de un instrumento financiero cuyo precio sigue un proceso aleatorio gaussiano o proceso de Wiener , el ancho de la distribución aumenta a medida que aumenta el tiempo. Esto se debe a que existe una probabilidad creciente de que el precio del instrumento se aleje más del precio inicial a medida que aumenta el tiempo. Sin embargo, en lugar de aumentar linealmente, la volatilidad aumenta con la raíz cuadrada del tiempo a medida que aumenta el tiempo, porque se espera que algunas fluctuaciones se cancelen entre sí, por lo que la desviación más probable después del doble de tiempo no será el doble de la distancia desde cero.

Dado que los cambios de precios observados no siguen distribuciones gaussianas, a menudo se utilizan otras distribuciones, como la de Lévy . ^[1] Estas pueden capturar atributos como las " colas gruesas ". La volatilidad es una medida estadística de dispersión en torno al promedio de cualquier variable aleatoria, como los parámetros del mercado, etc.

Definición matemática

Para cualquier fondo que evoluciona aleatoriamente con el tiempo, la volatilidad se define como la desviación estándar de una secuencia de variables aleatorias, cada una de las cuales es el rendimiento del fondo a lo largo de una secuencia correspondiente de tiempos (de igual tamaño).

Por lo tanto, la volatilidad "anualizada" σ _{anualmente es la desviación estándar de} los rendimientos logarítmicos anuales de un instrumento . ^[2]

La volatilidad generalizada σ _T para el horizonte temporal T en años se expresa como:

${\displaystyle \sigma _{\text{T}}=\sigma _{\text{annually}}{\sqrt {T}}.}$

Por lo tanto, si los rendimientos logarítmicos diarios de una acción tienen una desviación estándar de σ _diaria y el período de tiempo de los rendimientos es P en días de negociación, la volatilidad anualizada es

${\displaystyle \sigma _{\text{annually}}=\sigma _{\text{daily}}{\sqrt {P}}.}$

entonces

${\displaystyle \sigma _{\text{T}}=\sigma _{\text{daily}}{\sqrt {PT}}.}$

Una suposición común es que P = 252 días de negociación en un año determinado. Entonces, si σ _diaria = 0,01, la volatilidad anualizada es

${\displaystyle \sigma _{\text{annually}}=0.01{\sqrt {252}}=0.1587.}$

La volatilidad mensual (es decir, de un año) es ${\displaystyle T={\tfrac {1}{12}}}$

${\displaystyle \sigma _{\text{monthly}}=0.01{\sqrt {\tfrac {252}{12}}}=0.0458.}$

Las fórmulas utilizadas anteriormente para convertir los rendimientos o las medidas de volatilidad de un período de tiempo a otro suponen un modelo o proceso subyacente particular. Estas fórmulas son extrapolaciones precisas de un proceso aleatorio o proceso de Wiener, cuyos pasos tienen una varianza finita. Sin embargo, de manera más general, para los procesos estocásticos naturales, la relación precisa entre las medidas de volatilidad para diferentes períodos de tiempo es más complicada. Algunos utilizan el exponente de estabilidad de Lévy α para extrapolar los procesos naturales:

${\displaystyle \sigma _{T}=T^{1/\alpha }\sigma .\,}$

Si α = 2 se obtiene  la relación de escala del proceso de Wiener , pero algunas personas creen que α  < 2 para actividades financieras como acciones, índices, etc. Esto fue descubierto por Benoît Mandelbrot , quien analizó los precios del algodón y descubrió que seguían una distribución alfa-estable de Lévy con α  = 1,7. (Véase New Scientist, 19 de abril de 1997.)

Origen de la volatilidad

Se ha dedicado mucha investigación a modelar y pronosticar la volatilidad de los rendimientos financieros, y sin embargo pocos modelos teóricos explican cómo surge la volatilidad en primer lugar.

Roll (1984) muestra que la volatilidad se ve afectada por la microestructura del mercado . ^[3] Glosten y Milgrom (1985) muestran que al menos una fuente de volatilidad puede explicarse por el proceso de provisión de liquidez. Cuando los creadores de mercado infieren la posibilidad de una selección adversa , ajustan sus rangos de negociación, lo que a su vez aumenta la banda de oscilación de precios. ^[4]

En septiembre de 2019, JPMorgan Chase determinó el efecto de los tuits del presidente estadounidense Donald Trump y lo llamó el índice Volfefe que combina la volatilidad y el meme covfefe .

Volatilidad para los inversores

La volatilidad es importante para los inversores por al menos ocho razones, ^{[ cita requerida ]} varias de las cuales son afirmaciones alternativas de la misma característica o son directamente consecuentes entre sí:

1. Cuanto más amplias sean las oscilaciones del precio de una inversión, más difícil será emocionalmente no preocuparse;
2. La volatilidad del precio de un instrumento comercial puede ayudar a determinar el tamaño de la posición en una cartera;
3. Cuando se necesitan flujos de efectivo provenientes de la venta de un valor en una fecha futura específica para cumplir con un pasivo fijo conocido, una mayor volatilidad significa una mayor probabilidad de que se produzca un déficit;
4. Una mayor volatilidad de los rendimientos durante el ahorro para la jubilación da como resultado una distribución más amplia de los posibles valores finales de la cartera;
5. Una mayor volatilidad de los rendimientos después de la jubilación puede dar lugar a que los retiros tengan un impacto permanente mayor en el valor de la cartera;
6. La volatilidad de los precios presenta oportunidades para cualquiera que tenga información privilegiada para comprar activos a bajo precio y venderlos cuando están sobrevalorados;
7. La volatilidad afecta la fijación de precios de las opciones , siendo un parámetro del modelo Black-Scholes .

Volatilidad versus dirección

La volatilidad no mide la dirección de los cambios de precios, sino solo su dispersión. Esto se debe a que, al calcular la desviación estándar (o varianza ), se elevan al cuadrado todas las diferencias, de modo que las diferencias negativas y positivas se combinan en una sola cantidad. Dos instrumentos con diferentes volatilidades pueden tener el mismo rendimiento esperado, pero el instrumento con mayor volatilidad tendrá mayores oscilaciones en sus valores durante un período de tiempo determinado.

Por ejemplo, una acción con una volatilidad más baja puede tener una rentabilidad esperada (promedio) del 7%, con una volatilidad anual del 5%. Ignorando los efectos de capitalización, esto indicaría rentabilidades de aproximadamente -3% a +17% la mayor parte del tiempo (19 veces de cada 20, o 95% mediante una regla de dos desviaciones estándar). Una acción con una volatilidad más alta, con la misma rentabilidad esperada del 7% pero con una volatilidad anual del 20%, indicaría rentabilidades de aproximadamente -33% a +47% la mayor parte del tiempo (19 veces de cada 20, o 95%). Estas estimaciones suponen una distribución normal ; en realidad, se descubre que los movimientos de los precios de las acciones son leptocurtóticos (de cola gruesa).

Volatilidad a lo largo del tiempo

Aunque la ecuación de Black-Scholes supone una volatilidad constante predecible, esto no se observa en los mercados reales. Entre los modelos más realistas se encuentran el modelo de volatilidad local de Emanuel Derman e Iraj Kani ^[5] y el de Bruno Dupire , el proceso de Poisson en el que la volatilidad salta a nuevos niveles con una frecuencia predecible, y el cada vez más popular modelo de volatilidad estocástica de Heston ^[6] . [link roto]

Es de conocimiento común que muchos tipos de activos experimentan períodos de alta y baja volatilidad. Es decir, durante algunos períodos, los precios suben y bajan rápidamente, mientras que durante otros momentos apenas se mueven. ^[7] En el mercado de divisas , los cambios de precios son heterocedásticos estacionalmente con períodos de un día y una semana. ^{[8] [9]}

Los períodos en los que los precios caen rápidamente (un desplome ) suelen ir seguidos de una caída aún mayor o de una subida inusual. Asimismo, un período en el que los precios suben rápidamente (una posible burbuja ) puede ir seguido de una subida aún mayor o de una bajada inusual.

Lo más habitual es que los movimientos extremos no aparezcan "de la nada", sino que estén presagiados por movimientos mayores de lo habitual o por la incertidumbre conocida sobre acontecimientos futuros específicos. Esto se denomina heterocedasticidad condicional autorregresiva . Es más difícil decir si esos grandes movimientos tienen la misma dirección o la opuesta. Y un aumento de la volatilidad no siempre presagia un aumento mayor: la volatilidad puede simplemente volver a bajar.

Las medidas de volatilidad dependen no sólo del período en el que se miden, sino también de la resolución temporal seleccionada, ya que el flujo de información entre los traders de corto y largo plazo es asimétrico. ^{[ aclaración necesaria ]} Como resultado, la volatilidad medida con alta resolución contiene información que no está cubierta por la volatilidad de baja resolución y viceversa. ^[10]

La volatilidad ponderada por paridad de riesgo de los tres activos, oro, bonos del Tesoro y Nasdaq, que actúa como proxy de Marketportfolio ^{[ aclaración necesaria ],} parece haber alcanzado un mínimo del 4% después de haber subido por octava vez desde 1974 en esta lectura en el verano de 2014. ^{[ aclaración necesaria ] [ cita necesaria ]}

Medidas alternativas de volatilidad

Algunos autores señalan que la volatilidad realizada y la volatilidad implícita son medidas retrospectivas y prospectivas, y no reflejan la volatilidad actual. Para abordar esa cuestión, se sugirió una alternativa: las medidas de volatilidad por conjuntos. Una de las medidas se define como la desviación estándar de los rendimientos por conjuntos en lugar de series temporales de rendimientos. ^[11] Otra considera la secuencia regular de cambios direccionales como el indicador de la volatilidad instantánea. ^[12]

La volatilidad en relación con el trading de opciones

Un método para medir la volatilidad, que suelen utilizar las empresas de operaciones cuantitativas con opciones, divide la volatilidad en dos componentes: la volatilidad limpia (la cantidad de volatilidad causada por eventos estándar, como transacciones diarias y ruido general) y la volatilidad sucia (la cantidad causada por eventos específicos, como los anuncios de ganancias o políticas). ^[13] Por ejemplo, una empresa como Microsoft tendría una volatilidad limpia causada por personas que compran y venden a diario, pero una volatilidad sucia (o volatilidad de eventos) por ejemplo, por ganancias trimestrales o un posible anuncio antimonopolio.

Desglosar la volatilidad en dos componentes es útil para calcular con precisión el valor de una opción, especialmente para identificar qué eventos pueden contribuir a una oscilación. El trabajo de los analistas fundamentales en los creadores de mercado y las empresas boutique de negociación de opciones generalmente implica intentar asignar valores numéricos a estos números.

Parametrización de la volatilidad implícita

Existen varias parametrizaciones conocidas de la superficie de volatilidad implícita: Schonbucher, SVI y gSVI. ^[14]

Estimación de la volatilidad del crudo

Si se simplifica la fórmula anterior, es posible estimar la volatilidad anualizada basándose únicamente en observaciones aproximadas. Supongamos que se observa que un índice de precios de mercado, cuyo valor actual se acerca a 10 000, se ha movido unos 100 puntos al día, en promedio, durante muchos días. Esto constituiría un movimiento diario del 1 %, hacia arriba o hacia abajo.

Para anualizar esto, se puede utilizar la "regla del 16", es decir, multiplicar por 16 para obtener el 16% como volatilidad anual. La razón de esto es que 16 es la raíz cuadrada de 256, que es aproximadamente el número de días de negociación en un año (252). Esto también utiliza el hecho de que la desviación estándar de la suma de n variables independientes (con desviaciones estándar iguales) es √n veces la desviación estándar de las variables individuales.

Sin embargo, lo más importante es que esto no captura (o en algunos casos puede dar un peso excesivo a) los grandes movimientos ocasionales en el precio del mercado que ocurren con menos frecuencia que una vez al año.

La magnitud promedio de las observaciones es simplemente una aproximación de la desviación estándar del índice de mercado. Suponiendo que los cambios diarios del índice de mercado se distribuyen normalmente con media cero y desviación estándar  σ , el valor esperado de la magnitud de las observaciones es √(2/ π ) σ = 0,798 σ . El efecto neto es que este enfoque burdo subestima la volatilidad real en aproximadamente un 20%.

Estimación de la tasa de crecimiento anual compuesta (CAGR)

Consideremos la serie de Taylor :

${\displaystyle \log(1+y)=y-{\tfrac {1}{2}}y^{2}+{\tfrac {1}{3}}y^{3}-{\tfrac {1}{4}}y^{4}+\cdots }$

Tomando sólo los dos primeros términos se tiene:

${\displaystyle \mathrm {CAGR} \approx \mathrm {AR} -{\tfrac {1}{2}}\sigma ^{2}}$

Por lo tanto, la volatilidad representa matemáticamente un lastre para la CAGR (formalizada como el " impuesto a la volatilidad "). En términos realistas, la mayoría de los activos financieros tienen asimetría negativa y leptocurtosis, por lo que esta fórmula tiende a ser demasiado optimista. Algunas personas utilizan la fórmula:

${\displaystyle \mathrm {CAGR} \approx \mathrm {AR} -{\tfrac {1}{2}}k\sigma ^{2}}$

Para una estimación aproximada, donde k es un factor empírico (normalmente de cinco a diez). ^{[ cita requerida ]}

Críticas a los modelos de previsión de volatilidad

Rendimiento del VIX (izquierda) comparado con la volatilidad pasada (derecha) como predictores de volatilidad de 30 días, para el período de enero de 1990 a septiembre de 2009. La volatilidad se mide como la desviación estándar de los retornos de un día del S&P500 durante un período de un mes. Las líneas azules indican regresiones lineales , lo que da como resultado los coeficientes de correlación r que se muestran. Nótese que el VIX tiene virtualmente el mismo poder predictivo que la volatilidad pasada, en la medida en que los coeficientes de correlación mostrados son casi idénticos.

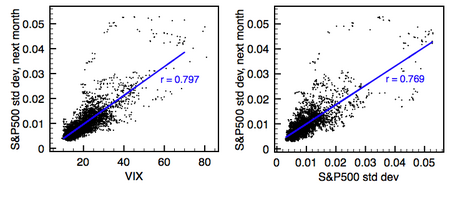
A pesar de la sofisticada composición de la mayoría de los modelos de predicción de la volatilidad, los críticos afirman que su poder predictivo es similar al de las medidas tradicionales, como la simple volatilidad pasada ^{[15] [16],} especialmente fuera de la muestra, donde se utilizan diferentes datos para estimar los modelos y probarlos. ^[17] Otros trabajos han estado de acuerdo, pero afirman que los críticos no implementaron correctamente los modelos más complicados. ^[18] Algunos profesionales y administradores de cartera parecen ignorar o descartar por completo los modelos de predicción de la volatilidad. Por ejemplo, Nassim Taleb tituló famosamente uno de sus artículos en Journal of Portfolio Management "No sabemos exactamente de qué estamos hablando cuando hablamos de volatilidad". ^[19] En una nota similar, Emanuel Derman expresó su desilusión con la enorme oferta de modelos empíricos no respaldados por la teoría. ^[20] Sostiene que, si bien "las teorías son intentos de descubrir los principios ocultos que sustentan el mundo que nos rodea, como lo hizo Albert Einstein con su teoría de la relatividad", debemos recordar que "los modelos son metáforas: analogías que describen una cosa en relación con otra".

Véase también

• Beta (finanzas)  : cambio esperado en el precio de una acción en relación con todo el mercado
• Dispersión  : propiedad estadística que cuantifica en qué medida se dispersa una colección de datos.
• Economía financiera  – Disciplina académica que se ocupa del intercambio de dinero.
• IVX  : índice de volatilidad intradía similar al VIX para valores estadounidenses e instrumentos cotizados en bolsa
• Jules Regnault  – economista francésPáginas que muestran descripciones de wikidata como alternativa
• Riesgo  – Posibilidad de que algo malo suceda
• VIX  – Índice de volatilidad
• Sonrisa de volatilidad  : patrones de volatilidad implícitos que surgen al fijar el precio de las opciones financieras
• Impuesto a la volatilidad  : término matemático financiero
• Riesgo de volatilidad
• Volatilidad beta

Referencias

1. "Distribución de impuestos". wilmottwiki.com .
2. "Cálculo de la volatilidad histórica: ejemplo paso a paso" (PDF) . Archivado desde el original el 30 de marzo de 2012. Consultado el 18 de agosto de 2011 .{{cite web}}: CS1 maint: bot: estado de URL original desconocido ( enlace )
3. Roll, R. (1984): "Una medida implícita simple del diferencial efectivo entre oferta y demanda en un mercado eficiente", Journal of Finance 39 (4), 1127–1139
4. Glosten, LR y PR Milgrom (1985): "Precios de oferta, demanda y transacción en un mercado especializado con operadores informados heterogéneamente", Journal of Financial Economics 14 (1), 71–100
5. Derman, E., Iraj Kani (1994). ""Riding on a Smile". RISK, 7(2) Feb.1994, pp. 139–145, pp. 32–39" (PDF) . Risk. Archivado desde el original (PDF) el 10 de julio de 2011 . Consultado el 1 de junio de 2007 . {{cite journal}}: Requiere citar revista |journal=( ayuda )Mantenimiento de CS1: varios nombres: lista de autores ( enlace )
6. "Volatilidad". wilmottwiki.com .
7. "Cómo aprovechar los picos de volatilidad con los diferenciales de crédito".
8. Müller, Ulrich A.; Dacorogna, Michel M.; Olsen, Richard B.; Pictet, Olivier V.; Schwarz, Matthias; Morgenegg, Claude (1 de diciembre de 1990). "Estudio estadístico de los tipos de cambio, evidencia empírica de una ley de escala de cambio de precios y análisis intradiario". Journal of Banking & Finance . 14 (6): 1189–1208. doi :10.1016/0378-4266(90)90009-Q. ISSN  0378-4266.
9. Petrov, Vladimir; Golub, Anton; Olsen, Richard (junio de 2019). "Estacionalidad de la volatilidad instantánea de los mercados de alta frecuencia en el tiempo intrínseco de cambio direccional". Journal of Risk and Financial Management . 12 (2): 54. doi : 10.3390/jrfm12020054 . hdl : 10419/239003 .
10. Muller, Ulrich A.; Dacorogna, Michel; Dave, Rakhal D.; Olsen, Richard; Pictet, Olivier V.; von Weizsäcker, Jakob (1997). "Volatilidades de diferentes resoluciones temporales: análisis de la dinámica de los componentes del mercado". Journal of Empirical Finance . 4 (2–3): 213–239. doi :10.1016/S0927-5398(97)00007-8. ISSN  0927-5398.
11. Sarkissian, Jack (2016). "Medición expresa de la volatilidad del mercado mediante el concepto de ergodicidad". doi :10.2139/ssrn.2812353. S2CID  168496910. SSRN  2812353. {{cite journal}}: Requiere citar revista |journal=( ayuda )
12. Petrov, Vladimir; Golub, Anton; Olsen, Richard (junio de 2019). "Estacionalidad de la volatilidad instantánea de los mercados de alta frecuencia en el tiempo intrínseco de cambio direccional". Journal of Risk and Financial Management . 12 (2): 54. doi : 10.3390/jrfm12020054 . hdl : 10419/239003 .
13. "Limpieza de volúmenes implícitos". Moontowermeta . Consultado el 26 de junio de 2024 .
14. Babak Mahdavi Damghani y Andrew Kos (2013). "Desarbitrar con una sonrisa débil". Wilmott. {{cite journal}}: Requiere citar revista |journal=( ayuda ) http://www.readcube.com/articles/10.1002/wilm.10201?locale=en
15. Cumby, R.; Figlewski, S.; Hasbrouck, J. (1993). "Pronóstico de volatilidad y correlaciones con modelos EGARCH". Journal of Derivatives . 1 (2): 51–63. doi :10.3905/jod.1993.407877. S2CID  154028452.
16. Jorion, P. (1995). "Predicción de la volatilidad en el mercado de divisas". Journal of Finance . 50 (2): 507–528. doi :10.1111/j.1540-6261.1995.tb04793.x. JSTOR  2329417.
17. Brooks, Chris ; Persand, Gita (2003). "Previsión de volatilidad para la gestión de riesgos". Journal of Forecasting . 22 (1): 1–22. CiteSeerX 10.1.1.595.9113 . doi :10.1002/for.841. ISSN  1099-131X. S2CID  154615850. 
18. Andersen, Torben G.; Bollerslev, Tim (1998). "Respondiendo a los escépticos: sí, los modelos de volatilidad estándar sí proporcionan pronósticos precisos". International Economic Review . 39 (4): 885–905. CiteSeerX 10.1.1.28.454 . doi :10.2307/2527343. JSTOR  2527343. 
19. Goldstein, Daniel y Taleb, Nassim, (28 de marzo de 2007) "No sabemos exactamente de qué estamos hablando cuando hablamos de volatilidad". Journal of Portfolio Management 33 (4), 2007.
20. Derman, Emanuel (2011): Modelos que se comportan mal: por qué confundir la ilusión con la realidad puede conducir al desastre, en Wall Street y en la vida”, Ed. Free Press.

Enlaces externos

• Comparación gráfica de la volatilidad implícita e histórica ^{[ vínculo muerto permanente ]} , video
• Diebold, Francis X.; Hickman, Andrew; Inoue, Atsushi y Schuermann, Til (1996) "Convertir la volatilidad de un día a la volatilidad de un día: escalar por sqrt(h) es peor de lo que se piensa"
• Una breve introducción a los conceptos matemáticos alternativos de volatilidad
• Estimación de la volatilidad a partir de la densidad de retorno prevista Ejemplo basado en la distribución de retorno diario de Google utilizando la función de densidad estándar
• Documento de investigación que incluye un extracto del informe titulado Identificación de volatilidad rica y barata Extracto de Enhanced Call Overwriting, un informe de Ryan Renicker y Devapriya Mallick en Lehman Brothers (2005).

Lectura adicional

• Bartram, Söhnke M.; Brown, Gregory W.; Stulz, Rene M. (agosto de 2012). "¿Por qué las acciones estadounidenses son más volátiles?" (PDF) . Journal of Finance . 67 (4): 1329–1370. doi :10.1111/j.1540-6261.2012.01749.x. S2CID  18587238. SSRN  2257549.
• Natenberg, Sheldon (2015). Volatilidad y fijación de precios de opciones: estrategias y técnicas de negociación avanzadas (segunda edición). Nueva York. ISBN 978-0071818773.{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace )