En informática , la transformación de gráficos o reescritura de gráficos se refiere a la técnica de crear un nuevo gráfico a partir de un gráfico original de forma algorítmica. Tiene numerosas aplicaciones, que van desde la ingeniería de software ( construcción de software y también verificación de software ) hasta algoritmos de diseño y generación de imágenes.
Las transformaciones de grafos se pueden utilizar como una abstracción computacional. La idea básica es que si el estado de un cómputo se puede representar como un grafo, los pasos posteriores de ese cómputo se pueden representar como reglas de transformación en ese grafo. Dichas reglas consisten en un grafo original, que se debe hacer coincidir con un subgrafo en el estado completo, y un grafo de reemplazo, que reemplazará al subgrafo coincidente.
Formalmente, un sistema de reescritura de grafos suele constar de un conjunto de reglas de reescritura de grafos de la forma , siendo llamado grafo de patrón (o lado izquierdo) y siendo llamado grafo de reemplazo (o lado derecho de la regla). Una regla de reescritura de grafos se aplica al grafo anfitrión buscando una ocurrencia del grafo de patrón ( coincidencia de patrones , resolviendo así el problema de isomorfismo de subgrafos ) y reemplazando la ocurrencia encontrada por una instancia del grafo de reemplazo. Las reglas de reescritura se pueden regular aún más en el caso de grafos etiquetados , como en las gramáticas de grafos reguladas por cadenas.
A veces, la gramática de gráficos se utiliza como sinónimo de sistema de reescritura de gráficos , especialmente en el contexto de lenguajes formales ; la redacción diferente se utiliza para enfatizar el objetivo de las construcciones, como la enumeración de todos los gráficos a partir de un gráfico inicial, es decir, la generación de un lenguaje de gráficos, en lugar de simplemente transformar un estado dado (gráfico anfitrión) en un nuevo estado.
El enfoque algebraico para la reescritura de grafos se basa en la teoría de categorías . El enfoque algebraico se divide a su vez en subenfoques, los más comunes de los cuales son el enfoque de doble empuje (DPO) y el enfoque de empuje simple (SPO) . Otros subenfoques incluyen el enfoque de sesqui-pushout y el enfoque de pullback .
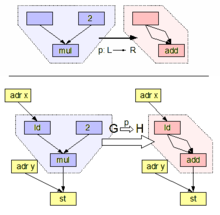
Desde la perspectiva del enfoque DPO, una regla de reescritura de grafos es un par de morfismos en la categoría de grafos y homomorfismos de grafos entre ellos: , también escrito , donde es inyectivo . El grafo K se llama invariante o, a veces, grafo de unión . Un paso de reescritura o aplicación de una regla r a un grafo anfitrión G se define por dos diagramas de expulsión , ambos originados en el mismo morfismo , donde D es un grafo de contexto (de aquí proviene el nombre de doble expulsión). Otro morfismo de grafo modela una ocurrencia de L en G y se llama coincidencia . La comprensión práctica de esto es que es un subgrafo que se empareja desde (ver problema de isomorfismo de subgrafo ), y después de que se encuentra una coincidencia, se reemplaza con en el grafo anfitrión donde sirve como una interfaz, que contiene los nodos y los bordes que se conservan al aplicar la regla. El grafo es necesario para adjuntar el patrón que se está emparejando a su contexto: si está vacío, la coincidencia solo puede designar un componente conectado completo del grafo .
En contraste, una regla de reescritura de grafos del enfoque SPO es un único morfismo en la categoría de multigrafos etiquetados y mapeos parciales que preservan la estructura del multigrafo: . Por lo tanto, un paso de reescritura se define mediante un único diagrama de expulsión . La comprensión práctica de esto es similar al enfoque DPO. La diferencia es que no hay una interfaz entre el grafo anfitrión G y el grafo G' que es el resultado del paso de reescritura.
Desde una perspectiva práctica, la distinción clave entre DPO y SPO es cómo tratan la eliminación de nodos con aristas adyacentes, en particular, cómo evitan que dichas eliminaciones puedan dejar "aristas colgantes". El enfoque DPO solo elimina un nodo cuando la regla especifica también la eliminación de todas las aristas adyacentes (esta condición de aristas colgantes se puede comprobar para una coincidencia determinada), mientras que el enfoque SPO simplemente elimina las aristas adyacentes, sin requerir una especificación explícita.
Existe también otro enfoque de tipo algebraico para la reescritura de gráficos, basado principalmente en el álgebra de Boole y un álgebra de matrices, llamadas gramáticas de gráficos matriciales . [1]
Otro enfoque para la reescritura de gráficos, conocido como reescritura de gráficos determinada , surgió de la lógica y la teoría de bases de datos . [2] En este enfoque, los gráficos se tratan como instancias de bases de datos y las operaciones de reescritura como un mecanismo para definir consultas y vistas; por lo tanto, se requiere que toda reescritura produzca resultados únicos ( hasta el isomorfismo ), y esto se logra aplicando cualquier regla de reescritura simultáneamente en todo el gráfico, donde sea que se aplique, de tal manera que el resultado esté realmente definido de manera única.
Otro enfoque para la reescritura de gráficos es la reescritura de gráficos de términos , que implica el procesamiento o la transformación de gráficos de términos (también conocidos como gráficos semánticos abstractos ) mediante un conjunto de reglas de reescritura sintáctica.
Los gráficos de términos son un tema destacado en la investigación de lenguajes de programación, ya que las reglas de reescritura de gráficos de términos son capaces de expresar formalmente la semántica operacional de un compilador . Los gráficos de términos también se utilizan como máquinas abstractas capaces de modelar cálculos químicos y biológicos, así como cálculos gráficos como los modelos de concurrencia. Los gráficos de términos pueden realizar verificación automatizada y programación lógica, ya que son adecuados para representar declaraciones cuantificadas en lógica de primer orden. El software de programación simbólica es otra aplicación para los gráficos de términos, que son capaces de representar y realizar cálculos con estructuras algebraicas abstractas como grupos, campos y anillos.
La conferencia TERMGRAPH [3] se centra enteramente en la investigación sobre la reescritura de gráficos de términos y sus aplicaciones.
Los sistemas de reescritura de grafos se agrupan naturalmente en clases según el tipo de representación de grafos que se utilizan y cómo se expresan las reescrituras. El término gramática de grafos, que también es equivalente a sistema de reescritura de grafos o sistema de reemplazo de grafos, se utiliza con más frecuencia en las clasificaciones. Algunos tipos comunes son:
Los grafos son un formalismo expresivo, visual y matemáticamente preciso para modelar objetos (entidades) vinculados por relaciones; los objetos se representan mediante nodos y las relaciones entre ellos mediante aristas. Los nodos y las aristas suelen estar tipificados y atribuidos. Los cálculos se describen en este modelo mediante cambios en las relaciones entre las entidades o mediante cambios de atributos de los elementos del grafo. Se codifican en reglas de reescritura/transformación de grafos y se ejecutan mediante sistemas de reescritura/herramientas de transformación de grafos.