
El término estructura magnética de un material se refiere a la disposición ordenada de los espines magnéticos, normalmente dentro de una red cristalográfica ordenada . Su estudio es una rama de la física del estado sólido .
La mayoría de los materiales sólidos no son magnéticos, es decir, no presentan una estructura magnética. Debido al principio de exclusión de Pauli , cada estado está ocupado por electrones de espines opuestos, de modo que la densidad de carga se compensa en todas partes y el grado de libertad de espín es insignificante. Aun así, estos materiales suelen mostrar un comportamiento magnético débil, por ejemplo, debido al diamagnetismo o al paramagnetismo de Pauli .
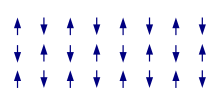
El caso más interesante es cuando el electrón del material rompe espontáneamente la simetría mencionada anteriormente. Para el ferromagnetismo en el estado fundamental, existe un eje de cuantificación de espín común y un exceso global de electrones de un número cuántico de espín dado, hay más electrones apuntando en una dirección que en la otra, dando una magnetización macroscópica (típicamente, la mayoría de los electrones se eligen para apuntar hacia arriba). En los casos más simples (colineales) de antiferromagnetismo , todavía existe un eje de cuantificación común, pero los espines electrónicos apuntan alternativamente hacia arriba y hacia abajo, lo que conduce nuevamente a la cancelación de la magnetización macroscópica. Sin embargo, específicamente en el caso de frustración de las interacciones, las estructuras resultantes pueden volverse mucho más complicadas, con orientaciones inherentemente tridimensionales de los espines locales. Finalmente, el ferromagnetismo , tal como se muestra prototípicamente por la magnetita, es en cierto sentido un caso intermedio: aquí la magnetización no está compensada globalmente como en el ferromagnetismo, pero la magnetización local apunta en diferentes direcciones.
La discusión anterior se refiere a la estructura del estado fundamental. Por supuesto, las temperaturas finitas conducen a excitaciones de la configuración de espín. Aquí se pueden contrastar dos puntos de vista extremos: en la imagen de Stoner del magnetismo (también llamado magnetismo itinerante), los estados electrónicos están deslocalizados y su interacción de campo medio conduce a la ruptura de la simetría. En esta visión, con el aumento de la temperatura, la magnetización local disminuiría de manera homogénea, ya que los electrones deslocalizados individuales se mueven del canal ascendente al descendente. Por otro lado, en el caso del momento local, los estados electrónicos están localizados en átomos específicos, lo que da lugar a espines atómicos que interactúan solo en un rango corto y, por lo general, se analizan con el modelo de Heisenberg . Aquí, las temperaturas finitas conducen a una desviación de las orientaciones de los espines atómicos con respecto a la configuración ideal, por lo que para un ferroimán también disminuye la magnetización macroscópica.
En el caso del magnetismo localizado, muchas estructuras magnéticas pueden describirse mediante grupos espaciales magnéticos , que dan cuenta con precisión de todos los grupos de simetría posibles de configuraciones arriba/abajo en un cristal tridimensional. Sin embargo, este formalismo no puede dar cuenta de algunas estructuras magnéticas más complejas, como las que se encuentran en el helimagnetismo .
Este ordenamiento se puede estudiar observando la susceptibilidad magnética en función de la temperatura y/o del tamaño del campo magnético aplicado, pero una imagen verdaderamente tridimensional de la disposición de los espines se obtiene mejor por medio de la difracción de neutrones . [1] [2] Los neutrones se dispersan principalmente por los núcleos de los átomos en la estructura. A una temperatura por encima del punto de ordenamiento de los momentos magnéticos, donde el material se comporta como uno paramagnético, la difracción de neutrones dará por lo tanto una imagen de la estructura cristalográfica solamente. Por debajo del punto de ordenamiento, por ejemplo la temperatura de Néel de un antiferroimán o el punto de Curie de un ferroimán, los neutrones también experimentarán dispersión de los momentos magnéticos porque ellos mismos poseen espín. Por lo tanto, las intensidades de las reflexiones de Bragg cambiarán. De hecho, en algunos casos se producirán reflexiones de Bragg completamente nuevas si la celda unitaria del ordenamiento es mayor que la de la estructura cristalográfica. Esta es una forma de formación de superestructura . Por lo tanto, la simetría de la estructura total puede diferir de la subestructura cristalográfica. Debe describirse mediante uno de los 1651 grupos magnéticos ( Shubnikov ) en lugar de uno de los grupos espaciales no magnéticos . [3]
Aunque la difracción de rayos X ordinaria es "ciega" a la disposición de los espines, se ha hecho posible utilizar una forma especial de difracción de rayos X para estudiar la estructura magnética. Si se selecciona una longitud de onda cercana a un borde de absorción de uno de los elementos contenidos en los materiales, la dispersión se vuelve anómala y este componente de la dispersión es (en cierta medida) sensible a la forma no esférica de los electrones externos de un átomo con un espín desapareado. Esto significa que este tipo de difracción de rayos X anómala contiene información del tipo deseado.
Más recientemente, se están desarrollando técnicas de sobremesa que permiten estudiar estructuras magnéticas sin recurrir a fuentes de neutrones o sincrotrón. [4]
Solo tres elementos son ferromagnéticos a temperatura y presión ambiente: hierro , cobalto y níquel . Esto se debe a que su temperatura de Curie , Tc , es más alta que la temperatura ambiente ( Tc > 298 K ). El gadolinio tiene una magnetización espontánea justo por debajo de la temperatura ambiente (293 K) y a veces se lo considera el cuarto elemento ferromagnético. Se ha sugerido que el gadolinio tiene un ordenamiento helimagnético , [5] pero otros defienden la opinión de larga data de que el gadolinio es un ferroimán convencional. [6]
Los elementos disprosio y erbio presentan dos transiciones magnéticas cada uno. Son paramagnéticos a temperatura ambiente, pero se vuelven helimagnéticos por debajo de sus respectivas temperaturas de Néel y luego se vuelven ferromagnéticos por debajo de sus temperaturas de Curie. Los elementos holmio , terbio y tulio muestran estructuras magnéticas aún más complicadas. [7]
También existe un ordenamiento antiferromagnético, que se desordena por encima de la temperatura de Néel . El cromo es algo así como un antiferromagnético simple, pero también tiene una modulación de onda de densidad de espín inconmensurable sobre la parte superior de la alternancia de espín simple arriba-abajo. [8] El manganeso (en la forma α-Mn) tiene 29 átomos de celda unitaria , lo que lleva a una disposición antiferromagnética compleja, pero proporcional a bajas temperaturas ( grupo espacial magnético P 4 2'm'). [9] [10] A diferencia de la mayoría de los elementos, que son magnéticos debido a los electrones, el ordenamiento magnético del cobre y la plata está dominado por el momento magnético nuclear mucho más débil (compárese el magnetón de Bohr y el magnetón nuclear ), lo que lleva a temperaturas de transición cercanas al cero absoluto . [11] [12]
Los elementos que se convierten en superconductores exhiben superdiamagnetismo por debajo de una temperatura crítica.
{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )