Directividad

Measure of how much of an antenna's signal is transmitted in one direction

Diagrama que muestra la directividad: la mayor densidad de potencia de esta antena está en la dirección del lóbulo rojo.

En electromagnetismo , la directividad es un parámetro de una antena o sistema óptico que mide el grado en el que la radiación emitida se concentra en una única dirección. Es la relación entre la intensidad de la radiación en una dirección dada desde la antena y la intensidad de la radiación promediada en todas las direcciones. ^[1] Por lo tanto, la directividad de un radiador isotrópico hipotético es 1, o 0 dBi .

La directividad de una antena es mayor que su ganancia por un factor de eficiencia, la eficiencia de radiación . ^[1] La directividad es una medida importante porque muchas antenas y sistemas ópticos están diseñados para radiar ondas electromagnéticas en una sola dirección o en un ángulo estrecho. Por el principio de reciprocidad , la directividad de una antena al recibir es igual a su directividad al transmitir.

La directividad de una antena real puede variar desde 1,76 dBi para un dipolo corto hasta 50 dBi para una antena parabólica grande . ^[2]

Definición

Diagrama que ilustra cómo se define la directividad. Muestra el patrón de radiación de una antena direccional (R, gris) que irradia máxima potencia a lo largo del eje z, y el patrón de una antena isótropa (R _iso , verde) con la misma potencia radiada total. La directividad se define como la relación entre la intensidad de señal máxima S radiada por la antena y la intensidad de señal S _iso radiada por la antena isótropa. Dado que la antena direccional radia la mayor parte de su potencia en un pequeño ángulo sólido alrededor del eje z, su intensidad de señal máxima es mucho mayor que la de la antena isótropa, que difunde la misma potencia en todas las direcciones. Por lo tanto, la directividad es mucho mayor que uno. $${\displaystyle G={S \over S_{\text{iso}}}}$$ ${\displaystyle G}$

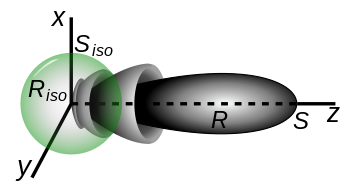
La directividad , , de una antena se define para todos los ángulos de incidencia de la misma. El término "ganancia directiva" ha sido desaprobado por el IEEE. Si no se especifica un ángulo relativo a la antena, se presume que la directividad se refiere al eje de máxima intensidad de radiación. ^[1] ${\displaystyle D}$

${\displaystyle D(\theta ,\phi )={\frac {U(\theta ,\phi )}{P_{\text{tot}}/\left(4\pi \right)}}.}$

Aquí y son el ángulo cenital y el ángulo acimutal respectivamente en los ángulos de coordenadas esféricas estándar ; es la intensidad de radiación , que es la potencia por unidad de ángulo sólido; y es la potencia radiada total. Las cantidades y satisfacen la relación ${\displaystyle \theta }$ ${\displaystyle \phi }$ ${\displaystyle U(\theta ,\phi )}$ ${\displaystyle P_{\text{tot}}}$ ${\displaystyle U(\theta ,\phi )}$ ${\displaystyle P_{\text{tot}}}$

${\displaystyle P_{\text{tot}}=\int _{\phi =0}^{\phi =2\pi }\int _{\theta =0}^{\theta =\pi }U\sin \theta \,d\theta \,d\phi ;}$

Es decir, la potencia radiada total es la potencia por unidad de ángulo sólido integrada sobre una superficie esférica. Como hay 4π estereorradianes en la superficie de una esfera, la cantidad representa la potencia promedio por unidad de ángulo sólido. ${\displaystyle P_{\text{tot}}}$ ${\displaystyle U(\theta ,\phi )}$ ${\displaystyle P_{\text{tot}}/(4\pi )}$

En otras palabras, la directividad es la intensidad de radiación de una antena en una combinación particular de coordenadas dividida por la que habría sido la intensidad de radiación si la antena hubiera sido una antena isótropa que irradiara la misma cantidad de potencia total al espacio. ${\displaystyle (\theta ,\phi )}$

Directividad , si no se especifica una dirección, es el valor de ganancia directiva máxima que se encuentra entre todos los ángulos sólidos posibles:

${\displaystyle {\begin{aligned}D&=\max \left({\frac {U}{P_{\text{tot}}/\left(4\pi \right)}}\right)\\[3pt]&={\frac {\left.U(\theta ,\phi )\right|_{\text{max}}}{{\frac {1}{4\pi }}\int _{0}^{2\pi }\int _{0}^{\pi }U(\theta ,\phi )\sin \theta \,d\theta \,d\phi }}.\end{aligned}}}$

En conjuntos de antenas

En un conjunto de antenas, la directividad es un cálculo complicado en el caso general. Para un conjunto lineal, la directividad siempre será menor o igual que el número de elementos. Para un conjunto lineal estándar (SLA) , donde el espaciado entre elementos es , la directividad es igual a la inversa del cuadrado de la norma 2 del vector de ponderación del conjunto, bajo el supuesto de que el vector de ponderación está normalizado de modo que su suma es la unidad. ^[3] ${\textstyle {\frac {\lambda }{2}}}$

${\displaystyle D_{\text{SLA}}={1 \over {\vec {w}}^{\textsf {H}}{\vec {w}}}\leq N}$

En el caso de un SLA ponderado uniformemente (no cónico), esto se reduce simplemente a N, el número de elementos de la matriz.

Para un conjunto plano, el cálculo de la directividad es más complicado y requiere la consideración de las posiciones de cada elemento del conjunto con respecto a todos los demás y con respecto a la longitud de onda. ^[4] Para un conjunto plano rectangular o hexagonalmente espaciado con elementos no isotrópicos, la directividad máxima se puede estimar utilizando la relación universal de apertura efectiva a directividad , ${\textstyle {\frac {\lambda ^{2}}{4\pi }}}$

${\displaystyle D=A_{e}{4{\pi } \over \lambda ^{2}}=Ndx\,dy\,\eta {4\pi \over \lambda ^{2}}}$

donde dx y dy son los espaciamientos de los elementos en las dimensiones x e y y es la "eficiencia de iluminación" de la matriz que explica el estrechamiento y el espaciado de los elementos en la matriz. Para una matriz no estrecha con elementos a un espaciado menor que, . Tenga en cuenta que para una matriz rectangular estándar (SRA) no estrecha, donde , esto se reduce a . Para una matriz rectangular estándar (SRA) no estrecha, donde , esto se reduce a un valor máximo de . La directividad de una matriz plana es el producto de la ganancia de la matriz , y la directividad de un elemento (asumiendo que todos los elementos son idénticos) solo en el límite a medida que el espaciado de los elementos se vuelve mucho mayor que lambda. En el caso de una matriz dispersa, donde el espaciado de los elementos , se reduce porque la matriz no está iluminada de manera uniforme. ${\displaystyle \eta }$ ${\displaystyle \lambda }$ ${\displaystyle \eta =1}$ ${\textstyle dx=dy={\lambda \over 2}}$ ${\displaystyle D\approx N\pi }$ ${\displaystyle dx=dy=\lambda }$ ${\displaystyle D_{\text{max}}\approx 4N\pi }$ ${\displaystyle >\lambda }$ ${\displaystyle \eta }$

Existe una razón física intuitiva para esta relación: básicamente, hay un número limitado de fotones por unidad de área que pueden ser capturados por las antenas individuales. Colocar dos antenas de alta ganancia muy cerca una de la otra (a menos de una longitud de onda) no duplica la ganancia, por ejemplo. Por el contrario, si las antenas están separadas por más de una longitud de onda, hay fotones que caen entre los elementos y no son capturados en absoluto. Por eso se debe tener en cuenta el tamaño de la apertura física.

Supongamos una matriz rectangular estándar no cónica de 16 × 16 (lo que significa que los elementos están espaciados a ). La ganancia de la matriz es dB. Si la matriz fuera cónica, este valor disminuiría. La directividad, asumiendo elementos isotrópicos, es 25,9 dBi. ^[5] Ahora supongamos elementos con una directividad de 9,0 dBi. La directividad no es 33,1 dBi, sino solo 29,2 dBi. ^[6] La razón de esto es que la apertura efectiva de los elementos individuales limita su directividad. Entonces, . Nótese que, en este caso, debido a que la matriz no es cónica, ¿por qué la ligera diferencia con 29,05 dBi? Los elementos alrededor del borde de la matriz no están tan limitados en su apertura efectiva como la mayoría de los elementos. ${\textstyle {\frac {\lambda }{2}}}$ ${\displaystyle 10\log _{10}(N)=10\log _{10}(256)=24.1}$ ${\textstyle D=A_{e}{\frac {4\pi }{\lambda ^{2}}}=Ndx\,dy\,\eta {\frac {4\pi }{\lambda ^{2}}}=N{\frac {\lambda }{2}}{\frac {\lambda }{2}}{\frac {4\pi }{\lambda ^{2}}}=N\pi }$ ${\displaystyle \eta =1}$ ${\displaystyle 10\log _{10}(N\pi )={}}$

Ahora, pasemos los elementos de la matriz al espaciado. Según la fórmula anterior, esperamos que la directividad alcance su pico en . El resultado real es 34,6380 dBi, apenas por debajo de los 35,0745 dBi ideales que esperábamos. ^[7] ¿Por qué la diferencia con el ideal? Si el espaciado en las dimensiones x e y es , entonces el espaciado a lo largo de las diagonales es , lo que crea pequeñas regiones en la matriz general donde se pierden los fotones, lo que lleva a . ${\displaystyle \lambda }$ ${\textstyle D=A_{e}{\frac {4\pi }{\lambda ^{2}}}=Ndx\,dy\,\eta {\frac {4\pi }{\lambda ^{2}}}=N\lambda \,\lambda \,{\frac {4\pi }{\lambda ^{2}}}=4N\pi }$ ${\displaystyle \lambda }$ ${\displaystyle \lambda {\sqrt {2}}}$ ${\displaystyle \eta <1}$

Ahora, pasemos al espaciado. El resultado debería converger a N veces la ganancia del elemento, o + 9 dBi = 33,1 dBi. El resultado real es, de hecho, 33,1 dBi. ^[8] ${\displaystyle 10\lambda }$ ${\displaystyle 10\log _{10}(N)}$

Para conjuntos de antenas, la expresión de forma cerrada para la directividad para un conjunto de fuentes isotrópicas en fase progresiva ^[9] estará dada por, ^[10]

${\displaystyle D={\frac {\left(\sum \limits _{n=1}^{N}I_{n}\right)^{2}}{\sum \limits _{m=1}^{N}\sum \limits _{n=1}^{N}I_{m}I_{n}e^{j(\beta _{m}-\beta _{n})}\operatorname {sinc} {\big (}2r_{mn}{\big )}}}}$

dónde,

${\displaystyle N}$es el número total de elementos en la apertura;

${\displaystyle \{x_{n},y_{n},z_{n}\}}$representa la ubicación de los elementos en el sistema de coordenadas cartesianas;

${\displaystyle I_{n}e^{j\beta _{n}}}$es el coeficiente de excitación complejo del elemento -; ${\displaystyle n^{\textrm {th}}}$

${\displaystyle \beta _{n}=-k(x_{n}\sin \theta _{\tau }\cos \phi _{\tau }+y_{n}\sin \theta _{\tau }\sin \phi _{\tau }+z_{n}\cos \theta _{\tau })}$es el componente de fase (fase progresiva);

${\textstyle k={\frac {2\pi }{\lambda }}}$es el número de onda;

${\displaystyle \{\theta _{\tau },\phi _{\tau }\}}$es la ubicación angular del objetivo de campo lejano;

${\displaystyle r_{mn}={\sqrt {(x_{m}-x_{n})^{2}+(y_{m}-y_{n})^{2}+(z_{m}-z_{n})^{2}}}}$es la distancia euclidiana entre el elemento y en la apertura, y ${\displaystyle m^{\textrm {th}}}$ ${\displaystyle n^{\textrm {th}}}$

${\textstyle \operatorname {sinc} (x)={\frac {1}{\pi x}}\sin(\pi x)}$

Se pueden realizar estudios adicionales sobre expresiones de directividad para varios casos, como si las fuentes son omnidireccionales (incluso en el entorno de matriz), como si el elemento-patrón prototipo toma la forma , y no se restringe a la fase progresiva. ^{[11] [12] [10] [13]} ${\textstyle \sin ^{\mu }\theta \cos ^{\nu }\theta ,\;\left(\mu >-1,\nu >-{\frac {1}{2}}\right)}$

Relación con el ancho de la viga

El ángulo sólido del haz , representado como , se define como el ángulo sólido por el que fluiría toda la potencia si la intensidad de radiación de la antena fuera constante en su valor máximo. Si se conoce el ángulo sólido del haz, entonces la directividad máxima se puede calcular como ${\displaystyle \Omega _{A}}$

${\displaystyle D={\frac {4\pi }{\Omega _{A}}},}$

que simplemente calcula la relación entre el ángulo sólido del haz y el ángulo sólido de una esfera.

El ángulo sólido del haz se puede calcular de forma aproximada para antenas con un lóbulo principal angosto y lóbulos menores muy insignificantes simplemente multiplicando los anchos de haz de media potencia (en radianes) en dos planos perpendiculares. El ancho de haz de media potencia es simplemente el ángulo en el que la intensidad de radiación es al menos la mitad de la intensidad de radiación máxima.

Los mismos cálculos se pueden realizar en grados en lugar de radianes:

${\displaystyle D\approx 4\pi {\frac {\left({\frac {180}{\pi }}\right)^{2}}{\Theta _{1d}\Theta _{2d}}}\approx {\frac {41253}{\Theta _{1d}\Theta _{2d}}},}$

donde es el ancho del haz de media potencia en un plano (en grados) y es el ancho del haz de media potencia en un plano en ángulo recto con el otro (en grados). ${\displaystyle \Theta _{1d}}$ ${\displaystyle \Theta _{2d}}$

En matrices planares, una mejor aproximación es

${\displaystyle D\approx {\frac {32400}{\Theta _{1d}\Theta _{2d}}}.}$

Para una antena con un haz cónico (o aproximadamente cónico) con un ancho de haz de media potencia de grados, entonces el cálculo integral elemental produce una expresión para la directividad como ${\displaystyle \theta }$

${\displaystyle D={\frac {2}{1-\cos {\frac {\theta }{2}}}}}$.

Expresión en decibeles

La directividad rara vez se expresa como un número sin unidades , sino más bien como una comparación de decibeles con una antena de referencia: ${\displaystyle D}$

${\displaystyle D_{\text{dB}}=10\log _{10}\left[{\frac {D}{D_{\text{reference}}}}\right].}$

La antena de referencia suele ser el radiador isótropo perfecto teórico , que irradia uniformemente en todas las direcciones y, por lo tanto, tiene una directividad de 1. Por lo tanto, el cálculo se simplifica a

${\displaystyle D_{\text{dBi}}=10\log _{10}D.}$

Otra antena de referencia común es el dipolo teórico de media onda perfecto , que irradia perpendicularmente a sí mismo con una directividad de 1,64:

${\displaystyle D_{\text{dBd}}\approx 10\log _{10}\left[{\frac {D}{1.64}}\right].}$

Contabilización de la polarización

Si se tiene en cuenta la polarización , se pueden calcular tres medidas adicionales:

Ganancia directiva parcial

La ganancia directiva parcial es la densidad de potencia en una dirección particular y para un componente particular de la polarización , dividida por la densidad de potencia promedio para todas las direcciones y todas las polarizaciones . Para cualquier par de polarizaciones ortogonales (como circular a la izquierda y circular a la derecha), las densidades de potencia individuales simplemente se suman para dar la densidad de potencia total. Por lo tanto, si se expresa como proporciones adimensionales en lugar de en dB, la ganancia directiva total es igual a la suma de las dos ganancias directivas parciales. ^[14]

Directividad parcial

La directividad parcial se calcula de la misma manera que la ganancia directiva parcial, pero sin tener en cuenta la eficiencia de la antena (es decir, suponiendo que se trata de una antena sin pérdidas). También es aditiva para polarizaciones ortogonales.

Ganancia parcial

La ganancia parcial se calcula de la misma manera que la ganancia, pero considerando solo una determinada polarización. Es igualmente aditiva para polarizaciones ortogonales.

En otras áreas

El término directividad también se utiliza con otros sistemas.

En los acopladores direccionales , la directividad es una medida de la diferencia en dB de la potencia de salida en un puerto acoplado, cuando la potencia se transmite en la dirección deseada, a la potencia de salida en el mismo puerto acoplado cuando la misma cantidad de potencia se transmite en la dirección opuesta. ^[15]

En acústica , se utiliza como una medida del patrón de radiación de una fuente que indica qué parte de la energía total de la fuente irradia en una dirección particular. En electroacústica, estos patrones incluyen comúnmente patrones polares de micrófono omnidireccionales, cardioides e hipercardioides. Se puede decir que un altavoz con un alto grado de directividad (patrón de dispersión estrecho) tiene un Q alto . ^[16]

Véase también

• Antena direccional

Referencias

1. IEEE Std 145-2013, Estándar IEEE para definiciones de términos para antenas, IEEE
2. Tutorial de antena
3. Van Trees, HL Procesamiento óptimo de matrices . págs. 60–63.
4. Van Trees, HL Procesamiento óptimo de matrices . págs. 247–249.
5. Van Trees, HL Procesamiento óptimo de matrices . págs. 247–249.
6. "Caja de herramientas del sistema de matriz en fase de MATLAB".
7. "Caja de herramientas del sistema de matriz en fase de MATLAB".
8. "Caja de herramientas del sistema de matriz en fase de MATLAB".
9. "Antenas de matriz en fase: análisis de floquet, síntesis, BFN y sistemas de matriz activa | Wiley". Wiley.com . Consultado el 29 de mayo de 2022 .
10. Das, Sudipta; Mandal, Durbadal; Ghoshal, Sakti Prasad; Kar, Rajib (febrero de 2017). "Generalización de expresiones de directividad para conjuntos de antenas". IEEE Transactions on Antennas and Propagation . 65 (2): 915–919. Bibcode :2017ITAP...65..915D. doi :10.1109/TAP.2016.2632738. ISSN  1558-2221. S2CID  19645584.
11. Das, Sudipta; Mandal, Durbadal; Kar, Rajib; Ghoshal, Sakti Prasad (julio de 2013). "Una expresión generalizada de forma cerrada de la directividad de conjuntos de antenas planares arbitrarios". IEEE Transactions on Antennas and Propagation . 61 (7): 3909–3911. Bibcode :2013ITAP...61.3909D. doi :10.1109/TAP.2013.2257652. ISSN  1558-2221. S2CID  44492351.
12. Kedar, Ashutosh; Ligthart, LP (febrero de 2019). "Características de barrido amplio de antenas de matriz en fase dispersa utilizando una expresión analítica para la directividad". IEEE Transactions on Antennas and Propagation . 67 (2): 905–914. Bibcode :2019ITAP...67..905K. doi :10.1109/TAP.2018.2880006. ISSN  0018-926X. S2CID  59620334.
13. Costa, Bruno Felipe; Abrão, Taufik (diciembre de 2018). "Expresión de directividad en forma cerrada para conjuntos de antenas volumétricas arbitrarias". IEEE Transactions on Antennas and Propagation . 66 (12): 7443–7448. arXiv : 1810.01487 . Bibcode :2018ITAP...66.7443C. doi :10.1109/TAP.2018.2869243. ISSN  1558-2221. S2CID  54196716.
14. Instituto de Ingenieros Eléctricos y Electrónicos, “El diccionario estándar IEEE de términos eléctricos y electrónicos”; 6.ª ed. Nueva York, NY, Instituto de Ingenieros Eléctricos y Electrónicos, c1997. IEEE Std 100-1996. ISBN 1-55937-833-6 [ed. Comité Coordinador de Normas 10, Términos y definiciones; Jane Radatz, (presidenta)] 
15. Nota de aplicación, acopladores direccionales Mini-Circuits
16. Definición de Q según AES Professional Audio Reference

Lectura adicional

• Coleman, Christopher (2004). "Conceptos básicos". Introducción a la ingeniería de radiofrecuencia . Cambridge University Press. ISBN 0-521-83481-3.