En el aprendizaje automático (ML), la agregación bootstrap , también llamada bagging (de b ootstrap agg regat ing ) o bootstrapping , es una metaheurística de conjunto para reducir principalmente la varianza (en contraposición al sesgo) . También puede mejorar la estabilidad y la precisión de los algoritmos de clasificación y regresión de ML , y puede reducir el sobreajuste . Aunque generalmente se aplica a los métodos de árboles de decisión , se puede utilizar con cualquier tipo de método. Bagging es un caso especial del enfoque de promedio de conjunto .
Dado un conjunto de entrenamiento estándar de tamaño , el bagging genera nuevos conjuntos de entrenamiento , cada uno de tamaño , mediante el muestreo de uniformemente y con reemplazo . Al muestrear con reemplazo, algunas observaciones pueden repetirse en cada . Si , entonces para grande se espera que el conjunto tenga la fracción (1 - 1/ e ) (~63,2%) de las muestras únicas de , siendo el resto duplicados. [1] Este tipo de muestra se conoce como muestra bootstrap . El muestreo con reemplazo asegura que cada bootstrap sea independiente de sus pares, ya que no depende de muestras elegidas previamente al muestrear. Luego, los modelos se ajustan utilizando las muestras bootstrap anteriores y se combinan promediando el resultado (para regresión) o votando (para clasificación).
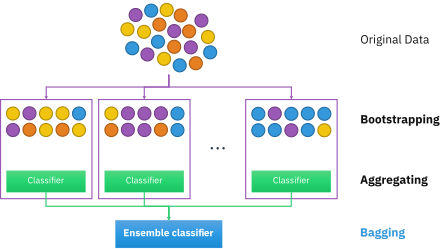
El bagging conduce a "mejoras para procedimientos inestables", [2] que incluyen, por ejemplo, redes neuronales artificiales , árboles de clasificación y regresión y selección de subconjuntos en regresión lineal . [3] Se ha demostrado que el bagging mejora el aprendizaje de preimagen. [4] [5] Por otro lado, puede degradar levemente el rendimiento de métodos estables como los k -vecinos más cercanos . [2]
Existen tres tipos de conjuntos de datos en la agregación bootstrap: los conjuntos de datos originales, bootstrap y out-of-bag. En cada sección siguiente se explicará cómo se crea cada conjunto de datos, excepto el conjunto de datos original. El conjunto de datos original es cualquier información que se proporcione.
El conjunto de datos bootstrap se crea seleccionando aleatoriamente objetos del conjunto de datos original. Además, debe tener el mismo tamaño que el conjunto de datos original. Sin embargo, la diferencia es que el conjunto de datos bootstrap puede tener objetos duplicados. A continuación, se muestra un ejemplo simple para demostrar cómo funciona junto con la siguiente ilustración:
Supongamos que el conjunto de datos original es un grupo de 12 personas cuyos nombres son Emily, Jessie, George, Constantine, Lexi, Theodore, John, James, Rachel, Anthony, Ellie y Jamal.
Al elegir un grupo de nombres al azar, supongamos que nuestro conjunto de datos bootstrap tenía James, Ellie, Constantine, Lexi, John, Constantine, Theodore, Constantine, Anthony, Lexi, Constantine y Theodore. En este caso, la muestra bootstrap contenía cuatro duplicados de Constantine y dos duplicados de Lexi y Theodore.
El conjunto de datos out-of-bag representa a las personas restantes que no estaban en el conjunto de datos bootstrap. Se puede calcular tomando la diferencia entre los conjuntos de datos originales y bootstrap. En este caso, las muestras restantes que no fueron seleccionadas son Emily, Jessie, George, Rachel y Jamal. Tenga en cuenta que, dado que ambos conjuntos de datos son conjuntos, al tomar la diferencia, los nombres duplicados se ignoran en el conjunto de datos bootstrap. La siguiente ilustración muestra cómo se realiza el cálculo:
La creación de los conjuntos de datos bootstrap y out-of-bag es crucial, ya que se utilizan para probar la precisión de un algoritmo de bosque aleatorio. Por ejemplo, un modelo que produce 50 árboles utilizando los conjuntos de datos bootstrap/out-of-bag tendrá una mayor precisión que si produjera 10 árboles. Dado que el algoritmo genera múltiples árboles y, por lo tanto, múltiples conjuntos de datos, la probabilidad de que un objeto quede fuera del conjunto de datos bootstrap es baja. Las siguientes secciones explican con más detalle cómo funciona el algoritmo de bosque aleatorio.
El siguiente paso del algoritmo implica la generación de árboles de decisión a partir del conjunto de datos bootstrap. Para lograrlo, el proceso examina cada gen/característica y determina para cuántas muestras la presencia o ausencia de la característica produce un resultado positivo o negativo. Esta información se utiliza luego para calcular una matriz de confusión , que enumera los verdaderos positivos, falsos positivos, verdaderos negativos y falsos negativos de la característica cuando se utiliza como clasificador. Estas características se clasifican luego de acuerdo con varias métricas de clasificación basadas en sus matrices de confusión. Algunas métricas comunes incluyen la estimación de la corrección positiva (calculada restando los falsos positivos de los verdaderos positivos), la medida de "bondad" y la ganancia de información . Estas características se utilizan luego para dividir las muestras en dos conjuntos: las que poseen la característica principal y las que no.
El diagrama siguiente muestra un árbol de decisión de profundidad dos que se utiliza para clasificar datos. Por ejemplo, a un punto de datos que exhibe la característica 1, pero no la característica 2, se le asignará un "No". A otro punto que no exhibe la característica 1, pero sí la característica 3, se le asignará un "Sí".
Este proceso se repite de forma recursiva en los niveles sucesivos del árbol hasta alcanzar la profundidad deseada. En la parte inferior del árbol, las muestras que dan positivo en la prueba de la característica final se clasifican generalmente como positivas, mientras que las que carecen de la característica se clasifican como negativas. Estos árboles se utilizan luego como predictores para clasificar los datos nuevos.
La siguiente parte del algoritmo implica introducir otro elemento de variabilidad entre los árboles bootstrap. Además de que cada árbol solo examina un conjunto de muestras bootstrap, solo se considera un número pequeño pero constante de características únicas al clasificarlos como clasificadores. Esto significa que cada árbol solo conoce los datos pertenecientes a un pequeño número constante de características y un número variable de muestras que es menor o igual al del conjunto de datos original. En consecuencia, es más probable que los árboles devuelvan una gama más amplia de respuestas, derivadas de un conocimiento más diverso. Esto da como resultado un bosque aleatorio , que posee numerosos beneficios sobre un solo árbol de decisión generado sin aleatoriedad. En un bosque aleatorio, cada árbol "vota" sobre si clasificar o no una muestra como positiva en función de sus características. Luego, la muestra se clasifica en función del voto mayoritario. Un ejemplo de esto se da en el diagrama a continuación, donde los cuatro árboles en un bosque aleatorio votan si un paciente con mutaciones A, B, F y G tiene cáncer o no. Dado que tres de los cuatro árboles votan sí, el paciente se clasifica como positivo para cáncer.

Debido a sus propiedades, los bosques aleatorios se consideran uno de los algoritmos de minería de datos más precisos, tienen menos probabilidades de sobreajustar sus datos y se ejecutan de manera rápida y eficiente incluso para grandes conjuntos de datos. [6] Son principalmente útiles para la clasificación en oposición a la regresión , que intenta establecer conexiones observadas entre variables estadísticas en un conjunto de datos. Esto hace que los bosques aleatorios sean particularmente útiles en campos como la banca, la atención médica, el mercado de valores y el comercio electrónico , donde es importante poder predecir resultados futuros en función de datos pasados. [7] Una de sus aplicaciones sería como una herramienta útil para predecir el cáncer en función de factores genéticos, como se ve en el ejemplo anterior.
Hay varios factores importantes a tener en cuenta al diseñar un bosque aleatorio. Si los árboles en los bosques aleatorios son demasiado profundos, aún puede ocurrir sobreajuste debido a la sobreespecificidad. Si el bosque es demasiado grande, el algoritmo puede volverse menos eficiente debido a un mayor tiempo de ejecución. Los bosques aleatorios tampoco suelen funcionar bien cuando se les dan datos dispersos con poca variabilidad. [7] Sin embargo, todavía tienen numerosas ventajas sobre algoritmos de clasificación de datos similares, como las redes neuronales , ya que son mucho más fáciles de interpretar y generalmente requieren menos datos para el entrenamiento. [ cita requerida ] Como componente integral de los bosques aleatorios, la agregación bootstrap es muy importante para los algoritmos de clasificación y proporciona un elemento crítico de variabilidad que permite una mayor precisión al analizar nuevos datos, como se analiza a continuación.
Si bien las técnicas descritas anteriormente utilizan bosques aleatorios y bagging (también conocido como bootstrapping), existen ciertas técnicas que se pueden utilizar para mejorar su tiempo de ejecución y votación, su precisión de predicción y su rendimiento general. Los siguientes son pasos clave para crear un bosque aleatorio eficiente:
Para la clasificación, utilice un conjunto de entrenamiento , un inductor y la cantidad de muestras de arranque como entrada. Genere un clasificador como salida [12]
para i = 1 a m { D' = muestra de arranque de D (muestra con reemplazo) Ci = I(D')}C*(x) = argmax #{i:Ci(x)=y} (la etiqueta predicha más frecuentemente es y) y∈Y Para ilustrar los principios básicos del ensacado, a continuación se presenta un análisis de la relación entre el ozono y la temperatura (datos de Rousseeuw y Leroy [ aclaración necesaria ] (1986), análisis realizado en R ).
La relación entre la temperatura y el ozono parece no ser lineal en este conjunto de datos, según el diagrama de dispersión. Para describir matemáticamente esta relación, se utilizan suavizadores LOESS (con un ancho de banda de 0,5). En lugar de construir un único suavizador para el conjunto de datos completo, se extrajeron 100 muestras de bootstrap . Cada muestra está compuesta por un subconjunto aleatorio de los datos originales y mantiene una apariencia de la distribución y variabilidad del conjunto maestro. Para cada muestra de bootstrap, se ajustó un suavizador LOESS. A continuación, se realizaron predicciones a partir de estos 100 suavizadores en todo el rango de datos. Las líneas negras representan estas predicciones iniciales. Las líneas carecen de concordancia en sus predicciones y tienden a sobreajustarse a sus puntos de datos: es evidente por el flujo inestable de las líneas.
Al tomar el promedio de 100 suavizadores, cada uno correspondiente a un subconjunto del conjunto de datos original, llegamos a un predictor empaquetado (línea roja). El flujo de la línea roja es estable y no se ajusta excesivamente a ningún punto de datos.
Ventajas:
Desventajas:
El concepto de agregación bootstrap se deriva del concepto de bootstrapping que fue desarrollado por Bradley Efron. [15] La agregación bootstrap fue propuesta por Leo Breiman, quien también acuñó el término abreviado "bagging" ( bootstrap agg regat ing ). Breiman desarrolló el concepto de bagging en 1994 para mejorar la clasificación mediante la combinación de clasificaciones de conjuntos de entrenamiento generados aleatoriamente. Argumentó que "si perturbar el conjunto de aprendizaje puede causar cambios significativos en el predictor construido, entonces el bagging puede mejorar la precisión". [3]
{{cite journal}}: Requiere citar revista |journal=( ayuda )CS1 maint: multiple names: authors list (link)