árbol m-ario

Estructura de datos de árbol en la que cada nodo tiene como máximo m hijos.

Un ejemplo de un árbol m-ario con m=5

En teoría de grafos , un árbol m -ario (para números enteros no negativos m ) (también conocido como n -ario , k -ario o árbol k -via ) es una arborescencia (o, para algunos autores, un árbol ordenado ) ^{[1] [2]} en el que cada nodo no tiene más de m hijos. Un árbol binario es un caso importante donde  m = 2; de manera similar, un árbol ternario es uno donde m = 3.

Tipos demetro-árboles arios

• Un árbol m -ario completo es un árbol m -ario donde dentro de cada nivel cada nodo tiene 0 o m hijos.
• Un árbol m -ario completo ^{[3] [4]} (o, con menos frecuencia, un árbol m -ario perfecto ^[5] ) es un árbol m -ario completo en el que todos los nodos de las hojas están a la misma profundidad.

Propiedades demetro-árboles arios

• Para un árbol m -ario con altura h , el límite superior para el número máximo de hojas es . ${\displaystyle m^{h}}$
• La altura h de un árbol m -ario no incluye el nodo raíz; un árbol que contiene solo un nodo raíz tiene una altura de 0.
• La altura de un árbol es igual a la profundidad máxima D de cualquier nodo del árbol.
• El número total de nodos en un árbol m -ario completo es , mientras que la altura h es ${\displaystyle N}$ ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$

$${\displaystyle {\begin{aligned}&{\frac {m^{h+1}-1}{m-1}}\geq N>{\frac {m^{h}-1}{m-1}}\\[8pt]&m^{h+1}\geq (m-1)\cdot N+1>m^{h}\\[8pt]&h+1\geq \log _{m}\left((m-1)\cdot N+1\right)>h\\[8pt]&h\geq \left\lceil \log _{m}((m-1)\cdot N+1)-1\right\rceil .\end{aligned}}}$$Según la definición de Big-Ω, la profundidad máxima $${\displaystyle D=h\geq \left\lceil \log _{m}((m-1)\cdot N+1)-1\right\rceil =O(\log _{m}n)=O(\log n/\log m).}$$

• La altura de un árbol m -ario completo con n nodos es . ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$
• El número total de posibles árboles m -arios con n nodos es (que es un número de Catalan ). ^[6] ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$

Métodos de recorrido parametro-árboles arios

Recorrer un árbol m -ario es muy similar a recorrer un árbol binario. El recorrido en preorden va al padre, al subárbol izquierdo y al subárbol derecho, y para recorrer en posorden va por el subárbol izquierdo, el subárbol derecho y el nodo padre. Para recorrer en orden, dado que hay más de dos hijos por nodo para m > 2 , se debe definir la noción de subárboles izquierdo y derecho . Un método común para establecer subárboles izquierdo/derecho es dividir la lista de nodos hijos en dos grupos. Al definir un orden en los m hijos de un nodo, los primeros nodos constituirían el subárbol izquierdo y los nodos constituirían el subárbol derecho. ${\textstyle \{1,\dots ,\lfloor {\frac {m}{2}}\rfloor \}}$ ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$

Convertir unmetroárbol -ario a árbol binario

Un ejemplo de conversión de un árbol m-ario a un árbol binario. m=6

El uso de una matriz para representar un árbol m -ario es ineficiente, porque la mayoría de los nodos en aplicaciones prácticas contienen menos de m hijos. Como resultado, este hecho conduce a una matriz dispersa con un gran espacio sin usar en la memoria. Convertir un árbol m- ario arbitrario en un árbol binario solo aumentaría la altura del árbol por un factor constante y no afectaría la complejidad temporal general del peor caso. En otras palabras, dado que . ${\textstyle O(\log _{m}n)\equiv O(\log _{2}n)}$ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$

Primero, vinculamos todos los nodos hijos inmediatos de un nodo padre dado para formar una lista de enlaces. Luego, mantenemos el enlace del padre al primer hijo (es decir, el más a la izquierda) y eliminamos todos los demás enlaces al resto de los hijos. Repetimos este proceso para todos los hijos (si tienen hijos) hasta que hayamos procesado todos los nodos internos y hayamos rotado el árbol 45 grados en el sentido de las agujas del reloj. El árbol obtenido es el árbol binario deseado obtenido a partir del árbol m -ario dado.

Métodos de almacenamientometro-árboles arios

Matrices

Un ejemplo de almacenamiento de un árbol m-ario con m=3 en una matriz

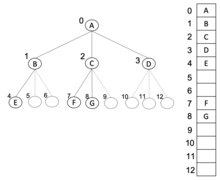
Los árboles m -arios también se pueden almacenar en orden de amplitud como una estructura de datos implícita en matrices y, si el árbol es un árbol m -ario completo, este método no desperdicia espacio. En esta disposición compacta, si un nodo tiene un índice i , su c -ésimo hijo en el rango {1,…, m } se encuentra en el índice , mientras que su padre (si lo hay) se encuentra en el índice (asumiendo que la raíz tiene índice cero, es decir, una matriz basada en 0). Este método se beneficia de un almacenamiento más compacto y una mejor localidad de referencia , particularmente durante un recorrido de preorden. La complejidad espacial de este método es . ${\displaystyle m\cdot i+c}$ ${\textstyle \left\lfloor {\frac {i-1}{m}}\right\rfloor }$ ${\displaystyle O(m^{n})}$

Basado en punteros

Cada nodo tendría una matriz interna para almacenar punteros a cada uno de sus hijos: ${\displaystyle m}$

Implementación basada en punteros del árbol m-ario donde m = 4.

En comparación con la implementación basada en matrices, este método de implementación tiene una complejidad espacial superior de . ${\displaystyle O(m\cdot n)}$

Enumeración demetro-árboles arios

Enumerar todos los árboles m -arios posibles es útil en muchas disciplinas como una forma de comprobar hipótesis o teorías. La representación adecuada de los objetos de árboles m- arios puede simplificar en gran medida el proceso de generación. Se puede construir una representación de secuencia de bits utilizando la búsqueda en profundidad de un árbol m -ario con n nodos que indique la presencia de un nodo en un índice dado utilizando valores binarios. Por ejemplo, la secuencia de bits x=1110000100010001000 representa un árbol 3-ario con n=6 nodos como se muestra a continuación.

Árbol 3-ario con secuencia de bits de 1110000100010001000 y secuencia cero simple de 004433

El problema con esta representación es que listar todas las cadenas de bits en orden lexicográfico significaría que dos cadenas sucesivas podrían representar dos árboles que son lexicográficamente muy diferentes. Por lo tanto, la enumeración sobre cadenas binarias no necesariamente resultaría en una generación ordenada de todos los árboles m- arios. ^[7] Una mejor representación se basa en una cadena entera que indica el número de ceros entre unos sucesivos, conocida como Secuencia Cero Simple . es una Secuencia Cero Simple que corresponde a la secuencia de bits donde j es el número de ceros necesarios al final de la secuencia para hacer que la cadena tenga la longitud apropiada. Por ejemplo, es la representación de secuencia cero simple de la figura anterior. Una representación más compacta de 00433 es , que se llama secuencia cero , cuyas bases duplicadas no pueden ser adyacentes. Esta nueva representación permite construir una siguiente secuencia válida en . Una secuencia cero simple es válida si Es decir que el número de ceros en la secuencia de bits de un árbol m -ario no puede exceder el número total de punteros nulos (es decir, punteros sin ningún nodo hijo adjunto a ellos). Esta suma pone restricciones en los nodos para que haya espacio para agregarlos sin crear una estructura no válida (es decir, tener un puntero nulo disponible para adjuntarle el último nodo). ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ ${\displaystyle 1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433}$ ${\displaystyle 0^{2}4^{1}3^{2}}$ ${\displaystyle O(1)}$ $${\displaystyle \sum _{i=1}^{i=j}s_{i}\leq (m-1)j\qquad \forall j\leq n-1.}$$ ${\displaystyle n-1}$ ${\displaystyle n^{t}h}$

La siguiente tabla muestra la lista de todas las secuencias cero simples válidas de todos los árboles 3 -arios con 4 nodos:

A partir de la parte inferior derecha de la tabla (es decir, "000"), hay una plantilla de estructura principal que rige la generación de los posibles árboles ordenados desde "000" hasta "006". La plantilla de estructura principal para este grupo ("00X") se muestra a continuación, donde se agrega un nodo adicional en las posiciones etiquetadas como "x".

Una vez que se hayan agotado todas las posiciones posibles en la plantilla de la red troncal, se construirá una nueva plantilla desplazando el tercer nodo una posición hacia la derecha como se muestra a continuación, y se realizará la misma enumeración hasta que se agoten todas las posiciones posibles etiquetadas como "X".

Volviendo a la tabla de enumeración de todos los árboles m -arios, donde y , podemos observar fácilmente que el salto aparente de "006" a "010" se puede explicar trivialmente de manera algorítmica como se muestra a continuación: ${\displaystyle m=3}$ ${\displaystyle n=4}$

El pseudocódigo para esta enumeración se proporciona a continuación: ^[7]

Procedimiento NEXT( s 1 , s 2 , …, s n −1 ) si  s i = 0 para todo i  entonces finalizado de lo contrario  i ← máx { i | s i > 0} s i ← s i − 1 si  i < n − 1 entonces  s i ← ( i + 1) ⋅ ( m − 1) − suma( s j ) fin si  para  j ← i + 2, i + 3, …, n − 1 s j ← k − 1 fin si fin

Enumeración sin bucles

Un algoritmo de generación que toma el tiempo del peor caso se llama sin bucles ya que la complejidad temporal no puede involucrar un bucle o recursión. Se dice que la enumeración sin bucles de árboles m- arios no tiene bucles si después de la inicialización, genera objetos de árbol sucesivos en . Para un árbol m- ario dado T con uno de sus nodos y su -ésimo hijo, se realiza una rotación a la izquierda en t haciendo que el nodo raíz y haciendo que y todos sus subárboles sean hijos de , además asignamos los hijos más a la izquierda de a y el hijo más a la derecha de permanece adjunto a él mientras se promueve a raíz, como se muestra a continuación: ${\displaystyle O(1)}$ ${\displaystyle O(1)}$ ${\displaystyle a}$ ${\displaystyle d}$ ${\displaystyle t}$ ${\displaystyle a}$ ${\displaystyle d}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle m-1}$ ${\displaystyle d}$ ${\displaystyle a}$ ${\displaystyle d}$ ${\displaystyle d}$

Convertir un árbol m-ario en un árbol izquierdo  para  i = 1... n : para  t = 2... m : mientras  t sea hijo del nodo en la profundidad i ≠ 1: Rotación de Lt en nodos a profundidad i  fin mientras  fin para  fin para

Una rotación t-derecha en d es la inversa de esta operación. La cadena izquierda de T es una secuencia de nodos tal que es la raíz y todos los nodos excepto tienen un hijo conectado a su puntero más a la izquierda (es decir, ). Cualquier árbol m- ario se puede transformar en un árbol de cadena izquierda utilizando una secuencia de rotaciones t-izquierdas finitas para t desde 2 hasta m . Específicamente, esto se puede hacer realizando rotaciones t-izquierdas en cada nodo hasta que todos sus subárboles se vuelvan nulos en cada profundidad. Luego, la secuencia del número de rotaciones t-izquierdas realizadas en la profundidad i denotada por define una palabra de código de un árbol m- ario que se puede recuperar realizando la misma secuencia de rotaciones t-derechas. ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{n}}$ ${\displaystyle m[1]}$ ${\displaystyle x_{i}}$ ${\displaystyle m-1}$ ${\displaystyle c_{i}}$

Sea la tupla de la que representa el número de rotaciones L-2 , L-3 , ..., Lm que han ocurrido en la raíz (es decir, i = 1). Entonces, es el número de rotaciones Lt requeridas a la profundidad i . ${\displaystyle m-1}$ ${\displaystyle c_{1},c_{2},\dots ,c_{m-1}}$ ${\displaystyle c_{(i-1)(m-1)+t-1}}$

Capturar los recuentos de rotaciones a la izquierda en cada profundidad es una forma de codificar un árbol m -ario. Por lo tanto, enumerar todas las codificaciones legales posibles nos ayudaría a generar todos los árboles m -arios para un m y n dados . Pero no todas las secuencias de m números enteros no negativos representan un árbol m-ario válido. Una secuencia de números enteros no negativos es una representación válida de un árbol m -ario si y solo si ^[8] ${\displaystyle c_{i}}$ ${\displaystyle (n-1)\cdot (m-1)+1}$ $${\displaystyle \sum _{i=j}^{n}\sum _{t=2}^{m}c_{(i-1)(m-1)+t-1}\qquad \leq n-j,\qquad \forall j\in 0\dots n.}$$

La representación lexicográficamente más pequeña de una palabra código de un m-ario con n nodos es todos ceros y la más grande es n −1 unos seguidos de m −1 ceros a su derecha.

Inicialización c[i] a cero para todos los i desde 1 hasta n ⋅( k − 1) p[i] establecido en n − 1 para i de 1 a n suma ← 0 j ← m − 1Condición de terminación Terminar cuando c[1] = n − 1Procedimiento SIGUIENTE [8]  suma ← suma + 1 − c [ j + 1] c [j] ← c [ j ] + 1 si  p [ q [ j ]] > p [ q [ j + 1]] + 1 entonces  p [ q [ j ]] ← p [ q [ j + 1]] + 1 fin si  p [ q [ j + c [ j ]]] ← p [ q [ j ]] c [ j + 1] ← 0 si  suma = p [ q [ j ]] entonces  j ← j − 1 de lo contrario  p [ n ] ← suma  j ← m − 1 fin si fin

Solicitud

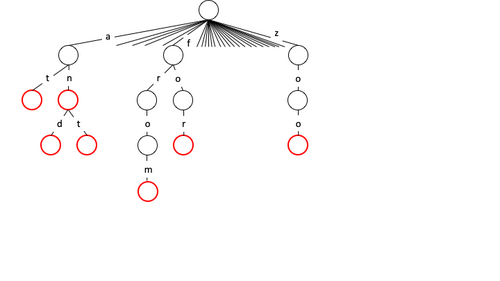
Una de las aplicaciones del árbol m -ario es la creación de un diccionario para la validación de cadenas aceptables. Para ello, sea m igual al número de alfabetos válidos (por ejemplo, el número de letras del alfabeto inglés ) con la raíz del árbol representando el punto de partida. De manera similar, cada uno de los hijos puede tener hasta m hijos que representan el siguiente carácter posible en la cadena. Por lo tanto, los caracteres a lo largo de las rutas pueden representar claves válidas marcando el carácter final de las claves como "nodo terminal". Por ejemplo, en el ejemplo siguiente "at" y "and" son cadenas de claves válidas con "t" y "d" marcados como nodos terminales. Los nodos terminales pueden almacenar información adicional para asociarla con una clave dada. Existen formas similares de construir un diccionario de este tipo utilizando B-tree , Octree y/o trie .

Véase también

• Factor de ramificación
• Árbol binario de hijo izquierdo y hermano derecho
• Árbol binario

Referencias

1. Li, Liwu (1998). Java: Estructuras de datos y programación. Sección 8.1.2.1, Árboles multiarios : Springer. doi :10.1007/978-3-642-95851-9. ISBN 978-3-642-95853-3. S2CID  708416 . Consultado el 20 de julio de 2023 .{{cite book}}: CS1 maint: location (link)
2. Stanley, Richard P. (2011). Combinatoria enumerativa, volumen I. Apéndice: Terminología de la teoría de grafos: Cambridge University Press. p. 573. ISBN 978-1-107-60262-5. Recuperado el 20 de julio de 2023 .
3. Gross, Jonathan L.; Yellen, Jay; Anderson, Mark (2018). Teoría de grafos y sus aplicaciones (3.ª ed.). Sección 3.2, Árboles con raíces, árboles ordenados y árboles binarios : CRC Press. p. 132. ISBN 978-1-4822-4948-4.{{cite book}}: CS1 maint: location (link)
4. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2022). Introducción a los algoritmos (4.ª ed.). Sección B.5.3, Árboles binarios y posicionales : MIT Press. p. 1174. ISBN 9780262046305. Recuperado el 20 de julio de 2023 .{{cite book}}: CS1 maint: location (link)
5. Schumacher, Patrik (2012). "Excursión: teoría de redes". La autopoiesis de la arquitectura: una nueva agenda para la arquitectura, vol. II. Wiley. pág. 103. ISBN 978-0-470-66616-6.
6. Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). Matemáticas concretas: una base para la informática (2.ª ed.). AIP.
7. Baronaigien, Dominique Roelants van (2000). "Generación sin bucles de árboles K-arios". Journal of Algorithms . 35 (1): 100–107. doi :10.1006/jagm.1999.1073.
8. Korsh, James F (1994). "Generación sin bucles de secuencias de árboles k-arios". Information Processing Letters . 52 (5). Elsevier: 243–247. doi :10.1016/0020-0190(94)00149-9.

• Storer, James A. (2001). Introducción a las estructuras de datos y algoritmos . Birkhäuser Boston. ISBN 3-7643-4253-6.

Enlaces externos

• Árboles N-arios, Bruno R. Preiss, Ph.D, P.Eng.