En teoría de juegos , el juego del ciempiés , introducido por primera vez por Robert Rosenthal en 1981, es un juego de forma extensiva en el que dos jugadores se turnan para elegir tomar una parte ligeramente mayor de un bote creciente o pasar el bote al otro jugador. Los pagos están dispuestos de modo que si uno pasa el bote a su oponente y el oponente se lo lleva en la siguiente ronda, uno recibe un poco menos que si hubiera tomado el bote en esta ronda, pero después de un cambio adicional el pago potencial será más alto. Por lo tanto, aunque en cada ronda un jugador tiene un incentivo para llevarse el bote, sería mejor que esperara. Aunque el tradicional juego del ciempiés tenía un límite de 100 rondas (de ahí el nombre), cualquier juego con esta estructura pero con diferente número de rondas se llama juego del ciempiés.
El equilibrio perfecto en subjuegos único (y cada equilibrio de Nash ) de estos juegos da como resultado que el primer jugador se lleve el bote en la primera ronda del juego; sin embargo, en pruebas empíricas , relativamente pocos jugadores lo hacen y, como resultado, logran un pago mayor que en el equilibrio perfecto en subjuegos y de Nash. Estos resultados sirven para mostrar que los equilibrios perfectos en subjuegos y los equilibrios de Nash no logran predecir el juego humano en algunas circunstancias. El juego Ciempiés se utiliza comúnmente en cursos y textos de introducción a la teoría de juegos para resaltar el concepto de inducción hacia atrás y la eliminación iterada de estrategias dominadas , que muestran una forma estándar de brindar una solución al juego.
Una posible versión del juego del ciempiés podría jugarse de la siguiente manera:
Considere dos jugadores: Alice y Bob . Alice se mueve primero. Al comienzo del juego, Alice tiene dos montones de monedas frente a ella: un montón contiene 4 monedas y el otro montón contiene 1 moneda. Cada jugador tiene dos movimientos disponibles: "tomar" la pila más grande de monedas y darle la pila más pequeña al otro jugador o "empujar" ambas pilas a través de la mesa hacia el otro jugador. Cada vez que los montones de monedas pasan por la mesa, la cantidad de monedas en cada montón se duplica. Por ejemplo, supongamos que Alice elige "empujar" las pilas en su primer movimiento, entregándole las pilas de 1 y 4 monedas a Bob, duplicándolas a 2 y 8. Bob ahora podría usar su primer movimiento para "tomar" las monedas. pila de 8 monedas y darle 2 monedas a Alice, o puede "empujar" las dos pilas a través de la mesa nuevamente hacia Alice, aumentando nuevamente el tamaño de las pilas a 4 y 16 monedas. El juego continúa durante un número fijo de rondas o hasta que un jugador decide terminar el juego embolsándose un montón de monedas.
La adición de monedas se considera una externalidad , ya que ninguno de los jugadores la aporta.
El juego del ciempiés puede escribirse como donde y . Los jugadores y suplentes, comenzando con el jugador , pueden en cada turno realizar un movimiento con un máximo de rondas. El juego termina cuando se juega por primera vez; de lo contrario, al realizar movimientos, si nunca se juega.
Supongamos que el juego termina en la ronda y el jugador realiza el movimiento final. Entonces el resultado del juego se define de la siguiente manera:
Aquí, denota el otro jugador.
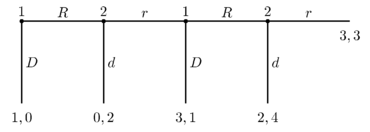
Las herramientas estándar de la teoría de juegos predicen que el primer jugador desertará en la primera ronda y se quedará con el montón de monedas. En el juego del ciempiés, una estrategia pura consiste en un conjunto de acciones (una para cada punto de elección del juego, aunque es posible que algunos de estos puntos de elección nunca se alcancen) y una estrategia mixta es una distribución de probabilidad sobre las posibles estrategias puras. Hay varios equilibrios de Nash de estrategias puras del juego del ciempiés e infinitos equilibrios de Nash de estrategias mixtas. Sin embargo, sólo existe un equilibrio perfecto en subjuegos (un refinamiento popular del concepto de equilibrio de Nash).
En el equilibrio perfecto único en subjuegos, cada jugador elige desertar en cada oportunidad. Esto, por supuesto, significa deserción en la primera etapa. Sin embargo, en los equilibrios de Nash, las acciones que se tomarían después de las oportunidades de elección iniciales (aunque nunca se alcancen porque el primer jugador abandona inmediatamente) pueden ser cooperativas.
La deserción del primer jugador es el único equilibrio perfecto en subjuegos y, requerido por cualquier equilibrio de Nash , puede establecerse mediante inducción hacia atrás . Supongamos que dos jugadores llegan a la ronda final del juego; al segundo jugador le irá mejor si deserta y se lleva una parte ligeramente mayor del bote. Como suponemos que el segundo jugador desertará, al primer jugador le irá mejor si deserta en la penúltima ronda, obteniendo una recompensa ligeramente mayor que la que habría recibido si hubiera permitido que el segundo jugador desertara en la última ronda. Pero sabiendo esto, el segundo jugador debería desertar en la penúltima ronda, obteniendo una recompensa ligeramente mayor que la que habría recibido al permitir que el primer jugador desertara en la penúltima ronda. Este razonamiento avanza hacia atrás a través del árbol del juego hasta que se concluye que la mejor acción es que el primer jugador deserte en la primera ronda. El mismo razonamiento puede aplicarse a cualquier nodo del árbol del juego.
Para un juego que termina después de cuatro rondas, este razonamiento es el siguiente. Si llegáramos a la última ronda del juego, el jugador 2 haría mejor si eligiera d en lugar de r , recibiendo 4 monedas en lugar de 3. Sin embargo, dado que 2 elegirá d , 1 debería elegir D en la penúltima ronda. , recibiendo 3 en lugar de 2. Dado que 1 elegiría D en la penúltima ronda, 2 debería elegir d en la antepenúltima ronda, recibiendo 2 en lugar de 1. Pero dado esto, el jugador 1 debería elegir D en la primera ronda. , recibiendo 1 en lugar de 0.
Hay un gran número de equilibrios de Nash en un juego de ciempiés, pero en cada uno de ellos, el primer jugador deserta en la primera ronda y el segundo jugador deserta en la siguiente ronda con suficiente frecuencia como para disuadir al primer jugador de pasar. Estar en un equilibrio de Nash no requiere que las estrategias sean racionales en cada punto del juego como en el equilibrio perfecto en subjuegos. Esto significa que las estrategias que son cooperativas en las rondas posteriores del juego que nunca se alcanzan aún podrían estar en un equilibrio de Nash. En el ejemplo anterior, un equilibrio de Nash es que ambos jugadores deserten en cada ronda (incluso en las rondas posteriores que nunca se alcanzan). Otro equilibrio de Nash es que el jugador 1 deserte en la primera ronda, pero pase a la tercera ronda y que el jugador 2 deserte en cualquier oportunidad.
Varios estudios han demostrado que el juego del equilibrio de Nash (y también el equilibrio perfecto en subjuegos) rara vez se observa. En cambio, los sujetos muestran regularmente una cooperación parcial, jugando "R" (o "r") durante varios movimientos antes de elegir finalmente "D" (o "d"). También es raro que los sujetos cooperen durante todo el juego. Para ejemplos, ver McKelvey y Palfrey (1992), Nagel y Tang (1998) o Krockow et al. (2016) [1] para una encuesta. Los académicos han investigado el efecto de aumentar lo que está en juego. Al igual que con otros juegos, por ejemplo el juego del ultimátum , a medida que aumentan las apuestas, el juego se acerca (pero no alcanza) el juego de equilibrio de Nash. [2] Dado que los estudios empíricos han producido resultados que son inconsistentes con el análisis de equilibrio tradicional, se han ofrecido varias explicaciones de este comportamiento. Para explicar los datos experimentales, necesitamos algunos agentes altruistas o algunos agentes racionales limitados.
Una razón por la que las personas pueden desviarse del comportamiento de equilibrio es si algunas son altruistas . La idea básica es que tienes una cierta probabilidad en cada juego de jugar contra un agente altruista y si esta probabilidad es lo suficientemente alta, deberías desertar en la última ronda en lugar de en la primera. Si suficientes personas son altruistas, sacrificar la recompensa de la deserción en la primera ronda vale el precio para determinar si su oponente es altruista o no.
McKelvey y Palfrey (1992) crean un modelo con algunos agentes altruistas y algunos agentes racionales que terminarán jugando una estrategia mixta (es decir, juegan en múltiples nodos con cierta probabilidad). Para que los datos experimentales coincidan bien, alrededor del 5% de los jugadores deben ser altruistas en el modelo. Elmshauser (2022) [3] muestra que un modelo que incluye agentes altruistas y agentes reacios a la incertidumbre (en lugar de agentes racionales) explica aún mejor los datos experimentales. Algunos experimentos intentaron ver si los jugadores que pasaban mucho también serían los agentes más altruistas en otros juegos u otras situaciones de la vida (ver, por ejemplo, Pulford et al [4] o Gamba y Regner (2019) [5], quienes evaluaron la orientación al valor social . ). Los jugadores que pasaban mucho eran efectivamente más altruistas, pero la diferencia no era enorme.
Rosenthal (1981) sugirió que si uno tiene razones para creer que su oponente se desviará del comportamiento de Nash, entonces puede ser ventajoso no desertar en la primera ronda. Otra posibilidad implica un error. Si existe una posibilidad significativa de error en la acción, tal vez porque su oponente no ha razonado completamente a través de la inducción hacia atrás, puede ser ventajoso (y racional) cooperar en las rondas iniciales. El equilibrio de respuesta cuántica de McKelvey y Palfrey (1995) [6] creó un modelo con agentes jugando al equilibrio de Nash con errores y lo aplicaron al juego del ciempiés.
Otro modelo capaz de explicar los comportamientos en el juego del ciempiés es el modelo de nivel k, que es una teoría de la jerarquía cognitiva : un jugador L0 juega aleatoriamente, el jugador L1 responde mejor al jugador L0, el jugador L2 responde mejor al jugador L1 y pronto. En muchos juegos, los estudiosos observaron que la mayoría de los jugadores eran jugadores de L2 o L3, lo que concuerda con los datos experimentales del juego del ciempiés. García-Pola et al. (2020) [7] concluyó a partir de un experimento que la mayoría de los jugadores juegan siguiendo una lógica de nivel k o una lógica de respuesta cuántica.
Sin embargo, Parco, Rapoport y Stein (2002) ilustraron que el nivel de incentivos financieros puede tener un efecto profundo en el resultado de un juego de tres jugadores: cuanto mayores sean los incentivos para la desviación, mayor será la propensión a aprender una conducta en un juego único repetido. -jugar al diseño experimental para avanzar hacia el equilibrio de Nash.
Palacios-Huerta y Volij (2009) encuentran que los ajedrecistas expertos juegan de manera diferente a los estudiantes universitarios. Con un Elo en aumento , la probabilidad de continuar el juego disminuye; Todos los Grandes Maestros del experimento se detuvieron ante la primera oportunidad. Concluyen que los jugadores de ajedrez están familiarizados con el uso del razonamiento de inducción hacia atrás y, por tanto, necesitan menos aprendizaje para alcanzar el equilibrio. Sin embargo, en un intento de replicar estos hallazgos, Levitt, List y Sadoff (2010) encuentran resultados fuertemente contradictorios: ninguno de los dieciséis Grandes Maestros detuvo el juego en el primer nodo.
La investigación cualitativa realizada por Krockow et al., que empleó protocolos de pensamiento en voz alta que requerían que los jugadores en un juego de Ciempiés expresaran su razonamiento durante el juego, indicó una variedad de sesgos de decisión, como el sesgo de acción o el sesgo de finalización, que pueden impulsar elecciones irracionales en el juego. juego. [8]
Al igual que el dilema del prisionero , este juego presenta un conflicto entre el interés propio y el beneficio mutuo. Si se pudiera hacer cumplir, ambos jugadores preferirían que cooperaran durante todo el juego. Sin embargo, el interés propio de un jugador o la desconfianza de los jugadores pueden interferir y crear una situación en la que a ambos les vaya peor que si hubieran cooperado ciegamente. Aunque el dilema del prisionero ha recibido considerable atención por este hecho, el juego del ciempiés ha recibido relativamente menos.
Además, Binmore (2005) ha argumentado que algunas situaciones del mundo real pueden describirse mediante el juego Centipede. Un ejemplo que presenta es el intercambio de bienes entre partes que desconfían entre sí. Otro ejemplo que Binmore (2005) compara con el juego del ciempiés es el comportamiento de apareamiento de una lubina hermafrodita que se turna para intercambiar huevos para fertilizar. En estos casos, encontramos que la cooperación es abundante.
Dado que los beneficios de cierta cooperación en el juego del ciempiés son mucho mayores que la deserción inmediata, las soluciones "racionales" dadas por la inducción hacia atrás pueden parecer paradójicas. Esto, junto con el hecho de que los sujetos experimentales cooperan regularmente en el juego del ciempiés, ha provocado un debate sobre la utilidad de las idealizaciones involucradas en las soluciones de inducción hacia atrás, ver Aumann (1995, 1996) y Binmore (1996).