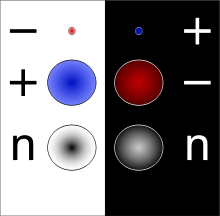
En física de partículas , cada tipo de partícula de materia "ordinaria" (a diferencia de la antimateria ) está asociada a una antipartícula con la misma masa pero con cargas físicas opuestas (como la carga eléctrica ). Por ejemplo, la antipartícula del electrón es el positrón (también conocido como antielectrón). Mientras que el electrón tiene una carga eléctrica negativa, el positrón tiene una carga eléctrica positiva, y se produce de forma natural en ciertos tipos de desintegración radiactiva . Lo contrario también es cierto: la antipartícula del positrón es el electrón.
Algunas partículas, como el fotón , son su propia antipartícula. De lo contrario, para cada par de antipartículas asociadas, una se designa como la partícula normal (la que se encuentra en la materia con la que se suele interactuar en la vida diaria). La otra (que suele recibir el prefijo "anti-") se designa como la antipartícula .
Los pares partícula-antipartícula pueden aniquilarse entre sí, produciendo fotones ; dado que las cargas de la partícula y la antipartícula son opuestas, la carga total se conserva. Por ejemplo, los positrones producidos en la desintegración radiactiva natural se aniquilan rápidamente con los electrones, produciendo pares de rayos gamma , un proceso que se aprovecha en la tomografía por emisión de positrones .
Las leyes de la naturaleza son casi simétricas con respecto a las partículas y antipartículas. Por ejemplo, un antiprotón y un positrón pueden formar un átomo de antihidrógeno , que se cree que tiene las mismas propiedades que un átomo de hidrógeno . Esto lleva a la pregunta de por qué la formación de la materia después del Big Bang resultó en un universo compuesto casi en su totalidad de materia, en lugar de ser una mezcla mitad materia y mitad antimateria . El descubrimiento de la violación de la paridad de carga ayudó a arrojar luz sobre este problema al mostrar que esta simetría, que originalmente se pensó que era perfecta, era solo aproximada. La pregunta sobre cómo la formación de la materia después del Big Bang resultó en un universo compuesto casi en su totalidad de materia sigue sin respuesta, y las explicaciones hasta ahora no son verdaderamente satisfactorias, en general.
Como la carga se conserva , no es posible crear una antipartícula sin destruir otra partícula de la misma carga (como es, por ejemplo, el caso cuando las antipartículas se producen naturalmente mediante la desintegración beta o la colisión de rayos cósmicos con la atmósfera de la Tierra), o mediante la creación simultánea de una partícula y su antipartícula (producción de pares), lo que puede ocurrir en aceleradores de partículas como el Gran Colisionador de Hadrones del CERN .
Las partículas y sus antipartículas tienen cargas iguales y opuestas, de modo que una partícula sin carga también da lugar a una antipartícula sin carga. En muchos casos, la antipartícula y la partícula coinciden: pares de fotones , bosones Z 0 ,π0 Los mesones , los gravitones hipotéticos y algunos WIMP hipotéticos se autoaniquilan. Sin embargo, las partículas eléctricamente neutras no tienen por qué ser idénticas a sus antipartículas: por ejemplo, el neutrón y el antineutrón son distintos.
En 1932, poco después de la predicción de los positrones por Paul Dirac , Carl D. Anderson descubrió que las colisiones de rayos cósmicos producían estas partículas en una cámara de niebla , un detector de partículas en el que los electrones (o positrones) en movimiento dejan rastros a medida que se mueven a través del gas. La relación carga eléctrica-masa de una partícula se puede medir observando el radio de curvatura de su trayectoria en la cámara de niebla en un campo magnético . Los positrones, debido a la dirección en la que se curvaban sus trayectorias, al principio se confundieron con electrones que viajaban en la dirección opuesta. Las trayectorias de los positrones en una cámara de niebla trazan la misma trayectoria helicoidal que un electrón, pero giran en la dirección opuesta con respecto a la dirección del campo magnético debido a que tienen la misma magnitud de relación carga-masa pero con carga opuesta y, por lo tanto, relaciones carga-masa con signo opuesto.
El antiprotón y el antineutrón fueron descubiertos por Emilio Segrè y Owen Chamberlain en 1955 en la Universidad de California, Berkeley . [1] Desde entonces, se han creado antipartículas de muchas otras partículas subatómicas en experimentos con aceleradores de partículas. En los últimos años, se han ensamblado átomos completos de antimateria a partir de antiprotones y positrones, recogidos en trampas electromagnéticas. [2]
... el desarrollo de la teoría cuántica de campos hizo innecesaria la interpretación de las antipartículas como agujeros, aunque persiste en muchos libros de texto.
Steven Weinberg [3]
Las soluciones de la ecuación de Dirac contienen estados cuánticos de energía negativa. Como resultado, un electrón siempre podría irradiar energía y caer en un estado de energía negativa. Peor aún, podría seguir irradiando cantidades infinitas de energía porque había infinitos estados de energía negativa disponibles. Para evitar que ocurriera esta situación no física, Dirac propuso que un "mar" de electrones de energía negativa llena el universo, ocupando ya todos los estados de energía más bajos de modo que, debido al principio de exclusión de Pauli , ningún otro electrón podría caer en ellos. Sin embargo, a veces, una de estas partículas de energía negativa podría ser extraída de este mar de Dirac para convertirse en una partícula de energía positiva. Pero, al ser extraída, dejaría atrás un agujero en el mar que actuaría exactamente como un electrón de energía positiva con una carga invertida. Estos agujeros fueron interpretados como "electrones de energía negativa" por Paul Dirac y erróneamente identificados con protones en su artículo de 1930 Una teoría de electrones y protones [4] Sin embargo, estos "electrones de energía negativa" resultaron ser positrones y no protones .
Esta imagen implicaba una carga negativa infinita para el universo, un problema del que Dirac era consciente. Dirac intentó argumentar que percibiríamos esto como el estado normal de carga cero. Otra dificultad era la diferencia de masas del electrón y el protón. Dirac intentó argumentar que esto se debía a las interacciones electromagnéticas con el mar, hasta que Hermann Weyl demostró que la teoría de los agujeros era completamente simétrica entre cargas negativas y positivas. Dirac también predijo una reacción
mi−
+
pag+
→
gamma
+
gamma
, donde un electrón y un protón se aniquilan para dar lugar a dos fotones. Sin embargo, Robert Oppenheimer e Igor Tamm demostraron que esto haría que la materia ordinaria desapareciera demasiado rápido. Un año después, en 1931, Dirac modificó su teoría y postuló el positrón , una nueva partícula de la misma masa que el electrón. El descubrimiento de esta partícula al año siguiente eliminó las dos últimas objeciones a su teoría.
Dentro de la teoría de Dirac, el problema de la carga infinita del universo sigue vigente. Algunos bosones también tienen antipartículas, pero como los bosones no obedecen al principio de exclusión de Pauli (sólo los fermiones lo hacen), la teoría de agujeros no funciona para ellos. Ahora hay una interpretación unificada de las antipartículas disponible en la teoría cuántica de campos , que resuelve ambos problemas al describir la antimateria como estados de energía negativos del mismo campo de materia subyacente, es decir, partículas que se mueven hacia atrás en el tiempo. [5]

Si una partícula y una antipartícula se encuentran en los estados cuánticos apropiados, entonces pueden aniquilarse entre sí y producir otras partículas. Reacciones como
mi−
+
mi+
→
gamma
gamma
(la aniquilación de dos fotones de un par electrón-positrón) son un ejemplo. La aniquilación de un solo fotón de un par electrón-positrón,
mi−
+
mi+
→
gamma
, no puede ocurrir en el espacio libre porque es imposible conservar energía y momento juntos en este proceso. Sin embargo, en el campo de Coulomb de un núcleo la invariancia traslacional se rompe y puede ocurrir la aniquilación de un solo fotón. [11] La reacción inversa (en el espacio libre, sin un núcleo atómico) también es imposible por esta razón. En la teoría cuántica de campos, este proceso solo se permite como un estado cuántico intermedio durante tiempos lo suficientemente cortos como para que la violación de la conservación de la energía pueda ser acomodada por el principio de incertidumbre . Esto abre el camino para la producción de pares virtuales o la aniquilación en la que un estado cuántico de una partícula puede fluctuar en un estado de dos partículas y viceversa. Estos procesos son importantes en el estado de vacío y la renormalización de una teoría cuántica de campos. También abre el camino para la mezcla de partículas neutrales a través de procesos como el que se muestra aquí, que es un ejemplo complicado de renormalización de masas .
Los estados cuánticos de una partícula y una antipartícula se intercambian mediante la aplicación combinada de conjugación de carga , paridad e inversión temporal . y son operadores lineales unitarios, es antilineal y antiunitario, . Si denota el estado cuántico de una partícula con momento y espín cuyo componente en la dirección z es , entonces se tiene
donde denota el estado conjugado de carga, es decir, la antipartícula. En particular, una partícula masiva y su antipartícula se transforman bajo la misma representación irreducible del grupo de Poincaré, lo que significa que la antipartícula tiene la misma masa y el mismo espín.
Si , y pueden definirse por separado en las partículas y antipartículas, entonces
donde el signo de proporcionalidad indica que podría haber una fase en el lado derecho.
Como anticonmutan con las cargas, la partícula y la antipartícula tienen cargas eléctricas opuestas q y -q.
Se puede intentar cuantificar un campo de electrones sin mezclar los operadores de aniquilación y creación escribiendo
donde usamos el símbolo k para denotar los números cuánticos p y σ de la sección anterior y el signo de la energía, E(k) , y a k denota los operadores de aniquilación correspondientes. Por supuesto, dado que estamos tratando con fermiones , tenemos que hacer que los operadores satisfagan las relaciones de anticonmutación canónicas. Sin embargo, si uno escribe ahora el hamiltoniano
Entonces se ve inmediatamente que el valor esperado de H no necesita ser positivo. Esto se debe a que E(k) puede tener cualquier signo y la combinación de operadores de creación y aniquilación tiene un valor esperado de 1 o 0.
Por lo tanto, hay que introducir el campo de antipartículas conjugado de carga , con sus propios operadores de creación y aniquilación que satisfagan las relaciones
donde k tiene la misma p y σ opuesta y el signo de la energía. Entonces se puede reescribir el campo en la forma
donde la primera suma es sobre los estados de energía positiva y la segunda sobre los de energía negativa. La energía se convierte en
donde E 0 es una constante negativa infinita. El estado de vacío se define como el estado sin partículas ni antipartículas, es decir , y . Entonces la energía del vacío es exactamente E 0 . Como todas las energías se miden en relación con el vacío, H es definida positiva. El análisis de las propiedades de a k y b k muestra que uno es el operador de aniquilación para partículas y el otro para antipartículas. Este es el caso de un fermión .
Este enfoque se debe a Vladimir Fock , Wendell Furry y Robert Oppenheimer . Si se cuantifica un campo escalar real , se descubre que solo hay un tipo de operador de aniquilación; por lo tanto, los campos escalares reales describen bosones neutros. Dado que los campos escalares complejos admiten dos tipos diferentes de operadores de aniquilación, que están relacionados por conjugación, dichos campos describen bosones cargados.
Al considerar la propagación de los modos de energía negativos del campo electrónico hacia atrás en el tiempo, Ernst Stückelberg llegó a una comprensión pictórica del hecho de que la partícula y la antipartícula tienen masa m y espín J iguales pero cargas opuestas q . Esto le permitió reescribir la teoría de perturbaciones con precisión en forma de diagramas. Richard Feynman más tarde dio una derivación sistemática independiente de estos diagramas a partir de un formalismo de partículas, y ahora se llaman diagramas de Feynman . Cada línea de un diagrama representa una partícula que se propaga hacia atrás o hacia adelante en el tiempo. En los diagramas de Feynman, las antipartículas se muestran viajando hacia atrás en el tiempo en relación con la materia normal, y viceversa. [12] Esta técnica es el método más extendido para calcular amplitudes en la teoría cuántica de campos en la actualidad.
Dado que esta imagen fue desarrollada por primera vez por Stückelberg, [13] y adquirió su forma moderna en el trabajo de Feynman, [14] se la llama interpretación de Feynman-Stückelberg de las antipartículas en honor a ambos científicos.