Identidad (matemáticas)

Ecuación que se satisface para todos los valores de las variables.

Prueba visual de la identidad pitagórica : para cualquier ángulo , el punto se encuentra en el círculo unitario , lo que satisface la ecuación . De este modo, . ${\displaystyle \theta }$ ${\displaystyle (x,y)=(\cos \theta ,\sin \theta )}$ ${\displaystyle x^{2}+y^{2}=1}$ ${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1}$

En matemáticas , una identidad es una igualdad que relaciona una expresión matemática A  con otra expresión matemática  B , de modo que A y B (que pueden contener algunas variables ) producen el mismo valor para todos los valores de las variables dentro de un cierto rango de validez. ^[1] En otras palabras, A  =  B es una identidad si A y B definen las mismas funciones , y una identidad es una igualdad entre funciones que están definidas de manera diferente. Por ejemplo, y son identidades. ^[1] Las identidades a veces se indican con el símbolo de barra triple ≡ en lugar de = , el signo igual . ^[2] Formalmente, una identidad es una igualdad universalmente cuantificada . ${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ ${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1}$

Identidades comunes

Identidades algebraicas

Ciertas identidades, como y , forman la base del álgebra , ^[3] mientras que otras identidades, como y , pueden ser útiles para simplificar expresiones algebraicas y expandirlas. ^[4] ${\displaystyle a+0=a}$ ${\displaystyle a+(-a)=0}$ ${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ ${\displaystyle a^{2}-b^{2}=(a+b)(a-b)}$

Identidades trigonométricas

Geométricamente, las identidades trigonométricas son identidades que involucran ciertas funciones de uno o más ángulos . ^[5] Son distintos de las identidades de triángulos , que son identidades que involucran tanto ángulos como longitudes de lados de un triángulo . En este artículo sólo se tratan los primeros.

Estas identidades son útiles cuando es necesario simplificar expresiones que involucran funciones trigonométricas. Otra aplicación importante es la integración de funciones no trigonométricas: una técnica común que implica usar primero la regla de sustitución con una función trigonométrica y luego simplificar la integral resultante con una identidad trigonométrica.

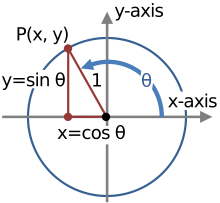
Uno de los ejemplos más destacados de identidades trigonométricas involucra la ecuación que es verdadera para todos los valores reales de . Por otra parte, la ecuación ${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1,}$ ${\displaystyle \theta }$

${\displaystyle \cos \theta =1}$

solo es cierto para ciertos valores de , no para todos. Por ejemplo, esta ecuación es verdadera cuando pero falsa cuando . ${\displaystyle \theta }$ ${\displaystyle \theta =0,}$ ${\displaystyle \theta =2}$

Otro grupo de identidades trigonométricas se refiere a las llamadas fórmulas de suma/resta (por ejemplo, la identidad de doble ángulo , la fórmula de suma para ), ^[2] que pueden usarse para descomponer expresiones de ángulos mayores en aquellos con constituyentes más pequeños. ${\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }$ ${\displaystyle \tan(x+y)}$

Identidades exponenciales

Las siguientes identidades son válidas para todos los exponentes enteros , siempre que la base sea distinta de cero:

${\displaystyle {\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}}$

A diferencia de la suma y la multiplicación, la exponenciación no es conmutativa . Por ejemplo, 2 + 3 = 3 + 2 = 5 y 2 · 3 = 3 · 2 = 6 , pero 2 ³ = 8 mientras que 3 ² = 9 .

Además, a diferencia de la suma y la multiplicación, la exponenciación tampoco es asociativa . Por ejemplo, (2 + 3) + 4 = 2 + (3 + 4) = 9 y (2 · 3) · 4 = 2 · (3 · 4) = 24 , pero 2 ³ elevado al 4 es 8 ⁴ (o 4.096) mientras que 2 elevado a 3 ⁴ es 2 ⁸¹ (o 2.417.851.639.229.258.349.412.352). Cuando no se escriben paréntesis, por convención el orden es de arriba hacia abajo, no de abajo hacia arriba:

${\displaystyle b^{p^{q}}:=b^{(p^{q})},}$   mientras   ${\displaystyle (b^{p})^{q}=b^{p\cdot q}.}$

Identidades logarítmicas

Varias fórmulas importantes, a veces llamadas identidades logarítmicas o leyes logarítmicas , relacionan los logaritmos entre sí: ^[a]

Producto, cociente, potencia y raíz.

El logaritmo de un producto es la suma de los logaritmos de los números que se multiplican; el logaritmo de la razón de dos números es la diferencia de los logaritmos. El logaritmo de la p -ésima potencia de un número es p multiplicado por el logaritmo del número mismo; el logaritmo de una raíz p -ésima es el logaritmo del número dividido por p . La siguiente tabla enumera estas identidades con ejemplos. Cada una de las identidades se puede derivar después de sustituir las definiciones de logaritmos y/o en el lado izquierdo. ${\displaystyle x=b^{\log _{b}x},}$ ${\displaystyle y=b^{\log _{b}y},}$

Cambio de base

El logaritmo log _b ( x ) se puede calcular a partir de los logaritmos de x y b con respecto a una base arbitraria k usando la siguiente fórmula:

${\displaystyle \log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.}$

Las calculadoras científicas típicas calculan los logaritmos en bases 10 y e . ^[6] Los logaritmos con respecto a cualquier base b se pueden determinar utilizando cualquiera de estos dos logaritmos mediante la fórmula anterior:

${\displaystyle \log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e}(x)}{\log _{e}(b)}}.}$

Dado un número x y su logaritmo log _b ( x ) con base desconocida b , la base viene dada por:

${\displaystyle b=x^{\frac {1}{\log _{b}(x)}}.}$

Identidades de funciones hiperbólicas

Las funciones hiperbólicas satisfacen muchas identidades, todas ellas similares en forma a las identidades trigonométricas . De hecho, la regla de Osborn ^[7] establece que se puede convertir cualquier identidad trigonométrica en una identidad hiperbólica expandiéndola completamente en términos de potencias enteras de senos y cosenos, cambiando seno a sinh y coseno a cosh, y cambiando el signo de cada término. que contiene un producto de un número par de senos hiperbólicos. ^[8]

La función Gudermanniana da una relación directa entre las funciones trigonométricas y las hiperbólicas que no involucra números complejos .

Lógica y álgebra universal.

Formalmente, una identidad es una verdadera fórmula universalmente cuantificada de la forma donde s y t son términos sin otras variables libres que el prefijo cuantificador a menudo se deja implícito cuando se afirma que la fórmula es una identidad. Por ejemplo, los axiomas de un monoide a menudo se dan como fórmulas ${\displaystyle \forall x_{1},\ldots ,x_{n}:s=t,}$ ${\displaystyle x_{1},\ldots ,x_{n}.}$ ${\displaystyle \forall x_{1},\ldots ,x_{n}}$

${\displaystyle \forall x,y,z:x*(y*z)=(x*y)*z,\quad \forall x:x*1=x,\quad \forall x:1*x=x,}$

o, en breve,

${\displaystyle x*(y*z)=(x*y)*z,\qquad x*1=x,\qquad 1*x=x.}$

Entonces, estas fórmulas son identidades en cada monoide. Como ocurre con cualquier igualdad, las fórmulas sin cuantificador suelen denominarse ecuaciones . En otras palabras, una identidad es una ecuación que es verdadera para todos los valores de las variables. ^{[9] [10]}

Ver también

• Identidad contable
• Lista de identidades matemáticas

Referencias

Notas

1. Todas las declaraciones de esta sección se pueden encontrar en Shirali 2002, Sección 4, Downing 2003, p. 275, o Kate y Bhapkar 2009, pág. 1-1, por ejemplo.

Citas

1. "Palabras matemáticas: identidad". www.mathwords.com . Consultado el 1 de diciembre de 2019 .
2. "Identidad - definición de palabras matemáticas - Referencia abierta de matemáticas". www.mathopenref.com . Consultado el 1 de diciembre de 2019 .
3. "Identidades básicas". www.matemáticas.com . Consultado el 1 de diciembre de 2019 .
4. "Identidades algebraicas". www.sosmath.com . Consultado el 1 de diciembre de 2019 .
5. Stapel, Isabel. "Identidades trigonométricas". Matemáticas moradas . Consultado el 1 de diciembre de 2019 .
6. Bernstein, Stephen; Bernstein, Ruth (1999), Esquema de la teoría y los problemas de los elementos de la estadística de Schaum. I, Estadística descriptiva y probabilidad , serie de esquemas de Schaum, Nueva York: McGraw-Hill , ISBN 978-0-07-005023-5, pag. 21
7. Osborn, G. (1 de enero de 1902). "109. Mnemónico para fórmulas hiperbólicas". La Gaceta Matemática . 2 (34): 189. doi : 10.2307/3602492. JSTOR  3602492.
8. Peterson, John Charles (2003). Matemáticas técnicas con cálculo (3ª ed.). Aprendizaje Cengage. pag. 1155.ISBN​ 0-7668-6189-9., Capítulo 26, página 1155
9. Nachum Dershowitz ; Jean-Pierre Jouannaud (1990). "Reescribir sistemas". En Jan van Leeuwen (ed.). Modelos formales y semántica . Manual de informática teórica. vol. B. Elsevier. págs. 243–320.
10. Wolfgang Wechsler (1992). Wilfried Brauer ; Grzegorz Rozenberg ; Arto Salomaa (eds.). Álgebra universal para informáticos . Monografías de la EATCS sobre informática teórica. vol. 25. Berlín: Springer. ISBN 3-540-54280-9.Aquí: Def.1 del Apartado 3.2.1, p.160.

Fuentes

• Downing, Douglas (2003). Álgebra de forma fácil. Serie educativa Barrons. ISBN 978-0-7641-1972-9.
• Kate, SK; Bhapkar, recursos humanos (2009). Conceptos básicos de matemáticas. Publicaciones técnicas. ISBN 978-81-8431-755-8.
• Shirali, S. (2002). Aventuras en la resolución de problemas. Prensa Universitaria. ISBN 978-81-7371-413-9.

enlaces externos

• La Enciclopedia de Ecuaciones Enciclopedia en línea de identidades matemáticas (archivada)
• Una colección de identidades algebraicas