La holografía generada por computadora ( CGH ) es una técnica que utiliza algoritmos informáticos para generar hologramas . Implica la generación de patrones de interferencia holográfica . Un holograma generado por computadora se puede mostrar en una pantalla holográfica dinámica o se puede imprimir en una máscara o película mediante litografía. [1] Cuando se imprime un holograma en una máscara o película, luego se ilumina con una fuente de luz coherente para mostrar las imágenes holográficas.
El término "holografía generada por computadora" se ha utilizado para designar toda la cadena de procesos de preparación sintética de frentes de onda de luz holográficos adecuados para la observación. [2] [3] Si los datos holográficos de objetos existentes se generan ópticamente y se registran y procesan digitalmente, y luego se muestran, esto también se denomina CGH.
En comparación con los hologramas clásicos, los hologramas generados por ordenador tienen la ventaja de que los objetos que se quieren mostrar no tienen por qué poseer ninguna realidad física y pueden ser generados de forma completamente sintética.
En última instancia, la holografía generada por computadora podría ampliar todas las funciones de las imágenes generadas por computadora actuales. Las pantallas holográficas de computadora podrían usarse para una amplia gama de aplicaciones, por ejemplo, diseño asistido por computadora (CAD), juegos y video holográfico.
La holografía es una técnica inventada originalmente por el físico húngaro Dennis Gabor (1900-1979) para mejorar el poder de resolución de los microscopios electrónicos. Se ilumina un objeto con un haz de luz coherente (normalmente monocromático); la luz dispersa se lleva a interferencia con un haz de referencia de la misma fuente, registrando el patrón de interferencia. La CGH, tal como se define en la introducción, tiene tres funciones generales:
Hay que tener en cuenta que no siempre está justificado hacer una distinción estricta entre estos pasos; sin embargo, resulta útil estructurar la discusión de esta manera.
Los hologramas generados por ordenador ofrecen importantes ventajas con respecto a los hologramas ópticos, ya que no se necesita un objeto real. Debido a este avance, se esperaba una visualización tridimensional cuando se informaron los primeros algoritmos en 1966. [4]
Desafortunadamente, los investigadores pronto se dieron cuenta de que hay límites inferiores y superiores notables en términos de velocidad computacional y calidad y fidelidad de imagen respectivamente. Los cálculos de frente de onda son computacionalmente muy intensivos; incluso con técnicas matemáticas modernas y equipos informáticos de alta gama, el cálculo en tiempo real es complicado. Hay muchos métodos diferentes para calcular el patrón de interferencia para un CGH. En los siguientes 25 años, se propusieron muchos métodos para hologramas generados por computadora en los campos de la información holográfica y la reducción computacional, así como en técnicas computacionales y de cuantificación. [5] [6] [7] [8] [9] [10] [11] Los algoritmos se pueden clasificar en dos conceptos principales: hologramas de transformada de Fourier y hologramas de fuente puntual.
Uno de los métodos más comunes que se pueden utilizar para generar hologramas de solo fase es el algoritmo Gerchberg-Saxton (GS) . [12] [13]
En el primero, se utiliza la transformación de Fourier para simular la propagación de cada plano de profundidad del objeto al plano del holograma. El concepto de transformación de Fourier fue introducido por primera vez por Byron R. Brown y Adolf W. Lohmann [4] con el método de fase de desvío que conduce a hologramas orientados a celdas. Una técnica de codificación sugerida por Burch [14] reemplazó los hologramas orientados a celdas por hologramas puntuales e hizo que este tipo de hologramas generados por computadora fueran más atractivos. En un holograma de transformada de Fourier, la reconstrucción de la imagen ocurre en el campo lejano . Esto generalmente se logra utilizando las propiedades de transformación de Fourier de una lente positiva para la reconstrucción. Entonces, hay dos pasos en este proceso: calcular el campo de luz en el plano del observador lejano y luego transformar este campo de Fourier nuevamente al plano de la lente. Estos hologramas se denominan hologramas basados en Fourier. Los primeros CGH basados en la transformada de Fourier podían reconstruir solo imágenes 2D. Brown y Lohmann [15] introdujeron una técnica para calcular hologramas generados por ordenador de objetos 3D. El cálculo de la propagación de la luz a partir de objetos tridimensionales se realiza según la aproximación parabólica habitual a la integral de difracción de Fresnel-Kirchhoff. El frente de onda que se va a reconstruir mediante el holograma es, por tanto, la superposición de las transformadas de Fourier de cada plano del objeto en profundidad, modificadas por un factor de fase cuadrático.
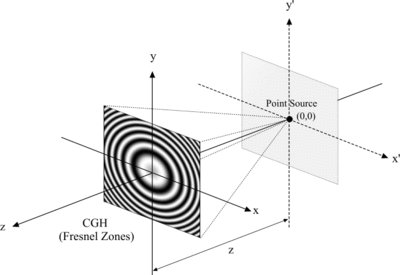
La segunda estrategia computacional se basa en el concepto de fuente puntual, donde el objeto se descompone en puntos autoluminosos. Se calcula un holograma elemental para cada fuente puntual y el holograma final se sintetiza superponiendo todos los hologramas elementales. Este concepto fue reportado por primera vez por Waters [16], cuyo supuesto principal se originó con Rogers [17], quien reconoció que una placa de zona de Fresnel podría considerarse un caso especial del holograma propuesto por Gabor. Pero, en la medida en que la mayoría de los puntos del objeto eran distintos de cero, la complejidad computacional del concepto de fuente puntual era mucho mayor que en el concepto de transformación de Fourier. Algunos investigadores intentaron superar este inconveniente predefiniendo y almacenando todos los hologramas elementales posibles utilizando técnicas especiales de almacenamiento de datos [18] debido a la gran capacidad que se necesita en este caso, otros utilizando hardware especial. [19]
En el concepto de fuente puntual, el problema principal es el equilibrio entre la capacidad de almacenamiento de datos y la velocidad computacional. En particular, los algoritmos que aumentan la velocidad computacional suelen tener requisitos de almacenamiento de datos mucho mayores [18], mientras que los algoritmos que reducen los requisitos de almacenamiento de datos tienen una alta complejidad computacional [20] [21] [22] (aunque son posibles algunas optimizaciones [23] ).
Otro concepto que conduce a los CGH de fuente puntual es el método de trazado de rayos . El trazado de rayos es quizás el método más simple de visualización de holografía generada por computadora. Básicamente, se calcula la diferencia de longitud de trayectoria entre la distancia que deben recorrer un "haz de referencia" virtual y un "haz de objeto" virtual; esto dará la fase relativa del haz de objeto disperso.
En las últimas tres décadas, ambos conceptos han avanzado notablemente en la mejora de la velocidad computacional y la calidad de las imágenes. Sin embargo, algunas limitaciones técnicas, como la capacidad de cómputo y de almacenamiento, siguen siendo una carga para la holografía digital, lo que hace que las aplicaciones en tiempo real sean casi imposibles con el hardware informático estándar actual.
Una vez que se conoce cómo se ve el frente de onda disperso del objeto o cómo se puede calcular, se debe fijar en un modulador espacial de luz (SLM), abusando de este término para incluir no solo pantallas LCD o dispositivos similares, sino también películas y máscaras. Básicamente, existen diferentes tipos de SLM disponibles: moduladores de fase pura (que retardan la onda de iluminación), moduladores de amplitud pura (que bloquean la luz de iluminación), moduladores de polarización (que influyen en el estado de polarización de la luz) [24] y SLM que tienen la capacidad de modulación combinada de fase/amplitud. [25]
En el caso de la modulación de amplitud o fase pura, es evidente que las pérdidas de calidad son inevitables. Las primeras formas de hologramas de amplitud pura se imprimían simplemente en blanco y negro, lo que significa que la amplitud tenía que codificarse con un solo bit de profundidad. [4] De manera similar, la kinoforma es una codificación de fase pura inventada en IBM en los primeros días de CGH. [26]
Aunque una modulación de fase/amplitud completamente compleja sería ideal, normalmente se prefiere una solución de fase pura o de amplitud pura porque es mucho más fácil de implementar tecnológicamente. Sin embargo, para la creación de una distribución de luz complicada, la modulación simultánea de amplitud y fase es razonable. Hasta ahora se han implementado dos enfoques diferentes para la modulación de amplitud-fase. Uno se basa en la modulación de fase solamente o de amplitud solamente y el filtrado espacial consecutivo, [27] el otro se basa en hologramas de polarización con orientación variable y magnitud de birrefringencia local. [28] Los hologramas con una restricción, como fase solamente o amplitud solamente, se pueden calcular mediante algoritmos como el algoritmo de Gerchberg-Saxton o algoritmos de optimización más generales como la búsqueda directa, el recocido simulado [29] o el descenso de gradiente estocástico utilizando, por ejemplo, TensorFlow. [30]
El tercer problema (técnico) es la modulación del haz y la reconstrucción del frente de onda. Se pueden imprimir máscaras, lo que a menudo da como resultado una estructura de patrón granulado, ya que la mayoría de las impresoras solo pueden hacer puntos (aunque muy pequeños). Las películas se pueden revelar mediante exposición láser . Las pantallas holográficas siguen siendo un desafío en la actualidad (a fecha de 2008 [actualizar]), aunque se han construido prototipos exitosos. Una pantalla ideal para hologramas generados por computadora consistiría en píxeles más pequeños que una longitud de onda de luz con fase y brillo ajustables. Estas pantallas se han llamado óptica de matriz en fase . [31] Se requieren más avances en nanotecnología para construirlas.
Actualmente, varias empresas y departamentos universitarios están investigando en el campo de los dispositivos CGH:
Recientemente, la holografía generada por ordenador se ha extendido en su uso más allá de la óptica de la luz y se ha aplicado en la generación de funciones de onda electrónicas estructuradas con una amplitud y un perfil de fase deseados. Los hologramas generados por ordenador se diseñan mediante la interferencia de una onda objetivo con una onda de referencia, que podría ser, por ejemplo, una onda plana ligeramente inclinada en una dirección. Los elementos ópticos difractivos holográficos utilizados suelen estar construidos a partir de membranas delgadas de materiales como el nitruro de silicio.