Alta generación de armónicos

Proceso científico del láser

La generación de armónicos altos ( HHG ) es un proceso no lineal durante el cual un objetivo (muestra de gas, plasma, sólida o líquida) se ilumina con un pulso láser intenso. En tales condiciones, la muestra emitirá los armónicos altos del haz de generación (por encima del quinto armónico). Debido a la naturaleza coherente del proceso, la generación de armónicos altos es un requisito previo de la física de attosegundos .

Generación de armónicos perturbativos

La generación de armónicos perturbativos es un proceso mediante el cual se puede utilizar luz láser de frecuencia ω y energía fotónica ħω para generar nuevas frecuencias de luz. Las frecuencias recién generadas son múltiplos enteros nω de la frecuencia de la luz original. Este proceso fue descubierto por primera vez en 1961 por Franken et al., ^[1] utilizando un láser de rubí , con cuarzo cristalino como medio no lineal .

La generación de armónicos en sólidos dieléctricos es bien conocida y ampliamente utilizada en la física láser moderna (ver generación de segundo armónico ). En 1967, New et al. observaron la primera generación de tercer armónico en un gas. ^[2] En gases monoatómicos solo es posible producir armónicos impares por razones de simetría. La generación de armónicos en el régimen perturbativo (campo débil) se caracteriza por una eficiencia que disminuye rápidamente con el aumento del orden armónico. ^[3] Este comportamiento se puede entender considerando un átomo que absorbe n fotones y luego emite un solo fotón de alta energía. La probabilidad de absorber n fotones disminuye a medida que n aumenta, lo que explica la rápida disminución de las intensidades armónicas iniciales.

Desarrollo

Espectro de una fuente de HHG de neón impulsada por un láser de zafiro Ti

La primera generación de armónicos altos se observó en 1977 en la interacción de pulsos láser de CO2 intensos con _plasma generado a partir de objetivos sólidos. ^[4] La generación de HHG en gases, mucho más extendida en aplicación hoy en día, fue observada por primera vez por McPherson y colegas en 1987, ^[5] y más tarde por Ferray et al. en 1988, ^[6] con resultados sorprendentes: se encontró que los armónicos altos disminuían en intensidad en órdenes bajos, como se esperaba, pero luego se observó que formaban una meseta, con la intensidad de los armónicos permaneciendo aproximadamente constante durante muchos órdenes. ^[7] Se han medido armónicos de meseta que abarcan cientos de eV que se extienden hasta el régimen de rayos X suaves . ^[8] Esta meseta termina abruptamente en una posición llamada el corte de armónicos altos.

Propiedades

Los armónicos altos tienen varias propiedades interesantes. Son una fuente de rayos X suaves/ XUV ajustable , sincronizada con el láser de accionamiento y producida con la misma tasa de repetición. El límite armónico varía linealmente con el aumento de la intensidad del láser hasta la intensidad de saturación I _sat , donde se detiene la generación de armónicos. ^[9] La intensidad de saturación se puede aumentar cambiando las especies atómicas a gases nobles más ligeros , pero estos tienen una menor eficiencia de conversión, por lo que se debe encontrar un equilibrio dependiendo de las energías de los fotones requeridas.

La generación de armónicos altos depende en gran medida del campo láser de accionamiento y, como resultado, los armónicos tienen propiedades de coherencia temporal y espacial similares. ^[10] Los armónicos altos a menudo se generan con duraciones de pulso más cortas que las del láser de accionamiento. ^[11] Esto se debe a la no linealidad del proceso de generación, la coincidencia de fases y la ionización . A menudo, los armónicos solo se producen en una ventana temporal muy pequeña cuando se cumple la condición de coincidencia de fases. El agotamiento del medio generador debido a la ionización también significa que la generación de armónicos se limita principalmente al borde delantero del pulso de accionamiento. ^[12]

Los armónicos altos se emiten de forma colineal con el láser de accionamiento y pueden tener un confinamiento angular muy estrecho, a veces con menos divergencia que la del campo fundamental y perfiles de haz cercanos a los gaussianos. ^[13]

Enfoque semiclásico

La máxima energía fotónica que se puede producir con una generación de armónicos alta viene dada por el límite de corte de la meseta armónica. Esto se puede calcular de forma clásica examinando la energía máxima que el electrón ionizado puede ganar en el campo eléctrico del láser. La energía de corte viene dada por: ^[14]

${\displaystyle E_{\mathrm {max} }=I_{p}+3.17\ U_{p}}$

donde U _p es la energía ponderomotriz del campo láser e I _p es el potencial de ionización .

Esta energía de corte se deriva de un cálculo semiclásico, a menudo llamado modelo de tres pasos. El electrón se trata inicialmente de manera mecanocuántica a medida que se ioniza por efecto túnel desde el átomo original, pero su dinámica posterior se trata de manera clásica. Se supone que el electrón nace en el vacío con una velocidad inicial cero y que posteriormente es acelerado por el campo eléctrico del rayo láser .

El modelo de tres pasos

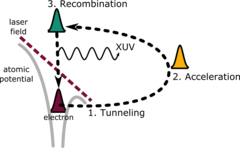
Después de medio ciclo óptico de ionización, el electrón invertirá su dirección a medida que el campo eléctrico cambia de signo y acelerará de nuevo hacia el núcleo original. Al regresar al núcleo original, puede emitir radiación similar a la radiación de frenado durante un proceso de recombinación con el átomo cuando vuelve a su estado fundamental . Esta descripción se conoce como el modelo de recolisión de generación de armónicos altos. ^[15]

Energía de retorno del electrón (curva azul completa) y tiempo de excursión (curva discontinua azul), en función del tiempo de retorno

Como la frecuencia de la radiación emitida depende tanto de la energía cinética como del potencial de ionización, las diferentes frecuencias se emiten en diferentes tiempos de recombinación (es decir, el pulso emitido se llama chirrido ). Además, para cada frecuencia, hay dos tiempos de recombinación correspondientes. Nos referimos a estas dos trayectorias como la trayectoria corta (que se emite primero) y la trayectoria larga.

En la imagen semiclásica, la HHG solo se producirá si el campo láser impulsor está polarizado linealmente. La elipticidad del haz láser hace que el electrón que regresa no toque el núcleo original. Desde el punto de vista de la mecánica cuántica, se reduce la superposición del paquete de ondas del electrón que regresa con el paquete de ondas nuclear. Esto se ha observado experimentalmente, donde la intensidad de los armónicos disminuye rápidamente al aumentar la elipticidad. ^[16] Otro efecto que limita la intensidad del láser impulsor es la fuerza de Lorentz . A intensidades superiores a 10 ¹⁶ W·cm ⁻² , el componente magnético del pulso láser, que se ignora en la óptica de campo débil, puede llegar a ser lo suficientemente fuerte como para desviar el electrón que regresa. Esto hará que "no toque" el núcleo original y, por tanto, impida la HHG.

Coincidencia de fases

Como en todo proceso no lineal , la coincidencia de fases desempeña un papel importante en la generación de armónicos elevados en la fase gaseosa. En la geometría de enfoque libre, las cuatro causas de la falta de coincidencia de vectores de onda son: dispersión neutra, dispersión de plasma, fase de Gouy y fase dipolar. ^{[17] [18]}

La dispersión neutra es causada por los átomos mientras que la dispersión de plasma es debida a los iones, y las dos tienen signos opuestos. La fase de Gouy es debida al salto de fase del frente de onda cerca del foco, y varía a lo largo de él. Finalmente, la fase dipolar surge de la respuesta atómica en el proceso HHG. ^[19] Cuando se utiliza una geometría de chorro de gas, las condiciones óptimas para generar armónicos altos emitidos desde trayectorias cortas se obtienen cuando el gas generador se ubica después del foco, mientras que la generación de armónicos altos desde trayectorias largas se puede obtener fuera del eje cuando el gas generador se ubica antes del foco. ^[20]

Además, la implementación de una geometría de enfoque flexible para el campo de conducción permite que una mayor cantidad de emisores y fotones contribuyan al proceso de generación y, por lo tanto, mejoren el rendimiento armónico. ^[21] Cuando se utiliza una geometría de chorro de gas, enfocar el láser en el disco de Mach puede aumentar la eficiencia de la generación de armónicos. ^[22]

De manera más general, en la región espectral de rayos X, los materiales tienen un índice de refracción muy cercano a 1. Para equilibrar el desajuste de fase, necesitamos encontrar dichos parámetros en el espacio de alta dimensión que efectivamente harán que el índice de refracción combinado en la longitud de onda del láser impulsor sea casi 1. ${\displaystyle \Delta k=k_{q}-qk_{L}}$

Para lograr niveles de intensidad que puedan distorsionar el potencial de enlace de un átomo, es necesario enfocar el haz láser impulsor. Esto introduce términos de dispersión que afectan el desajuste de fase, dependiendo de la geometría específica (como propagación de onda plana, enfoque libre, guía de onda de núcleo hueco, etc.). Además, durante el proceso de generación de armónicos altos, los electrones se aceleran y algunos de ellos regresan a su ion original, lo que da como resultado ráfagas de rayos X. Sin embargo, la mayoría de estos electrones no regresan y, en cambio, contribuyen a la dispersión de las ondas que se propagan conjuntamente. Los electrones que regresan transportan fase debido a procesos como ionización, recombinación y propagación. Además, los átomos ionizados pueden influir en el índice de refracción del medio, lo que proporciona otra fuente de dispersión.

El desajuste de fase (>0 la velocidad de fase del láser es más rápida que la de los rayos X) se puede representar como:

${\displaystyle \Delta k=k_{q}-qk_{L}=\underbrace {\Delta k_{\mathrm {neutrals} }} _{<0}+\underbrace {\Delta k_{\mathrm {ions} }} _{<0}+\underbrace {\Delta k_{\mathrm {electrons} }} _{>0}+\underbrace {\Delta k_{\mathrm {geometry} }} _{>0}+\underbrace {\Delta k_{\mathrm {intrinsic} }} _{>\;\!0}+\cdots }$

donde es la contribución de los átomos neutros, es la contribución de los iones (cuando los neutros están ionizados, este término puede ser todavía suficientemente grande en el UV ^[23] ), es la contribución del plasma, es la geometría de enfoque libre, la geometría de guía de onda de onda plana, es la fase acumulada por el electrón durante el tiempo que pasa alejado del átomo, etc. Cada término tiene un signo específico que permite equilibrar el desajuste en un tiempo y frecuencia particulares. ${\displaystyle \Delta k_{\mathrm {neutrals} }}$ ${\displaystyle \Delta k_{\mathrm {ions} }}$ ${\displaystyle \Delta k_{\mathrm {electrons} }}$ ${\displaystyle \Delta k_{\mathrm {geometry} }}$ ${\displaystyle \Delta k_{\mathrm {intrinsic} }}$

La contribución de los electrones escala cuadráticamente con la longitud de onda: , mientras que la contribución de los átomos escala inversamente con la longitud de onda: . Por lo tanto, en longitudes de onda IR largas, el término es bastante grande por electrón, mientras que el término es bastante pequeño y cercano a uno. Para igualar la fase del proceso de HHG, se requieren presiones muy altas y niveles bajos de ionización, lo que da como resultado una gran cantidad de emisores. ^[24] En el rango espectral UV opuesto, el término es grande debido a las resonancias UV ubicadas cerca y, además, el término es pequeño. Para igualar la fase del proceso, se necesitan bajas presiones. Además, en el UV, se pueden tolerar niveles de ionización muy altos (mucho mayores que 100%). Esto le da a HHG escalabilidad de energía de fotones con la intensidad del láser UV impulsor. ^[23] La geometría de onda simple o geometría de enfoque suelto permite una coincidencia de fase altamente colineal y una extracción de flujo máxima en las longitudes de onda impulsoras donde el término es pequeño. La generación de armónicos de alto orden en la guía de ondas permite una propagación con características cercanas a las de la propagación de ondas planas. ^[25] Estas geometrías son beneficiosas, especialmente los espectros de rayos X generados por rayos IR, donde se necesitan volúmenes de interacción largos para una extracción óptima de potencia. En estas geometrías, se han generado espectros que se extienden hasta 1,6 keV. ^[24] Para los armónicos altos impulsados ​​por UV-VIS, el término de la guía de ondas es pequeño y la imagen de coincidencia de fase se asemeja a la geometría de onda plana. En estas geometrías, se han generado armónicos de ancho de banda estrecho que se extienden hasta el borde del carbono (300 eV). ^[23] ${\displaystyle \Delta n_{\mathrm {electrons} }\sim -\lambda ^{2}}$ ${\displaystyle \Delta n_{\mathrm {atoms} }\sim 1/\lambda ^{2}}$ ${\displaystyle \left|\Delta n_{\mathrm {electrons} }\right|}$ ${\displaystyle \Delta n_{\mathrm {atoms} }}$ ${\displaystyle \Delta n_{\mathrm {atoms} }}$ ${\displaystyle \left|\Delta n_{\mathrm {electrons} }\right|}$ ${\displaystyle {\vec {v}}\times {\vec {B}}}$

Véase también

• Física de attosegundos
• Óptica no lineal
• Fotoionización
• Generación resonante de altos armónicos a partir de columnas de plasma extirpadas por láser

Referencias

1. PA Franken, AE Hill, CW Peters y G. Weinreich, Phys. Rev. Lett. 7, 118 (1961).
2. Nuevo, GHC; Ward, JF (1967). "Generación óptica de tercer armónico en gases". Phys. Rev. Lett . 19 (10): 556–559. Código Bibliográfico :1967PhRvL..19..556N. doi :10.1103/physrevlett.19.556.
3. J. Wildenauer, Revista de Física Aplicada 62, 41 (1987).
4. Burnett, NH; et al. (1977). "Generación de armónicos en la interacción del láser de CO2 con el objetivo". Appl. Phys. Lett . 31 (3): 172–174. Código Bibliográfico :1977ApPhL..31..172B. doi :10.1063/1.89628.
5. McPherson, A.; et al. (1987). "Estudios de producción multifotónica de radiación ultravioleta de vacío en gases raros". JOSA B . 4 (4): 595. Bibcode :1987JOSAB...4..595M. doi :10.1364/JOSAB.4.000595.
6. Ferray, M.; et al. (1988). "Conversión de múltiples armónicos de la radiación de 1064 nm en gases raros". Journal of Physics B: Atomic, Molecular and Optical Physics . 21 (3): L31. Bibcode :1988JPhB...21L..31F. doi :10.1088/0953-4075/21/3/001. S2CID  250827054.
7. Li, XF; L'Huillier, A.; Ferray, M.; Lompre, LA; Mainfray, G. (1989). "Generación de múltiples armónicos en gases raros a alta intensidad láser". Physical Review A . 39 (11): 5751–5761. Bibcode :1989PhRvA..39.5751L. doi :10.1103/physreva.39.5751. PMID  9901157.
8. Seres, J.; et al. (2005). "Tecnología láser: fuente de rayos X coherentes de kiloelectronvoltios". Nature . 433 (7026): 596. Bibcode :2005Natur.433..596S. doi : 10.1038/433596a . PMID  15703738. S2CID  4425428.
9. Brabec, T.; Krausz, F. (2000). "Campos láser intensos de pocos ciclos: fronteras de la óptica no lineal". Reseñas de Física Moderna . 72 (2): 545–591. Bibcode :2000RvMP...72..545B. doi :10.1103/revmodphys.72.545.
10. L'Huillier, A.; Schafer, KJ; Kulander, KC (1991). "Aspectos teóricos de la generación de armónicos de campo intenso". Journal of Physics B: Atomic, Molecular and Optical Physics . 24 (15): 3315–3341. Bibcode :1991JPhB...24.3315L. doi :10.1088/0953-4075/24/15/004. S2CID  250751106.
11. Rayos X suaves de 43 attosegundos generados por un infrarrojo medio pasivamente estable con CEP, https://doi.org/10.1364/OE.25.027506
12. Schafer, KJ; Kulander, KC (1997). "Generación de altos armónicos a partir de láseres de bombeo ultrarrápidos". Physical Review Letters . 78 (4): 638–641. Código Bibliográfico :1997PhRvL..78..638S. doi :10.1103/physrevlett.78.638.
13. Tisch, JWG; et al. (1994). "Generación de armónicos de alto orden con resolución angular en helio". Physical Review A . 49 (1): R28–R31. Bibcode :1994PhRvA..49...28T. doi :10.1103/physreva.49.r28. PMID  9910285.
14. Krause, Jeffrey L.; Schafer, Kenneth J.; Kulander, Kenneth C. (1992). "Generación de armónicos de alto orden a partir de átomos e iones en el régimen de alta intensidad". Physical Review Letters . 68 (24): 3535–3538. Bibcode :1992PhRvL..68.3535K. doi :10.1103/PhysRevLett.68.3535. PMID  10045729.
15. Corkum, PB (1993). "Perspectiva plasmática sobre la ionización multifotónica de campo fuerte". Physical Review Letters . 71 (13): 1994–1997. Bibcode :1993PhRvL..71.1994C. doi :10.1103/physrevlett.71.1994. PMID  10054556. S2CID  29947935.
16. Dietrich, P.; Burnett, NH; Ivanov, M.; Corkum, PB (1994). "Generación de armónicos elevados e ionización multifotónica de dos electrones correlacionada con luz polarizada elípticamente". Physical Review A . 50 (5): R3585–R3588. Bibcode :1994PhRvA..50.3585D. doi :10.1103/physreva.50.r3585. PMID  9911439.
17. Altucci, C.; Starczewski, T.; Mevel, E.; Wahlström, C.-G.; Carré, B.; L'Huillier, A. (1996). "Influencia de la densidad atómica en la generación de armónicos de alto orden". J. Opt. Soc. Am. B . 13 (1): 148–156. Código Bibliográfico :1996JOSAB..13..148A. doi :10.1364/JOSAB.13.000148.
18. Pascal, Salieres; L'Huillier, Anne; Lewenstein, Maciej (1995). "Control de coherencia de armónicos de orden superior" (PDF) . Physical Review Letters . 74 (19): 3776–3779. Bibcode :1995PhRvL..74.3776S. doi :10.1103/physrevlett.74.3776. PMID  10058294. S2CID  35091499.
19. Lewenstein, Maciej; Salieres, Pascal; L'huillier, Anne (1995). "Fase de la polarización atómica en la generación de armónicos de orden superior". Physical Review A . 52 (6): 4747–4754. Bibcode :1995PhRvA..52.4747L. doi :10.1103/physreva.52.4747. PMID  9912816.
20. Balcou, Philippe; Salieres, Pascal; L'Huillier, Anne; Lewenstein, Maciej (1997). "Condiciones generalizadas de coincidencia de fase para armónicos altos: el papel de las fuerzas de gradiente de campo". Physical Review A . 55 (4): 3204–3210. Bibcode :1997PhRvA..55.3204B. doi :10.1103/PhysRevA.55.3204.
21. Takahashi, E.; Nabekawa, Y.; Midorikawa, K. (2002). "Generación de luz ultravioleta extrema coherente de 10 uj mediante el uso de armónicos de alto orden". Optics Letters . 27 (21): 1920–1922. Bibcode :2002OptL...27.1920T. doi :10.1364/OL.27.001920. PMID  18033402.
22. Grant-Jacob, James; Mills, Ben; Butcher, Tom; Chapman, Richard; Brocklesby, William; Frey, Jeremy (2011). "Influencia de la estructura del chorro de gas en la generación de armónicos altos" (PDF) . Optics Express . 19 (10): 9801–9806. Bibcode :2011OExpr..19.9801G. doi : 10.1364/OE.19.009801 . PMID  21643236.
23. Popmintchev, D.; Hernández-García, C.; Dollar, F.; Mancuso, CA; Peng, P.-C.; Barwick, B.; Gorman, TT; Alonso-Mori, R.; Ališauskas, S.; Andriukaitis, G.; Baltuška, A.; Bostedt, C.; Chen, M.-C.; Dakovski, GL; Durfee, CG; Eckert, S.; Fan, T.-M.; Ferguson, WR; Frischkorn, CG; et al. (2015). "Sorpresa ultravioleta: Generación eficiente de rayos X suaves de alto armónico en plasmas ionizados múltiples". Science . 350 (6265): 1225–1231. Código Bibliográfico :2015Sci...350.1225P. doi :10.1126/science.aac9755. hdl : 10366/147088 . PMID:  26785483. S2CID  : 2342988.
24. Popmintchev, T.; Chen, M.-C.; Popmintchev, D.; Arpin, P.; Marrón, S.; Alisauskas, S.; Andriukaitis, G.; Balciunas, T.; Mücke, OD; Pugzlys, A.; Baltuska, A.; Calza, B.; Schrauth, SE; Gaeta, A.; Hernández-García, C.; Plaja, L.; Becker, A.; Jaron-Becker, A.; Murnane, MM; et al. (2012). "Armónicos ultraaltos coherentes brillantes en el régimen de rayos X keV de láseres de femtosegundo del infrarrojo medio". Ciencia . 336 (6086): 1287–1291. arXiv : 2403.19535 . Código Bibliográfico :2012Sci...336.1287P. doi :10.1126/science.1218497. hdl : 10366/147089 . PMID  22679093. S2CID  24628513.
25. Rundquist, A.; Durfee, CG; Chang, Z.; Herne, C.; Backus, S.; Murnane, MM; Kapteyn, HC (1998). "Generación de rayos X suaves coherentes con ajuste de fase". Science . 280 (5368): 1412–1415. arXiv : 2403.19636 . Bibcode :1998Sci...280.1412R. doi :10.1126/science.280.5368.1412. PMID  9603725.