Heptágono

Figura con siete lados

En geometría , un heptágono o septágono es un polígono de siete lados o 7-gono.

Al heptágono se lo denomina a veces septágono , utilizando "sept-" (una elisión de septua- , un prefijo numérico derivado del latín , en lugar de hepta- , un prefijo numérico derivado del griego ; ambos son afines) junto con el sufijo griego "-agon", que significa ángulo.

Heptágono regular

Un heptágono regular , en el que todos los lados y todos los ángulos son iguales, tiene ángulos internos de 5π/7 radianes (128 4 ⁄ 7 grados ). Su símbolo de Schläfli es {7}.

Área

El área ( A ) de un heptágono regular de lado a está dada por:

${\displaystyle A={\frac {7}{4}}a^{2}\cot {\frac {\pi }{7}}\simeq 3.634a^{2}.}$

Esto se puede ver subdividiendo el heptágono de un lado en siete "porciones de tarta" triangulares con vértices en el centro y en los vértices del heptágono, y luego dividiendo cada triángulo por la mitad utilizando la apotema como lado común. La apotema es la mitad de la cotangente de y el área de cada uno de los 14 triángulos pequeños es una cuarta parte de la apotema. ${\displaystyle \pi /7,}$

El área de un heptágono regular inscrito en un círculo de radio R es mientras que el área del círculo mismo es por lo tanto el heptágono regular llena aproximadamente 0,8710 de su círculo circunscrito. ${\displaystyle {\tfrac {7R^{2}}{2}}\sin {\tfrac {2\pi }{7}},}$ ${\displaystyle \pi R^{2};}$

Construcción

Como 7 es un primo de Pierpont pero no de Fermat , el heptágono regular no es construible con compás y regla , pero sí con regla marcada y compás. Es el polígono regular más pequeño con esta propiedad. Este tipo de construcción se llama construcción neusis . También es construible con compás, regla y trisectriz de ángulos. La imposibilidad de la construcción con regla y compás se deduce de la observación de que es un cero del cúbico irreducible x ³ + x ² − 2 x − 1 . En consecuencia, este polinomio es el polinomio mínimo de 2cos( 2π ⁄ 7 ), mientras que el grado del polinomio mínimo para un número construible debe ser una potencia de 2. ${\displaystyle \scriptstyle {2\cos {\tfrac {2\pi }{7}}\approx 1.247}}$

Heptágono con longitud lateral dada :
una animación de una construcción de neusis con regla marcada, según David Johnson Leisk ( Crockett Johnson ).

Aproximación

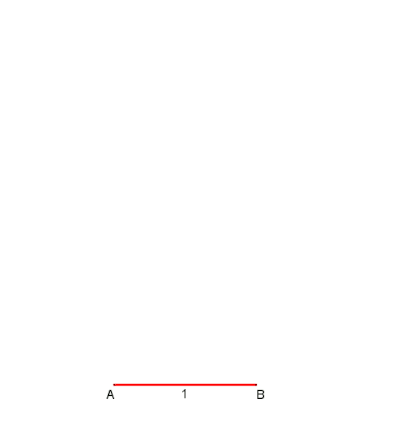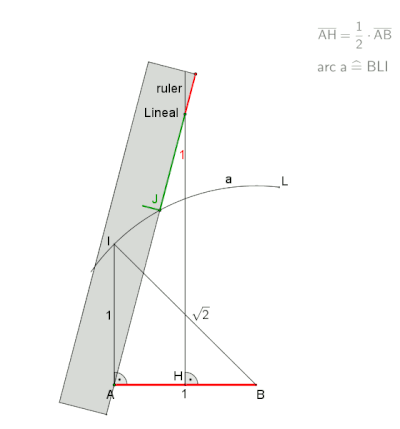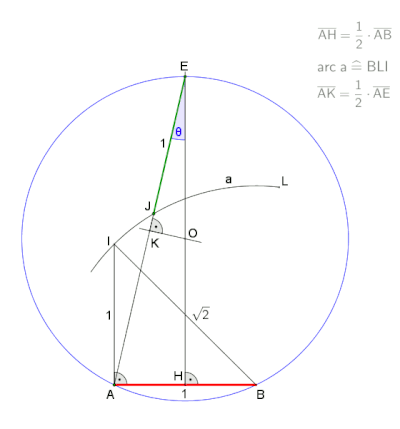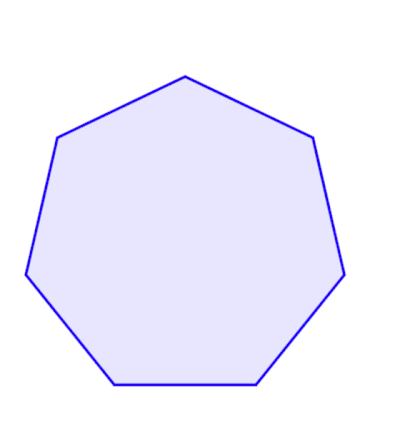
Una aproximación para uso práctico con un error de alrededor del 0,2% es utilizar la mitad del lado de un triángulo equilátero inscrito en el mismo círculo que la longitud del lado de un heptágono regular. Se desconoce quién encontró por primera vez esta aproximación, pero fue mencionada por Herón de Alejandría en la Métrica en el siglo I d. C., era bien conocida por los matemáticos islámicos medievales y se puede encontrar en la obra de Alberto Durero . ^{[2] [3]} Sea A sobre la circunferencia del círculo circunscrito. Dibuje el arco BOC . Luego da una aproximación para el borde del heptágono. ${\displaystyle \scriptstyle {BD={1 \over 2}BC}}$

Esta aproximación se utiliza para el lado del heptágono inscrito en el círculo unitario mientras que el valor exacto es . ${\displaystyle \scriptstyle {{\sqrt {3}} \over 2}\approx 0.86603}$ ${\displaystyle \scriptstyle 2\sin {\pi \over 7}\approx 0.86777}$

Ejemplo para ilustrar el error:
En un círculo circunscrito con radio r = 1 m , el error absoluto del primer lado sería aproximadamente -1,7 mm

Otras aproximaciones

Existen otras aproximaciones de un heptágono utilizando compás y regla, pero su dibujo requiere mucho tiempo. ^[4]

Simetría

Simetrías de un heptágono regular. Los vértices están coloreados según sus posiciones de simetría. Se dibujan líneas de espejo azules a través de los vértices y las aristas. Los órdenes de giro se dan en el centro. ^[5]

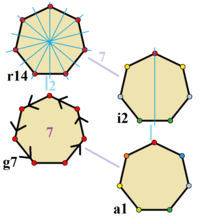
El heptágono regular pertenece al grupo puntual D 7h ( notación de Schoenflies ), orden 28. Los elementos de simetría son: un eje de rotación propio séptuple C ₇ , un eje de rotación impropio séptuple, S ₇ , 7 planos especulares verticales, σ _v , 7 ejes de rotación dobles, C ₂ , en el plano del heptágono y un plano especular horizontal, σ _h , también en el plano del heptágono. ^[6]

Diagonales y triángulo heptagonal

a = líneas rojas, b = azules, c = líneas verdes

El lado a del heptágono regular , la diagonal más corta b y la diagonal más larga c , con a < b < c , satisfacen ^{[7] : Lema 1}

${\displaystyle a^{2}=c(c-b),}$

${\displaystyle b^{2}=a(c+a),}$

${\displaystyle c^{2}=b(a+b),}$

${\displaystyle {\frac {1}{a}}={\frac {1}{b}}+{\frac {1}{c}}}$ (la ecuación óptica )

y por lo tanto

${\displaystyle ab+ac=bc,}$

y ^{[7] : Coro. 2}

${\displaystyle b^{3}+2b^{2}c-bc^{2}-c^{3}=0,}$

${\displaystyle c^{3}-2c^{2}a-ca^{2}+a^{3}=0,}$

${\displaystyle a^{3}-2a^{2}b-ab^{2}+b^{3}=0,}$

Por lo tanto, b / c , c / a y a / b satisfacen la ecuación cúbica. Sin embargo, no existen expresiones algebraicas con términos puramente reales para las soluciones de esta ecuación, porque es un ejemplo de casus irreducibilis . ${\displaystyle t^{3}-2t^{2}-t+1=0.}$

Las longitudes aproximadas de las diagonales en términos del lado del heptágono regular están dadas por

${\displaystyle b\approx 1.80193\cdot a,\qquad c\approx 2.24698\cdot a.}$

También tenemos ^[8]

${\displaystyle b^{2}-a^{2}=ac,}$

${\displaystyle c^{2}-b^{2}=ab,}$

${\displaystyle a^{2}-c^{2}=-bc,}$

y

${\displaystyle {\frac {b^{2}}{a^{2}}}+{\frac {c^{2}}{b^{2}}}+{\frac {a^{2}}{c^{2}}}=5.}$

Un triángulo heptagonal tiene vértices que coinciden con el primer, segundo y cuarto vértice de un heptágono regular (a partir de un vértice inicial arbitrario) y ángulos y, por lo tanto, sus lados coinciden con un lado y dos diagonales particulares del heptágono regular. ^[7] ${\displaystyle \pi /7,2\pi /7,}$ ${\displaystyle 4\pi /7.}$

En poliedros

Aparte del prisma heptagonal y del antiprisma heptagonal , ningún poliedro convexo formado enteramente por polígonos regulares contiene un heptágono como cara.

Heptágonos de estrella

Se pueden construir dos tipos de heptágonos estrellados ( heptagramas ) a partir de heptágonos regulares, etiquetados con los símbolos de Schläfli {7/2} y {7/3}, siendo el divisor el intervalo de conexión.

Heptágonos estrella azules, {7/2} y verdes {7/3} dentro de un heptágono rojo.

Alicatado y embalaje

Un triángulo regular, un heptágono y un cuadriágono pueden llenar completamente un vértice del plano . Sin embargo, no es posible realizar un mosaico del plano con solo estos polígonos, porque no hay forma de colocar uno de ellos en el tercer lado del triángulo sin dejar un espacio o crear una superposición. En el plano hiperbólico , es posible realizar mosaicos con heptágonos regulares. También es posible realizar mosaicos con heptágonos cóncavos en el plano euclidiano. ^[9]

El empaquetamiento reticular doble más denso del plano euclidiano por heptágonos regulares, que se conjetura que tiene la densidad de empaquetamiento máxima más baja de cualquier conjunto convexo

El heptágono regular tiene una densidad de empaquetamiento de red doble del plano euclidiano de aproximadamente 0,89269. Se ha conjeturado que esta es la densidad más baja posible para la densidad de empaquetamiento de red doble óptima de cualquier conjunto convexo y, de manera más general, para la densidad de empaquetamiento óptima de cualquier conjunto convexo. ^[10]

Ejemplos empíricos

El Reino Unido, desde 1982, tiene dos monedas heptagonales , las de 50p y 20p . El dólar de Barbados también es heptagonal. Estrictamente, la forma de las monedas es un heptágono Reuleaux , un heptágono curvilíneo que tiene curvas de ancho constante ; los lados están curvados hacia afuera para permitir que las monedas rueden suavemente cuando se insertan en una máquina expendedora . Las monedas de pula de Botsuana en las denominaciones de 2 pulas, 1 pula, 50 tebas y 5 tebas también tienen forma de heptágonos de curva equilátera. Las monedas con forma de heptágonos Reuleaux también están en circulación en Mauricio, Emiratos Árabes Unidos, Tanzania, Samoa, Papúa Nueva Guinea, Santo Tomé y Príncipe, Haití, Jamaica, Liberia, Ghana, Gambia, Jordania, Jersey, Guernsey, Isla de Man, Gibraltar, Guyana, Islas Salomón, Islas Malvinas y Santa Elena. La moneda de 1000 Kwacha de Zambia es un verdadero heptágono.

La moneda brasileña de 25 centavos tiene un heptágono inscrito en el disco de la moneda. Algunas versiones antiguas del escudo de armas de Georgia , incluso en la época soviética , usaban un heptagrama {7/2} como elemento.

Varias monedas, incluida la de 20 céntimos de euro , tienen simetría heptagonal en una forma llamada flor española .

En arquitectura, las plantas heptagonales son muy poco frecuentes. Un ejemplo notable es el Mausoleo del Príncipe Ernesto en Stadthagen , Alemania .

Muchas insignias de policía en los EE. UU. tienen un contorno de heptagrama {7/2}.

Véase también

• Heptagrama
• Polígono

Referencias

1. Gleason, Andrew Mattei (marzo de 1988). «Trisección de ángulos, heptágono y triscaidecágono pág. 186 (Fig.1) –187» (PDF) . The American Mathematical Monthly . 95 (3): 185–194. doi :10.2307/2323624. JSTOR  2323624. Archivado desde el original (PDF) el 19 de diciembre de 2015.
2. Hogendijk, Jan P. (1987). "Respuesta de Abu'l-Jūd a una pregunta de al-Bīrūnī sobre el heptágono regular" (PDF) . Anales de la Academia de Ciencias de Nueva York . 500 (1): 175–183. doi :10.1111/j.1749-6632.1987.tb37202.x.
3. GH Hughes, "Los polígonos de Alberto Durero-1525, El heptágono regular", Fig. 11 el lado del heptágono (7) Fig. 15, imagen del lado izquierdo, recuperada el 4 de diciembre de 2015
4. raumannkidwai. "Heptágono." Cuadro. Geogebra. Consultado el 20 de enero de 2024. https://www.geogebra.org/classic/CvsudDWr.
5. John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss , (2008) Las simetrías de las cosas, ISBN 978-1-56881-220-5 (Capítulo 20, Símbolos generalizados de Schaefli, Tipos de simetría de un polígono, págs. 275-278) 
6. Salthouse, JA; Ware, MJ (1972). Tablas de caracteres de grupos puntuales y datos relacionados. Cambridge: Cambridge University Press. ISBN 0-521-08139-4.
7. Abdilkadir Altintas, "Algunas colineales en el triángulo heptagonal", Forum Geometricorum 16, 2016, 249–256.http://forumgeom.fau.edu/FG2016volume16/FG201630.pdf
8. Leon Bankoff y Jack Garfunkel, "El triángulo heptagonal", Mathematics Magazine 46 (1), enero de 1973, 7–19.
9. Sycamore916, ed. "Heptágono". Wiki de Polytope. Última modificación: noviembre de 2023. Consultado el 20 de enero de 2024. https://polytope.miraheze.org/wiki/Heptagonal/Heptagon.
10. Kallus, Yoav (2015). "Formas de empaquetamiento pesimal". Geometría y topología . 19 (1): 343–363. arXiv : 1305.0289 . doi :10.2140/gt.2015.19.343. MR  3318753.

Enlaces externos

• Definición y propiedades de un heptágono Con animación interactiva
• Heptágono según Johnson
• Otro método de construcción aproximado
• Polígonos – Heptágonos
• Aproximación recientemente descubierta y muy precisa para la construcción de un heptágono regular.
• Heptágono, una construcción aproximada como animación
• Un heptágono con un lado dado, una construcción aproximada como animación

Heptágono