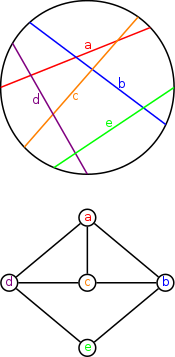
En teoría de grafos , un grafo circular es el grafo de intersección de un diagrama de cuerdas . Es decir, es un grafo no dirigido cuyos vértices pueden asociarse a un sistema finito de cuerdas de un círculo de modo que dos vértices sean adyacentes si y solo si las cuerdas correspondientes se cruzan entre sí.
Después de los algoritmos de tiempo polinomial anteriores , [1] Gioan et al. (2013) presentaron un algoritmo para reconocer gráficos circulares en tiempo casi lineal. Su método es más lento que el lineal por un factor de la función de Ackermann inversa y se basa en la búsqueda lexicográfica en amplitud . El tiempo de ejecución proviene de un método para mantener la descomposición dividida de un gráfico de forma incremental, a medida que se agregan vértices, utilizado como una subrutina en el algoritmo. [2]
Una serie de otros problemas que son NP-completos en grafos generales tienen algoritmos de tiempo polinomial cuando se restringen a grafos circulares. Por ejemplo, Kloks (1996) mostró que el ancho de árbol de un grafo circular se puede determinar, y construir una descomposición de árbol óptima, en tiempo O( n 3 ). Además, un relleno mínimo (es decir, un grafo cordal con la menor cantidad posible de aristas que contenga el grafo circular dado como un subgrafo) se puede encontrar en tiempo O( n 3 ). [3] Tiskin (2010) ha demostrado que una camarilla máxima de un grafo circular se puede encontrar en tiempo O( n log 2 n ), mientras que Nash y Gregg (2010) han demostrado que un conjunto independiente máximo de un grafo circular no ponderado se puede encontrar en tiempo O( n min{ d , α }), donde d es un parámetro del grafo conocido como su densidad, y α es el número de independencia del grafo circular.
Sin embargo, también hay problemas que siguen siendo NP-completos cuando se limitan a grafos circulares. Estos incluyen los problemas de conjunto dominante mínimo , conjunto dominante mínimo conexo y conjunto dominante total mínimo. [4]

El número cromático de un gráfico circular es el número mínimo de colores que se pueden utilizar para colorear sus cuerdas de modo que no haya dos cuerdas que se crucen con el mismo color. Dado que es posible formar gráficos circulares en los que conjuntos de cuerdas arbitrariamente grandes se crucen entre sí, el número cromático de un gráfico circular puede ser arbitrariamente grande, y determinar el número cromático de un gráfico circular es NP-completo. [5] Sigue siendo NP-completo comprobar si un gráfico circular puede colorearse con cuatro colores. [6] Unger (1992) afirmó que encontrar una coloración con tres colores se puede hacer en tiempo polinomial , pero su redacción de este resultado omite muchos detalles. [7]
Varios autores han investigado problemas de coloración de subclases restringidas de grafos circulares con pocos colores. En particular, para grafos circulares en los que ningún conjunto de k o más cuerdas se cruzan entre sí, es posible colorear el grafo con tan pocos colores como . Una forma de decir esto es que los grafos circulares están acotados . [8] En el caso particular cuando k = 3 (es decir, para grafos circulares sin triángulos ) el número cromático es como máximo cinco, y esto es estricto: todos los grafos circulares sin triángulos pueden colorearse con cinco colores, y existen grafos circulares sin triángulos que requieren cinco colores. [9] Si un grafo circular tiene una circunferencia de al menos cinco (es decir, no tiene triángulos y no tiene ciclos de cuatro vértices) puede colorearse con como máximo tres colores. [10] El problema de colorear grafos cuadrados sin triángulos es equivalente al problema de representar grafos cuadrados como subgrafos isométricos de productos cartesianos de árboles ; En esta correspondencia, el número de colores en la coloración corresponde al número de árboles en la representación del producto. [11]
Los gráficos circulares surgen en el diseño físico VLSI como una representación abstracta para un caso especial de enrutamiento de cables , conocido como "enrutamiento de caja de interruptores de dos terminales". En este caso, el área de enrutamiento es un rectángulo, todas las redes son de dos terminales y los terminales se colocan en el perímetro del rectángulo. Se ve fácilmente que el gráfico de intersección de estas redes es un gráfico circular. [12] Entre los objetivos del paso de enrutamiento de cables se encuentra garantizar que las diferentes redes permanezcan desconectadas eléctricamente y que sus posibles partes que se intersecan se deben disponer en diferentes capas conductoras. Por lo tanto, los gráficos circulares capturan varios aspectos de este problema de enrutamiento.
Las coloraciones de los grafos circulares también pueden utilizarse para encontrar incrustaciones de libros de grafos arbitrarios: si los vértices de un grafo G dado están dispuestos en un círculo, con los bordes de G formando cuerdas del círculo, entonces el grafo de intersección de estas cuerdas es un grafo circular y las coloraciones de este grafo circular son equivalentes a incrustaciones de libros que respetan el diseño circular dado. En esta equivalencia, la cantidad de colores en la coloración corresponde a la cantidad de páginas en la incrustación de libros. [6]

Un grafo es un grafo circular si y solo si es el grafo superpuesto de un conjunto de intervalos en una línea. Este es un grafo en el que los vértices corresponden a los intervalos, y dos vértices están conectados por una arista si los dos intervalos se superponen, sin que ninguno contenga al otro.
El gráfico de intersección de un conjunto de intervalos en una línea se llama gráfico de intervalo .
Los gráficos de cadenas , los gráficos de intersección de curvas en el plano, incluyen gráficos circulares como un caso especial.
Todo grafo hereditario de distancia es un grafo circular, al igual que todo grafo de permutación y todo grafo de indiferencia . Todo grafo plano exterior es también un grafo circular. [13]
Los grafos circulares se generalizan mediante los grafos polígono-círculo , grafos de intersección de polígonos todos inscritos en el mismo círculo. [14]