En teoría de grafos , un grafo bivariado es un grafo cuyo conjunto de vértices se puede dividir en dos partes iguales de modo que cada vértice es adyacente a exactamente un vértice del otro conjunto que no lo contiene. [1] [2] [3] En un grafo bivariado G con 2 n vértices, existe un conjunto de n aristas independientes de modo que ningún número impar de ellas se encuentra en un ciclo de G.
El grafo de Petersen , que se muestra a continuación, es un grafo bivariado: si se divide en un pentágono exterior y una estrella interior de cinco puntas, cada vértice de un lado de la partición tiene exactamente un vecino en el otro lado de la partición. En términos más generales, lo mismo es cierto para cualquier grafo de Petersen generalizado formado al conectar un polígono exterior y una estrella interior con el mismo número de puntas; por ejemplo, esto se aplica al grafo de Möbius-Kantor y al grafo de Desargues .

Cualquier gráfico de hipercubo , como el hipercubo de cuatro dimensiones que se muestra a continuación, también es bivariado.

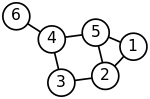
Sin embargo, el gráfico que se muestra a continuación no es bivariado. Cualquiera que sea la opción que elijamos para las tres aristas independientes, una de ellas es una arista de un ciclo.
Un árbol T con 2 n vértices, es bivariado si y sólo si el número de independencia de T es n , o, equivalentemente, si y sólo si tiene un emparejamiento perfecto . [1]
El grafo k -varigado , k ≥ 3, se puede definir de manera similar. Se dice que un grafo es k -varigado si su conjunto de vértices se puede dividir en k partes iguales de modo que cada vértice sea adyacente a exactamente un vértice de cada otra parte que no lo contenga. [2]