Pérdida de Huber

Función de pérdida utilizada en regresión robusta

En estadística , la pérdida de Huber es una función de pérdida utilizada en regresión robusta , que es menos sensible a valores atípicos en los datos que la pérdida de error al cuadrado . A veces también se utiliza una variante para la clasificación.

Definición

Pérdida de Huber (verde ) y pérdida por error al cuadrado (azul) en función de ${\displaystyle \delta =1}$ ${\displaystyle y-f(x)}$

La función de pérdida de Huber describe la penalización incurrida por un procedimiento de estimación f . Huber (1964) define la función de pérdida por partes mediante ^[1]

${\displaystyle L_{\delta }(a)={\begin{cases}{\frac {1}{2}}{a^{2}}&{\text{for }}|a|\leq \delta ,\\\delta \cdot \left(|a|-{\frac {1}{2}}\delta \right),&{\text{otherwise.}}\end{cases}}}$

Esta función es cuadrática para valores pequeños de a y lineal para valores grandes, con valores y pendientes iguales de las diferentes secciones en los dos puntos donde . La variable a a menudo se refiere a los residuos, es decir, a la diferencia entre los valores observados y predichos , por lo que el primero se puede ampliar a ^[2] ${\displaystyle |a|=\delta }$ ${\displaystyle a=y-f(x)}$

${\displaystyle L_{\delta }(y,f(x))={\begin{cases}{\frac {1}{2}}(y-f(x))^{2}&{\text{for }}|y-f(x)|\leq \delta ,\\\delta \ \cdot \left(|y-f(x)|-{\frac {1}{2}}\delta \right),&{\text{otherwise.}}\end{cases}}}$

La pérdida de Huber es la convolución de la función de valor absoluto con la función rectangular , escalada y traducida. De este modo "suaviza" la esquina del primero en el origen.

Comparación de la pérdida de Huber con otras funciones de pérdida utilizadas para una regresión robusta.

Motivación

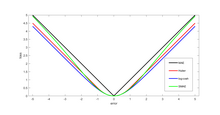
Dos funciones de pérdida muy utilizadas son la pérdida al cuadrado , y la pérdida absoluta . La función de pérdida al cuadrado da como resultado un estimador insesgado de media aritmética , y la función de pérdida de valor absoluto da como resultado un estimador insesgado de mediana (en el caso unidimensional, y un estimador insesgado de mediana geométrica para el caso multidimensional). La pérdida al cuadrado tiene la desventaja de que tiende a estar dominada por valores atípicos: cuando se suma un conjunto de (como en ), la media muestral está demasiado influenciada por unos pocos valores particularmente grandes cuando la distribución tiene colas pesadas. : en términos de teoría de la estimación , la eficiencia relativa asintótica de la media es pobre para distribuciones de colas pesadas. ${\displaystyle L(a)=a^{2}}$ ${\displaystyle L(a)=|a|}$ ${\displaystyle a}$ ${\textstyle \sum _{i=1}^{n}L(a_{i})}$ ${\displaystyle a}$

Como se definió anteriormente, la función de pérdida de Huber es fuertemente convexa en una vecindad uniforme de su mínimo ; en el límite de esta vecindad uniforme, la función de pérdida de Huber tiene una extensión diferenciable a una función afín en los puntos y . Estas propiedades le permiten combinar gran parte de la sensibilidad del estimador de varianza mínima insesgada de la media (usando la función de pérdida cuadrática) y la robustez del estimador insesgado de la mediana (usando la función de valor absoluto). ${\displaystyle a=0}$ ${\displaystyle a=-\delta }$ ${\displaystyle a=\delta }$

Función de pérdida pseudo-Huber

La función de pérdida Pseudo-Huber se puede utilizar como una aproximación suave de la función de pérdida de Huber. Combina las mejores propiedades de la pérdida al cuadrado L2 y la pérdida absoluta L1 al ser fuertemente convexo cuando está cerca del objetivo/mínimo y menos pronunciado para valores extremos. La escala en la que la función de pérdida Pseudo-Huber pasa de la pérdida L2 para valores cercanos al mínimo a la pérdida L1 para valores extremos y la pendiente en valores extremos se puede controlar mediante el valor. La función de pérdida Pseudo-Huber garantiza que las derivadas sean continuas para todos los grados. Se define como ^{[3] [4]} ${\displaystyle \delta }$

${\displaystyle L_{\delta }(a)=\delta ^{2}\left({\sqrt {1+(a/\delta )^{2}}}-1\right).}$

Como tal, esta función se aproxima para valores pequeños de y se aproxima a una línea recta con pendiente para valores grandes de . ${\displaystyle a^{2}/2}$ ${\displaystyle a}$ ${\displaystyle \delta }$ ${\displaystyle a}$

Si bien la anterior es la forma más común, también existen otras aproximaciones suaves de la función de pérdida de Huber. ^[5]

Variante de clasificación

Para fines de clasificación , a veces se utiliza una variante de la pérdida de Huber llamada Huber modificada . Dada una predicción (una puntuación de clasificador de valor real) y una etiqueta de clase binaria verdadera , la pérdida de Huber modificada se define como ^[6] ${\displaystyle f(x)}$ ${\displaystyle y\in \{+1,-1\}}$

${\displaystyle L(y,f(x))={\begin{cases}\max(0,1-y\,f(x))^{2}&{\textrm {for}}\,\,y\,f(x)>-1,\\-4y\,f(x)&{\textrm {otherwise.}}\end{cases}}}$

El término es la pérdida de bisagra utilizada por las máquinas de vectores de soporte ; la pérdida de bisagra suavizada cuadráticamente es una generalización de . ^[6] ${\displaystyle \max(0,1-y\,f(x))}$ ${\displaystyle L}$

Aplicaciones

La función de pérdida de Huber se utiliza en estadística robusta , estimación M y modelado aditivo . ^[7]

Ver también

• Winsorizar
• Regresión robusta
• estimador m
• Comparación visual de diferentes estimadores M.

Referencias

1. Huber, Peter J. (1964). "Estimación robusta de un parámetro de ubicación". Anales de Estadística . 53 (1): 73–101. doi : 10.1214/aoms/1177703732 . JSTOR  2238020.
2. Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). Los elementos del aprendizaje estadístico. pag. 349. Archivado desde el original el 26 de enero de 2015.En comparación con Hastie et al. , la pérdida se escala por un factor de ⁠1/2⁠ , para ser coherente con la definición original de Huber dada anteriormente.
3. Charbonnier, P.; Blanc-Féraud, L .; Aubert, G.; Barlaud, M. (1997). "Regularización determinista que preserva los bordes en imágenes computarizadas". Traducción IEEE. Proceso de imagen . 6 (2): 298–311. Código Bib : 1997ITIP....6..298C. CiteSeerX 10.1.1.64.7521 . doi : 10.1109/83.551699. PMID  18282924. 
4. Hartley, R.; Zisserman, A. (2003). Geometría de vista múltiple en visión por computadora (2ª ed.). Prensa de la Universidad de Cambridge. pag. 619.ISBN​ 978-0-521-54051-3.
5. Lange, K. (1990). "Convergencia de algoritmos de reconstrucción de imágenes con suavizado de Gibbs". Traducción IEEE. Medicina. Imágenes . 9 (4): 439–446. doi : 10.1109/42.61759. PMID  18222791.
6. Zhang, Tong (2004). Resolver problemas de predicción lineal a gran escala utilizando algoritmos de descenso de gradiente estocásticos. ICML.
7. Friedman, JH (2001). "Aproximación de funciones codiciosas: una máquina de aumento de gradiente". Anales de Estadística . 26 (5): 1189-1232. doi : 10.1214/aos/1013203451 . JSTOR  2699986.