Fuerza entre imanes

Fuerza debida al campo magnético

Los imanes ejercen fuerzas y pares entre sí a través de la interacción de sus campos magnéticos . Las fuerzas de atracción y repulsión son el resultado de estas interacciones. El campo magnético de cada imán se debe a corrientes microscópicas de electrones cargados eléctricamente que orbitan alrededor de los núcleos y al magnetismo intrínseco de las partículas fundamentales (como los electrones) que componen el material. Ambos se modelan bastante bien como pequeños bucles de corriente llamados dipolos magnéticos que producen su propio campo magnético y se ven afectados por campos magnéticos externos. La fuerza más elemental entre imanes es la interacción dipolo-dipolo magnético . Si se conocen todos los dipolos magnéticos de cada imán, entonces la fuerza neta sobre ambos imanes se puede determinar sumando todas las interacciones entre los dipolos del primer imán y los dipolos del segundo imán.

A menudo resulta más conveniente modelar la fuerza entre dos imanes como si se debiera a las fuerzas entre polos magnéticos que tienen cargas magnéticas repartidas entre ellos. La carga magnética positiva y negativa siempre está conectada por una cuerda de material magnetizado; no existe carga magnética aislada. Este modelo funciona bien para predecir las fuerzas entre imanes simples cuando se dispone de buenos modelos de cómo se distribuye la carga magnética.

Polos magnéticos vs corrientes atómicas

El modelo de polo magnético para H y el modelo de bucle amperiano para B dan como resultado un campo idéntico en el exterior del imán, pero en el interior son muy diferentes.

El campo de un imán es la suma de los campos de todos los elementos de volumen magnetizados , que consisten en pequeños dipolos magnéticos a nivel atómico. La suma directa de todos esos campos dipolares requiere una integración tridimensional para obtener el campo de un imán, lo que puede ser complicado.

En el caso de la magnetización homogénea, el problema se puede simplificar de dos maneras diferentes, utilizando el teorema de Stokes . Al integrar a lo largo de la dirección de magnetización, todos los dipolos a lo largo de la línea de integración se cancelan entre sí, excepto en la superficie final del imán. El campo surge entonces solo de aquellas cargas magnéticas (matemáticas) distribuidas sobre las facetas finales del imán. Por el contrario, al integrar sobre un área magnetizada ortogonal a la dirección de magnetización, los dipolos dentro de esta área se cancelan entre sí , excepto en la superficie exterior del imán, donde (matemáticamente) se suman para formar una corriente de anillo. Esto se llama modelo de bucle de Ampère. En ambos modelos, solo se deben considerar distribuciones bidimensionales sobre la superficie del imán, lo que es más simple que el problema tridimensional original.

Modelo de polo magnético : En el modelo de polo magnético, se imagina que las superficies polares de un imán permanente están cubiertas con la llamada carga magnética , partículas del polo norte en el polo norte y partículas del polo sur en el polo sur, que son la fuente de las líneas de campo magnético. El campo debido a las cargas magnéticas se obtiene a través de la ley de Coulomb con cargas magnéticas en lugar de cargas eléctricas. Si se conoce la distribución de polos magnéticos, entonces el modelo de polo magnético proporciona la distribución exacta de la intensidad del campo magnético H tanto dentro como fuera del imán. La distribución de carga superficial es uniforme, si el imán está magnetizado de forma homogénea y tiene facetas finales planas (como un cilindro o un prisma).

Modelo de bucle de Ampère : En el modelo de bucle de Ampère , toda la magnetización se debe al efecto de corrientes circulares atómicas o microscópicas , también llamadas corrientes de Ampère , en todo el material. El efecto neto de estas corrientes microscópicas es hacer que el imán se comporte como si hubiera una corriente eléctrica macroscópica fluyendo en bucles en el imán con el campo magnético normal a los bucles. El campo debido a tales corrientes se obtiene a través de la ley de Biot-Savart . El modelo de bucle de Ampère proporciona la densidad de flujo magnético correcta B tanto dentro como fuera del imán. A veces es difícil calcular las corrientes de Ampère en la superficie de un imán.

Momento dipolar magnético

Lejos de un imán, su campo magnético casi siempre se describe (con una buena aproximación) mediante un campo dipolar caracterizado por su momento dipolar magnético total , m . Esto es así independientemente de la forma del imán, siempre que el momento magnético no sea cero. Una característica de un campo dipolar es que la intensidad del campo disminuye inversamente con el cubo de la distancia desde el centro del imán.

El momento magnético de un imán es, por tanto, una medida de su fuerza y ​​orientación. Un bucle de corriente eléctrica , una barra magnética , un electrón , una molécula y un planeta tienen momentos magnéticos. Más precisamente, el término momento magnético normalmente se refiere al momento dipolar magnético de un sistema , que produce el primer término en la expansión multipolar ^{[nota 1]} de un campo magnético general.

Tanto el par como la fuerza ejercida sobre un imán por un campo magnético externo son proporcionales al momento magnético de ese imán. El momento magnético es un vector : tiene una magnitud y una dirección. La dirección del momento magnético apunta del polo sur al polo norte de un imán (dentro del imán). Por ejemplo, la dirección del momento magnético de un imán de barra, como el de una brújula, es la dirección hacia la que apuntan los polos norte.

En el modelo de bucle amperiano físicamente correcto, los momentos dipolares magnéticos se deben a bucles infinitesimalmente pequeños de corriente. Para un bucle de corriente suficientemente pequeño, I , y área, A , el momento dipolar magnético es: donde la dirección de m es normal al área en una dirección determinada utilizando la corriente y la regla de la mano derecha . Como tal, la unidad SI del momento dipolar magnético es amperio  metro ² . Más precisamente, para tener en cuenta los solenoides con muchas vueltas, la unidad del momento dipolar magnético es amperio-vuelta metro ² . $${\displaystyle \mathbf {m} =I\mathbf {A} ,}$$

En el modelo de polo magnético, el momento dipolar magnético se debe a dos cargas magnéticas iguales y opuestas que están separadas por una distancia, d . En este modelo, m es similar al momento dipolar eléctrico p debido a las cargas eléctricas: donde q _m es la "carga magnética". La dirección del momento dipolar magnético apunta desde el polo sur negativo al polo norte positivo de este pequeño imán. $${\displaystyle m=q_{\mathrm {m} }d,}$$

Fuerza magnética debido a un campo magnético no uniforme

Arriba: la fuerza sobre los polos norte magnéticos. Abajo: la fuerza sobre dipolos alineados, como las partículas de hierro. ${\displaystyle \mathbf {B} }$
${\displaystyle \mathbf {\nabla } |\mathbf {B} |}$

Los imanes se atraen a lo largo del gradiente del campo magnético. El ejemplo más simple de esto es la atracción de los polos opuestos de dos imanes. Cada imán produce un campo magnético que es más fuerte cerca de sus polos. Si los polos opuestos de dos imanes separados están uno frente al otro, cada uno de los imanes es atraído hacia el campo magnético más fuerte cerca del polo del otro. Sin embargo, si los polos iguales están uno frente al otro, son repelidos por el campo magnético más grande.

El modelo de polos magnéticos predice una forma matemática correcta para esta fuerza y ​​es más fácil de entender cualitativamente. Si se coloca un imán en un campo magnético uniforme, ambos polos sentirán la misma fuerza magnética pero en direcciones opuestas, ya que tienen carga magnética opuesta. Pero, cuando se coloca un imán en un campo no uniforme, como el debido a otro imán, el polo que experimenta el campo magnético grande experimentará la fuerza grande y habrá una fuerza neta sobre el imán. Si el imán está alineado con el campo magnético, lo que corresponde a dos imanes orientados en la misma dirección cerca de los polos, entonces será atraído hacia el campo magnético más grande. Si está alineado de manera opuesta, como el caso de dos imanes con polos iguales enfrentados entre sí, entonces el imán será repelido de la región de campo magnético más alto.

En el modelo de bucle de Ampèrian, también hay una fuerza sobre un dipolo magnético debido a un campo magnético no uniforme, pero esto se debe a fuerzas de Lorentz sobre el bucle de corriente que forma el dipolo magnético. La fuerza obtenida en el caso de un modelo de bucle de corriente es donde el gradiente ∇ es el cambio de la cantidad m · B por unidad de distancia, y la dirección es la del aumento máximo de m · B . Para entender esta ecuación, observe que el producto escalar m · B = mB cos( θ ) , donde m y B representan la magnitud de los vectores m y B y θ es el ángulo entre ellos. Si m está en la misma dirección que B , entonces el producto escalar es positivo y el gradiente apunta 'cuesta arriba' tirando del imán hacia regiones de mayor campo B (más estrictamente m  ·  B más grande ). B representa la fuerza y ​​la dirección del campo magnético. Esta ecuación es estrictamente válida solo para imanes de tamaño cero, pero a menudo es una buena aproximación para imanes no demasiado grandes. La fuerza magnética sobre imanes más grandes se determina dividiéndolos en regiones más pequeñas que tienen su propio m y luego sumando las fuerzas en cada una de estas regiones. $${\displaystyle \mathbf {F} =\nabla \left(\mathbf {m} \cdot \mathbf {B} \right),}$$

Modelo de polo magnético

El modelo de polos magnéticos supone que las fuerzas magnéticas entre imanes se deben a cargas magnéticas cerca de los polos. Este modelo funciona incluso cerca del imán cuando el campo magnético se vuelve más complicado y depende más de la forma detallada y la magnetización del imán que solo de la contribución del dipolo magnético. Formalmente, el campo se puede expresar como una expansión multipolar : un campo dipolar, más un campo cuadrupolar , más un campo octopolar, etc. en el modelo de bucle de Ampère, pero esto puede ser muy engorroso matemáticamente.

Calcular la fuerza magnética

Calcular la fuerza de atracción o repulsión entre dos imanes es, en general, una operación muy compleja, ya que depende de la forma, magnetización, orientación y separación de los imanes. El modelo de polos magnéticos depende de cierto conocimiento de cómo se distribuye la "carga magnética" entre los polos magnéticos. Incluso en ese caso, sólo es verdaderamente útil para configuraciones simples. Afortunadamente, esta restricción cubre muchos casos útiles.

Fuerza entre dos polos magnéticos

Si ambos polos son lo suficientemente pequeños como para ser representados como puntos individuales, entonces pueden considerarse cargas magnéticas puntuales. Clásicamente , la fuerza entre dos polos magnéticos viene dada por: ^[1]

$${\displaystyle F={{\mu q_{m1}q_{m2}} \over {4\pi r^{2}}}}$$dónde

• F es fuerza (unidad SI: newton )
• q _{m 1} y q _{m 2} son las magnitudes de la carga magnética en los polos magnéticos (unidad SI: amperio - metro )
• μ es la permeabilidad del medio intermedio (unidad SI: tesla metro por amperio , henrio por metro o newton por amperio al cuadrado)
• r es la separación (unidad SI: metro).

La descripción de los polos es útil para los magnetistas que diseñan imanes del mundo real, pero los imanes reales tienen una distribución de polos más compleja que un único norte y sur. Por lo tanto, la implementación de la idea de los polos no es sencilla. En algunos casos, una de las fórmulas más complejas que se dan a continuación será más útil.

Fuerza entre dos superficies magnetizadas cercanas de áreaA

La fuerza mecánica entre dos superficies magnetizadas cercanas se puede calcular con la siguiente ecuación. La ecuación es válida solo para los casos en los que el efecto de la formación de franjas es despreciable y el volumen del entrehierro es mucho menor que el del material magnetizado, la fuerza para cada superficie magnetizada es: ^{[2] [3] [4]} donde: $${\displaystyle F={\frac {\mu _{0}H^{2}A}{2}}={\frac {B^{2}A}{2\mu _{0}}}}$$

• A es el área de cada superficie, en ^m2
• H es su campo magnetizante , en A/m.
• μ ₀ es la permeabilidad del espacio , que es igual a 4π×10 ⁻⁷  T·m/A
• B es la densidad de flujo , en T

La derivación de esta ecuación es análoga a la fuerza entre dos superficies cercanas cargadas eléctricamente, ^[5] que supone que el campo entre las placas es uniforme.

Fuerza entre dos imanes de barra

Campo de dos imanes de barra cilíndricos que se atraen

Campo de dos imanes de barra cilíndricos que se repelen

La fuerza entre dos imanes de barra cilíndricos idénticos colocados uno junto a otro a gran distancia es aproximadamente: ^[2] donde ${\displaystyle x\gg R}$ $${\displaystyle F\simeq \left[{\frac {B_{0}^{2}A^{2}\left(L^{2}+R^{2}\right)}{\pi \mu _{0}L^{2}}}\right]\left[{\frac {1}{x^{2}}}+{\frac {1}{(x+2L)^{2}}}-{\frac {2}{(x+L)^{2}}}\right]}$$

• B ₀ es la densidad de flujo muy cercana a cada polo, en T,
• A es el área de cada polo, en m ² ,
• L es la longitud de cada imán, en m,
• R es el radio de cada imán, en m, y
• x es la separación entre los dos imanes, en m

$${\displaystyle B_{0}={\frac {\mu _{0}}{2}}M}$$relaciona la densidad de flujo en el polo con la magnetización del imán.

Tenga en cuenta que estas formulaciones suponen distribuciones puntuales de carga magnética en lugar de una distribución uniforme sobre las facetas de los extremos, lo que constituye una buena aproximación solo a distancias relativamente grandes. Para distancias intermedias, se deben utilizar métodos numéricos .

Fuerza entre dos imanes cilíndricos

Fuerza exacta entre dos barras magnéticas cilíndricas coaxiales para varias relaciones de aspecto.

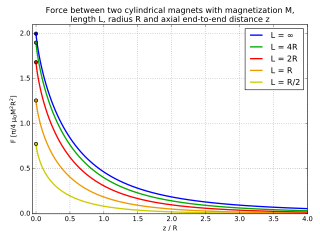
Para dos imanes cilíndricos con radios iguales , longitudes y , y dado un gran espacio lateral entre ellos, en el límite , la fuerza se puede aproximar mediante ^[6] ${\displaystyle R}$ ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle x\gg R}$

${\displaystyle F(x,r)\simeq {\frac {\pi K_{d}}{2}}R^{4}\sum _{i,j=0}^{1}{\left({\frac {(-1)^{i+j}}{(x+iL_{1}+jL_{2})^{2}}}\left(1-{\frac {3}{2}}{\frac {r^{2}}{(x+iL_{1}+jL_{2})^{2}}}\right)\right)}}$

dónde

• ${\displaystyle R}$es el radio de cada uno de los dos imanes, bajo el supuesto de radios iguales
• ${\displaystyle L_{1}}$es la longitud del primer imán
• ${\displaystyle L_{2}}$es la longitud del segundo imán
• ${\displaystyle K_{d}}$es el producto energético máximo en unidades de J/m ³ (julios por metro cúbico)
• ${\displaystyle x}$es la distancia normal entre las dos caras paralelas de los imanes
• ${\displaystyle r}$es la distancia entre los ejes dipolares magnéticos de los dos imanes.

Con su dipolo magnético alineado, la fuerza se puede calcular analíticamente utilizando integrales elípticas . ^[7]

$${\displaystyle F(x)\simeq {\frac {\pi K_{d}}{2}}R^{4}\left[{\frac {1}{x^{2}}}+{\frac {1}{(x+2L)^{2}}}-{\frac {2}{(x+L)^{2}}}\right]}$$

Esto se puede reescribir como,

$${\displaystyle F(x)\simeq {\frac {\pi \mu _{0}}{4}}M^{2}R^{4}\left[{\frac {1}{x^{2}}}+{\frac {1}{(x+2L)^{2}}}-{\frac {2}{(x+L)^{2}}}\right]}$$

¿Dónde está la magnetización de los imanes y es la distancia entre ellos? Para valores pequeños de , los resultados son erróneos ya que la fuerza se vuelve grande para distancias cercanas a cero. ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle x}$

Si el imán es largo ( ), una medición de la densidad de flujo magnético muy cercana al imán está relacionada aproximadamente con la fórmula ${\displaystyle L\gg R}$ ${\displaystyle B_{0}}$ ${\displaystyle M}$ $${\displaystyle B_{0}={\frac {\mu _{0}}{2}}M.}$$

El momento dipolar magnético efectivo se puede escribir como donde es el volumen del imán. Para un cilindro, es , y es el campo de magnetización del dipolo. $${\displaystyle m=MV}$$ ${\displaystyle V}$ ${\displaystyle V=\pi R^{2}L}$ ${\displaystyle M}$

Cuando se obtiene la aproximación del dipolo puntual, ${\displaystyle L\ll x}$ $${\displaystyle F(x)={\frac {3\pi \mu _{0}}{2}}M^{2}R^{4}L^{2}{\frac {1}{x^{4}}}={\frac {3\mu _{0}}{2\pi }}M^{2}V^{2}{\frac {1}{x^{4}}}={\frac {3\mu _{0}}{2\pi }}m_{1}m_{2}{\frac {1}{x^{4}}}}$$

Que coincide con la expresión de la fuerza entre dos dipolos magnéticos.

Modelo de bucle amperiano

El científico francés André Marie Ampère descubrió que el magnetismo producido por imanes permanentes y el magnetismo producido por electroimanes son del mismo tipo. Por ello, la fuerza de un imán permanente puede expresarse en los mismos términos que la de un electroimán.

La fuerza del magnetismo de un electroimán, que es un bucle plano de alambre por el que fluye una corriente, medida a una distancia grande en comparación con el tamaño del bucle, es proporcional a esa corriente y es proporcional al área de superficie de ese bucle.

Para expresar la fuerza de un imán permanente en los mismos términos que la de un electroimán, se piensa que un imán permanente contiene pequeños bucles de corriente en todo su volumen, y luego se descubre que la fuerza magnética de ese imán es proporcional a la corriente de cada bucle (en amperios), y proporcional a la superficie de cada bucle (en metros cuadrados), y proporcional a la densidad de bucles de corriente en el material (en unidades por metro cúbico), por lo que la dimensión de la fuerza del magnetismo de un imán permanente es amperios por metros cuadrados por metro cúbico, es amperios por metro.

Es por eso que el amperio por metro es la unidad correcta de magnetismo, aunque estos pequeños bucles de corriente no estén realmente presentes en un imán permanente.

La validez del modelo de Ampère significa que es admisible pensar en el material magnético como si estuviera formado por bucles de corriente, y el efecto total es la suma del efecto de cada bucle de corriente, y así el efecto magnético de un imán real puede calcularse como la suma de los efectos magnéticos de pequeños trozos de material magnético que están a una distancia que es grande en comparación con el tamaño de cada trozo.

Esto es muy útil para calcular el campo de fuerza magnética de un imán real; implica sumar una gran cantidad de fuerzas pequeñas y no debe hacerlo a mano, sino dejar que su computadora lo haga por usted; todo lo que el programa de computadora necesita saber es la fuerza entre pequeños imanes que están a gran distancia entre sí.

En estos cálculos se suele suponer que cada pequeño trozo de material magnético (del mismo tamaño) tiene un magnetismo igualmente fuerte, pero esto no siempre es cierto: un imán que se coloca cerca de otro imán puede cambiar la magnetización de ese otro imán. En el caso de los imanes permanentes, esto suele ser solo un cambio pequeño, pero si tienes un electroimán que consiste en un cable enrollado alrededor de un núcleo de hierro y acercas un imán permanente a ese núcleo, entonces la magnetización de ese núcleo puede cambiar drásticamente (por ejemplo, si no hay corriente en el cable, el electroimán no sería magnético, pero cuando se acerca el imán permanente, el núcleo del electroimán se vuelve magnético).

Por tanto, el modelo de Ampère es adecuado para calcular el campo de fuerza magnética de un imán permanente, pero para los electroimanes puede ser mejor utilizar un enfoque de circuito magnético.

Interacción magnética dipolo-dipolo

Si dos o más imanes son lo suficientemente pequeños o están lo suficientemente distantes como para que su forma y tamaño no sean importantes, entonces ambos imanes pueden modelarse como dipolos magnéticos que tienen momentos magnéticos m ₁ y m ₂ . En el caso de imanes esféricos magnetizados uniformemente, este modelo es preciso incluso a un tamaño y una distancia finitos, ya que el campo exterior de dichos imanes es exactamente un campo dipolar. ^[8]

Campo magnético de un dipolo ideal.

El campo magnético de un dipolo magnético en notación vectorial es: donde $${\displaystyle \mathbf {B} (\mathbf {m} ,\mathbf {r} )={\frac {\mu _{0}}{4\pi r^{3}}}\left(3(\mathbf {m} \cdot {\hat {\mathbf {r} }}){\hat {\mathbf {r} }}-\mathbf {m} \right)+{\frac {2\mu _{0}}{3}}\mathbf {m} \delta ^{3}(\mathbf {r} )}$$

• B es el campo
• r es el vector desde la posición del dipolo hasta la posición donde se mide el campo
• r es el valor absoluto de r : la distancia desde el dipolo
• ${\displaystyle {\hat {\mathbf {r} }}=\mathbf {r} /r}$es el vector unitario paralelo a r ;
• m es el momento dipolar (vectorial)
• μ ₀ es la permeabilidad del espacio libre
• δ ^{3 es la} función delta tridimensional . ^{[nota 2]}

Este es exactamente el campo de un dipolo puntual, exactamente el término dipolar en la expansión multipolar de un campo arbitrario, y aproximadamente el campo de cualquier configuración tipo dipolo a grandes distancias.

Marcos de referencia para el cálculo de las fuerzas entre dos dipolos

Fuerza entre imanes cilíndricos coaxiales. Según la aproximación dipolar, la fuerza disminuye proporcionalmente a para distancias grandes z , lo que da como resultado pendientes de −4 en el gráfico logarítmico-logarítmico . ${\displaystyle 1/z^{4}}$

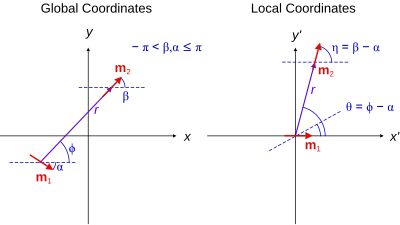
Si el sistema de coordenadas se desplaza para centrarlo en m ₁ y se rota de manera que el eje x apunte en la dirección de m ₁ , la ecuación anterior se simplifica a ^[9], donde las variables r y θ se miden en un marco de referencia con origen en m ₁ y orientado de manera que m ₁ esté en el origen apuntando en la dirección x. Este marco se denomina coordenadas locales y se muestra en la figura de la derecha. $${\displaystyle {\begin{aligned}B_{x}(\mathbf {r} )&={\frac {\mu _{0}}{4\pi }}m_{1}\left({\frac {3\cos ^{2}\theta -1}{r^{3}}}\right)\\B_{y}(\mathbf {r} )&={\frac {\mu _{0}}{4\pi }}m_{1}\left({\frac {3\cos \theta \sin \theta }{r^{3}}}\right),\end{aligned}}}$$

La fuerza de un dipolo magnético sobre otro se determina utilizando el campo magnético del primer dipolo dado anteriormente y determinando la fuerza debida al campo magnético sobre el segundo dipolo utilizando la ecuación de fuerza dada anteriormente. Utilizando la notación vectorial, la fuerza de un dipolo magnético m ₁ sobre el dipolo magnético m ₂ es: donde r es el vector de distancia desde el momento dipolar m ₁ hasta el momento dipolar m ₂ , con r = ‖ r ‖ . La fuerza que actúa sobre m ₁ es en dirección opuesta. Como ejemplo, la fuerza magnética para dos imanes que apuntan en la dirección z y están alineados en el eje z y separados por la distancia z es: $${\displaystyle \mathbf {F} (\mathbf {r} ,\mathbf {m} _{1},\mathbf {m} _{2})={\frac {3\mu _{0}}{4\pi r^{5}}}\left[(\mathbf {m} _{1}\cdot \mathbf {r} )\mathbf {m} _{2}+(\mathbf {m} _{2}\cdot \mathbf {r} )\mathbf {m} _{1}+(\mathbf {m} _{1}\cdot \mathbf {m} _{2})\mathbf {r} -{\frac {5(\mathbf {m} _{1}\cdot \mathbf {r} )(\mathbf {m} _{2}\cdot \mathbf {r} )}{r^{2}}}\mathbf {r} \right]}$$

${\displaystyle \mathbf {F} (z,m_{1},m_{2})=-{\frac {3\mu _{0}m_{1}m_{2}}{2\pi z^{4}}}}$, dirección z.

A continuación se muestran las fórmulas finales, expresadas en el sistema de coordenadas global. $${\displaystyle {\begin{aligned}F_{r}(\mathbf {r} ,\alpha ,\beta )&=-{\frac {3\mu _{0}}{4\pi }}{\frac {m_{2}m_{1}}{r^{4}}}\left[2\cos(\phi -\alpha )\cos(\phi -\beta )-\sin(\phi -\alpha )\sin(\phi -\beta )\right]\\F_{\phi }(\mathbf {r} ,\alpha ,\beta )&=-{\frac {3\mu _{0}}{4\pi }}{\frac {m_{2}m_{1}}{r^{4}}}\sin(2\phi -\alpha -\beta )\end{aligned}}}$$

Notas

1. La parte dipolar magnética del campo magnético puede entenderse como debida a un par de polos norte/sur. Los términos de orden superior, como el cuadrupolo, pueden considerarse debidos a 2 o más polos norte/sur ordenados de tal manera que no tienen ninguna contribución de orden inferior. Por ejemplo, la configuración cuadrupolo no tiene momento dipolar neto.
2. δ ³ ( r ) = 0 excepto en r = (0, 0, 0) , por lo que este término se ignora en la expansión multipolar.

Referencias

1. "Relaciones básicas". Geophysics.ou.edu. Archivado desde el original el 9 de julio de 2010. Consultado el 19 de octubre de 2009 .
2. «Campos y fuerzas magnéticas». Archivado desde el original el 20 de febrero de 2012. Consultado el 24 de diciembre de 2009 .
3. "La fuerza producida por un campo magnético". Archivado desde el original el 17 de marzo de 2010. Consultado el 7 de noviembre de 2013 .
4. "Tutorial: Teoría y aplicaciones del tenso de Maxwell" (PDF) . Consultado el 28 de noviembre de 2018 .
5. "Fuerza que actúa sobre las placas de un condensador: recopilación de problemas resueltos". physicstasks.eu . Consultado el 20 de enero de 2020 .
6. Vokoun, David; Beleggia, Marco; Heller, Ludek; Sittner, Petr (2009). "Interacciones magnetostáticas y fuerzas entre imanes permanentes cilíndricos". Revista de magnetismo y materiales magnéticos . 321 (22): 3758–3763. Código Bibliográfico :2009JMMM..321.3758V. doi : 10.1016/j.jmmm.2009.07.030 .
7. Ravaud, R; Lemarquand, G; Babic, S; Lemarquand, V; Akyel, C (2010). "Imanes cilíndricos y bobinas: campos, fuerzas e inductancias". IEEE Transactions on Magnetics . 46 (9): 3585–3590. Bibcode :2010ITM....46.3585R. doi :10.1109/TMAG.2010.2049026. S2CID  25586523.
8. Lehner, Günther (2008). Teoría del campo electromagnético para ingenieros y físicos . p. 309. doi :10.1007/978-3-540-76306-2. ISBN . 978-3-540-76305-5. Número de identificación del sujeto  117970017.
9. Schill, RA (2003). "Relación general para el campo magnético vectorial de un bucle de corriente circular: una mirada más cercana". IEEE Transactions on Magnetics . 39 (2): 961–967. Bibcode :2003ITM....39..961S. doi :10.1109/TMAG.2003.808597.

Véase también

• Motor magnético