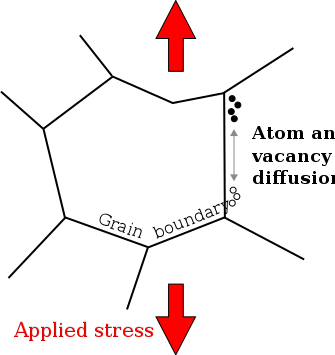
En la ciencia de los materiales , la fluencia de Coble , una forma de fluencia por difusión , es un mecanismo de deformación de sólidos cristalinos . En contraste con otros mecanismos de fluencia por difusión, la fluencia de Coble es similar a la fluencia de Nabarro-Herring en que es dominante a niveles de tensión más bajos y temperaturas más altas que los mecanismos de fluencia que utilizan deslizamiento por dislocación . [1] La fluencia de Coble ocurre a través de la difusión de átomos en un material a lo largo de los límites de grano . Este mecanismo se observa en policristales o a lo largo de la superficie en un monocristal , lo que produce un flujo neto de material y un deslizamiento de los límites de grano.
El científico estadounidense de materiales Robert L. Coble fue el primero en exponer su teoría sobre cómo los materiales se deslizan a través de los límites de grano y a altas temperaturas en alúmina . En este caso, observó un mecanismo de deslizamiento diferente que dependía más del tamaño del grano. [2]
La tasa de deformación en un material que experimenta fluencia de Coble está dada por donde
El deslizamiento de Coble, un mecanismo de difusión, está impulsado por un gradiente de concentración de vacantes (o de masa). El cambio en la concentración de vacantes con respecto a su valor de equilibrio se expresa mediante
Esto se puede ver al observar que y tomando una expansión de alta temperatura, donde el primer término en el lado derecho es la concentración de vacantes debido a la tensión de tracción y el segundo término es la concentración debido a la tensión de compresión. Este cambio en la concentración ocurre perpendicularmente al eje de tensión aplicada, mientras que paralelamente a la tensión no hay cambio en la concentración de vacantes (debido a que la tensión resuelta y el trabajo son cero). [2]
Continuamos asumiendo un grano esférico, para ser consistentes con la derivación para la fluencia de Nabarro-Herring ; sin embargo, absorberemos constantes geométricas en una constante de proporcionalidad . Si consideramos la concentración de vacantes a lo largo del grano bajo una tensión de tracción aplicada, entonces notamos que hay una mayor concentración de vacantes en el ecuador (perpendicular a la tensión aplicada) que en los polos (paralelo a la tensión aplicada). Por lo tanto, existe un flujo de vacantes entre los polos y el ecuador del grano. El flujo de vacantes está dado por la primera ley de Fick en el límite: el coeficiente de difusión por el gradiente de concentración de vacantes. Para el gradiente, tomamos el valor promedio dado por donde hemos dividido la diferencia de concentración total por la longitud de arco entre el ecuador y el polo y luego multiplicamos por el ancho y la longitud del límite .
donde es una constante de proporcionalidad. A partir de aquí, observamos que el cambio de volumen debido a un flujo de vacantes que se difunde desde una fuente de área es el flujo de vacantes multiplicado por el volumen atómico :
donde la segunda igualdad se desprende de la definición de tasa de deformación: . A partir de aquí podemos leer la tasa de deformación:
donde se han absorbido constantes y la difusividad de vacante a través del límite de grano .
La fluencia de Coble y la fluencia de Nabarro-Herring son mecanismos estrechamente relacionados. Ambos son procesos de difusión, impulsados por el mismo gradiente de concentración de vacantes, ocurren en entornos de alta temperatura y baja tensión y sus derivaciones son similares. [1] Para ambos mecanismos, la tasa de deformación es linealmente proporcional a la tensión aplicada y existe una dependencia exponencial de la temperatura. La diferencia es que para la fluencia de Coble, el transporte de masa ocurre a lo largo de los límites de grano, mientras que para Nabarro-Herring la difusión ocurre a través del cristal. Debido a esto, la fluencia de Nabarro-Herring no tiene una dependencia del espesor del límite de grano y tiene una dependencia más débil del tamaño de grano . En la fluencia de Nabarro-Herring, la tasa de deformación es proporcional a en oposición a la dependencia de la fluencia de Coble. Al considerar la tasa de fluencia difusional neta, la suma de ambas tasas de difusión es vital ya que funcionan en procesos paralelos.
La energía de activación para la fluencia de Nabarro-Herring es, en general, diferente a la de la fluencia de Coble. Esto se puede utilizar para identificar qué mecanismo es dominante. Por ejemplo, la energía de activación para la escalada de dislocaciones es la misma que para Nabarro-Herring, por lo que al comparar la dependencia de la temperatura de los regímenes de tensión baja y alta, se puede determinar si la fluencia de Coble o la fluencia de Nabarro-Herring son dominantes. [3]
Los investigadores suelen utilizar estas relaciones para determinar qué mecanismo es dominante en un material; al variar el tamaño del grano y medir cómo se ve afectada la tasa de deformación, pueden determinar el valor de y concluir si el deslizamiento Coble o Nabarro-Herring es dominante. [4]
Bajo estrés moderado a alto, el mecanismo de fluencia dominante ya no es lineal en el estrés aplicado . La fluencia por dislocación, a veces llamada fluencia por ley de potencia (PLC), tiene una dependencia de la ley de potencia en el estrés aplicado que va de 3 a 8. [1] El movimiento de dislocación está relacionado con la estructura atómica y reticular del cristal, por lo que los diferentes materiales responden de manera diferente al estrés, a diferencia de la fluencia de Coble, que siempre es lineal. Esto hace que los dos mecanismos sean fácilmente identificables al encontrar la pendiente de vs .
Tanto el ascenso-deslizamiento por dislocación como el deslizamiento de Coble inducen el deslizamiento de los límites de grano . [1]
Para comprender los regímenes de temperatura y tensión en los que la fluencia de Coble es dominante para un material, es útil observar los mapas de mecanismos de deformación. Estos mapas trazan una tensión normalizada frente a una temperatura normalizada y demarcan dónde los mecanismos de fluencia específicos son dominantes para un material y tamaño de grano determinados (algunos mapas imitan un tercer eje para mostrar el tamaño de grano). Estos mapas solo deben usarse como guía, ya que se basan en ecuaciones heurísticas. [1] Estos mapas son útiles para determinar el mecanismo de fluencia cuando se conocen las tensiones de trabajo y la temperatura para una aplicación con el fin de guiar el diseño del material.
Dado que el deslizamiento de los granos implica el transporte de masa a lo largo de los límites de grano, se formarían grietas o huecos dentro del material sin una acomodación adecuada. El deslizamiento de los límites de grano es el proceso por el cual los granos se mueven para evitar la separación en los límites de grano. [1] Este proceso ocurre típicamente en escalas de tiempo significativamente más rápidas que las de la difusión de masa (un orden de magnitud más rápido). Debido a esto, la velocidad de deslizamiento de los límites de grano es típicamente irrelevante para determinar los procesos del material. Sin embargo, ciertos límites de grano, como los límites coherentes o donde las características estructurales inhiben el movimiento de los límites de grano, pueden ralentizar la velocidad de deslizamiento de los límites de grano hasta el punto en que debe tomarse en consideración. Los procesos subyacentes al deslizamiento de los límites de grano son los mismos que causan el deslizamiento difusional [1]
Este mecanismo fue propuesto originalmente por Ashby y Verrall en 1973 como un deslizamiento por cambio de grano. [5] Esto es competitivo con el deslizamiento de Coble; sin embargo, el cambio de grano dominará en tensiones altas mientras que el deslizamiento de Coble dominará en tensiones bajas.
Este modelo predice una tasa de deformación con la deformación umbral para el cambio de grano . [1]
La relación con el deslizamiento de Coble es clara al observar el primer término, que depende del espesor del límite del grano y del tamaño del grano inverso al cubo .