Afirmando lo consecuente

En lógica proposicional , afirmar el consecuente , a veces llamado error inverso , falacia del inverso o confusión de necesidad y suficiencia , es una falacia formal que consiste en tomar un enunciado condicional verdadero (por ejemplo, "si la lámpara estuviera rota, entonces la habitación estaría oscura") bajo ciertos supuestos (no hay otras luces en la habitación, es de noche y las ventanas están cerradas) e inferir inválidamente su recíproco ("la habitación está oscura, por lo que la lámpara debe estar rota"), aunque ese enunciado pueda no ser verdadero bajo los mismos supuestos. Esto surge cuando el consecuente ("la habitación estaría oscura") tiene otros antecedentes posibles (por ejemplo, "la lámpara está en condiciones de funcionamiento, pero está apagada" o "no hay ninguna lámpara en la habitación"). ^[1]

Los errores inversos son comunes en el pensamiento y la comunicación cotidianos y pueden ser resultado, entre otras causas, de problemas de comunicación, conceptos erróneos sobre la lógica y la falta de consideración de otras causas. ^[2]

La afirmación opuesta, negar el consecuente , se llama modus tollens y es una forma válida de argumento. ^[3]

Descripción formal

Afirmar el consecuente es la acción de tomar una afirmación verdadera y concluir inválidamente su recíproco . El nombre afirmar el consecuente deriva de usar el consecuente, Q , de , para concluir el antecedente P. Esta falacia se puede resumir formalmente como o, alternativamente, . ^[5] La causa fundamental de un error lógico de este tipo es, a veces, no darse cuenta de que, aunque P sea una condición posible para Q , P puede no ser la única condición para Q , es decir, Q puede seguir también de otra condición. ^[6]^[7] $P\to Q$ $Q\a P$ $P\to Q$ $(P\a Q,Q)\a P$ ${\frac {P\to Q,Q}{\por lo tanto P}}$

Afirmar el consecuente también puede resultar de la generalización excesiva de la experiencia de muchas afirmaciones que tienen recíprocos verdaderos. Si P y Q son afirmaciones "equivalentes", es decir , es posible inferir P bajo la condición Q. Por ejemplo, las afirmaciones "Es 13 de agosto, por lo tanto es mi cumpleaños" y "Es mi cumpleaños, por lo tanto es 13 de agosto" son equivalentes y ambas son consecuencias verdaderas de la afirmación "El 13 de agosto es mi cumpleaños" (una forma abreviada de ). 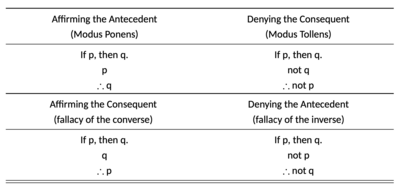$P\leftrightarrow Q$ $P\to Q$ $Q\a P$ $P\leftrightarrow Q$

De las posibles formas de " silogismos hipotéticos mixtos ", dos son válidas y dos no. Afirmar el antecedente ( modus ponens ) y negar el consecuente ( modus tollens ) son válidas. Afirmar el consecuente y negar el antecedente son inválidas. ^[8]

Ejemplos adicionales

Ejemplo 1

Una forma de demostrar la invalidez de esta forma de argumentación es con un contraejemplo con premisas verdaderas pero una conclusión obviamente falsa. Por ejemplo:

Si alguien vive en San Diego , entonces vive en California .

Joe vive en California.

Por lo tanto, Joe vive en San Diego.

Existen muchos lugares para vivir en California además de San Diego. Por otra parte, se puede afirmar con certeza que “si alguien no vive en California” ( no Q ), entonces “esta persona no vive en San Diego” ( no P ). Esta es la contrapositiva de la primera afirmación, y debe ser verdadera si y solo si la afirmación original es verdadera.

Ejemplo 2

Si un animal es un perro, entonces tiene cuatro patas.

Mi gato tiene cuatro patas.

Por lo tanto, mi gato es un perro.

Aquí, resulta inmediatamente intuitivo que cualquier otro número de antecedentes ("Si un animal es un ciervo...", "Si un animal es un elefante...", "Si un animal es un alce...", etc. ) puede dar lugar al consecuente ("entonces tiene cuatro patas"), y que es absurdo suponer que tener cuatro patas debe implicar que el animal es un perro y nada más. Esto es útil como ejemplo didáctico, ya que la mayoría de las personas pueden reconocer inmediatamente que la conclusión a la que se llegó debe ser errónea (intuitivamente, un gato no puede ser un perro) y que, por lo tanto, el método por el que se llegó a ella debe ser falaz.

Ejemplo 3

En Catch-22 , ^[9] el capellán es interrogado por ser supuestamente "Washington Irving"/"Irving Washington", que ha estado bloqueando grandes porciones de cartas enviadas a casa por soldados. El coronel ha encontrado una carta de ese tipo, pero con el nombre del capellán firmado.

—Pero usted sabe leer, ¿no? —insistió el coronel con sarcasmo—. El autor firmó con su nombre.

"Ese es mi nombre allí."

"Entonces lo escribiste. QED "

P en este caso es “El capellán firma con su propio nombre” y Q “El nombre del capellán está escrito”. El nombre del capellán puede estar escrito, pero no necesariamente lo escribió él, como concluye falsamente el coronel. ^[9]

Véase también

Referencias

^ Rosen, Kenneth H. (2019). Matemáticas discretas y sus aplicaciones: Kenneth H. Rosen . McGraw-Hill. ISBN 978-1260091991.
^ Lay, Steven (2014). Introducción al análisis con demostración, quinta edición . Pearson. ISBN 978-0321747471.
^ Hurley, Patrick J. (2012). Una breve introducción a la lógica (11.ª ed.). Boston, Massachusetts: Cengage Learning. pág. 362. ISBN 9781111346232.OCLC 711774631 .
^ Kashef, Arman (2023), En busca de la lógica universal: una breve descripción general de la evolución de la lógica formal, doi :10.13140/RG.2.2.24043.82724/1
^ Hurley, Patrick J. (2010), Una introducción concisa a la lógica (11.ª edición). Wadsworth Cengage Learning, págs. 362–63.
^ "Afirmando lo consecuente". Archivos de falacias . Consultado el 9 de mayo de 2013 .
^ Damer, T. Edward (2001). "Confusión de una condición necesaria con una condición suficiente". Ataque al razonamiento defectuoso (4.ª ed.). Wadsworth. pág. 150. ISBN 0-534-60516-8.
^ Kelley, David (1998), El arte de razonar (3.ª edición). Norton, págs. 290–94.
^ ab Heller, Joseph (1994). Catch-22 . Vintage. págs. 438, 8. ISBN 0-09-947731-9.