La fórmula de Bethe o fórmula de Bethe-Bloch describe la pérdida de energía media por distancia recorrida de partículas cargadas rápidas ( protones , partículas alfa , iones atómicos ) que atraviesan la materia (o alternativamente el poder de frenado del material). [1] Para los electrones, la pérdida de energía es ligeramente diferente debido a su pequeña masa (que requiere correcciones relativistas) y su indistinguibilidad , y dado que sufren pérdidas mucho mayores por Bremsstrahlung , se deben agregar términos para tener esto en cuenta. Las partículas cargadas rápidas que se mueven a través de la materia interactúan con los electrones de los átomos en el material. La interacción excita o ioniza los átomos, lo que lleva a una pérdida de energía de la partícula que viaja.
La versión no relativista fue encontrada por Hans Bethe en 1930; la versión relativista (que se muestra a continuación) fue encontrada por él en 1932. [2] La pérdida de energía más probable difiere de la pérdida de energía media y se describe mediante la distribución de Landau-Vavilov. [3]
Para una partícula con velocidad v , carga z (en múltiplos de la carga del electrón) y energía E , que viaja una distancia x hacia un objetivo con densidad de número de electrones n y energía de excitación media I (ver más abajo), la versión relativista de la fórmula se lee, en unidades del SI: [2]
donde c es la velocidad de la luz y ε 0 la permitividad del vacío , , e y m e la carga del electrón y la masa en reposo respectivamente.
Aquí, la densidad electrónica del material se puede calcular mediante
donde ρ es la densidad del material, Z su número atómico , A su masa atómica relativa , N A el número de Avogadro y M u la constante de masa molar .
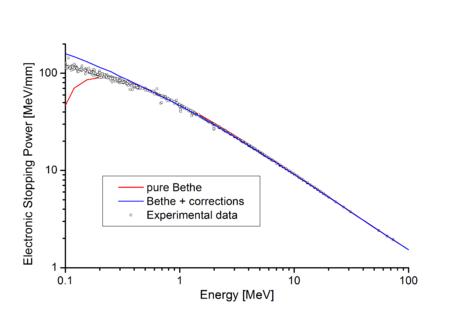
En la figura de la derecha, los círculos pequeños son resultados experimentales obtenidos a partir de mediciones de varios autores, mientras que la curva roja es la fórmula de Bethe. [4] Evidentemente, la teoría de Bethe concuerda muy bien con los experimentos a alta energía. La concordancia es aún mejor cuando se aplican correcciones (ver más abajo).
Para energías bajas, es decir, para pequeñas velocidades de la partícula β << 1, la fórmula de Bethe se reduce a
Esto se puede ver reemplazando primero βc por v en la ecuación (1) y luego descuidando β 2 debido a su pequeño tamaño.
Por lo tanto, a baja energía, la pérdida de energía según la fórmula de Bethe disminuye aproximadamente como v −2 con el aumento de la energía. Alcanza un mínimo para aproximadamente E = 3 Mc 2 , donde M es la masa de la partícula (para los protones, esto sería alrededor de 3000 MeV). Para casos altamente relativistas β ≈ 1, la pérdida de energía aumenta nuevamente, logarítmicamente debido al componente transversal del campo eléctrico.

En la teoría de Bethe, el material se describe completamente mediante un único número, la energía de excitación media I . En 1933, Felix Bloch demostró que la energía de excitación media de los átomos está dada aproximadamente por
donde Z es el número atómico de los átomos del material. Si se introduce esta aproximación en la fórmula ( 1 ) anterior, se obtiene una expresión que a menudo se denomina fórmula de Bethe-Bloch . Pero como ahora tenemos tablas precisas de I en función de Z (ver más abajo), el uso de dicha tabla arrojará mejores resultados que el uso de la fórmula ( 3 ).
La figura muestra valores normalizados de I , tomados de una tabla. [5] Los picos y valles en esta figura conducen a valles y picos correspondientes en el poder de frenado. Estos se denominan " Z 2 -oscilaciones" o " Z 2 -estructura" (donde Z 2 = Z significa el número atómico del objetivo).
La fórmula de Bethe sólo es válida para energías lo suficientemente altas como para que la partícula atómica cargada (el ion ) no lleve consigo ningún electrón atómico. A energías más bajas, cuando el ion lleva electrones, esto reduce efectivamente su carga y, por lo tanto, se reduce el poder de frenado. Pero incluso si el átomo está completamente ionizado, son necesarias correcciones.
Bethe encontró su fórmula usando la teoría de perturbaciones de la mecánica cuántica . Por lo tanto, su resultado es proporcional al cuadrado de la carga z de la partícula. La descripción se puede mejorar considerando correcciones que corresponden a potencias mayores de z . Estas son: el efecto Barkas-Andersen (proporcional a z 3 , según Walter H. Barkas y Hans Henrik Andersen ), y la corrección de Felix Bloch (proporcional a z 4 ). Además, hay que tener en cuenta que los electrones atómicos del material atravesado no son estacionarios (" corrección de capas ").
Las correcciones mencionadas se han incorporado a los programas PSTAR y ASTAR, por ejemplo, con los que se puede calcular el poder de frenado de los protones y las partículas alfa. [6] Las correcciones son grandes a baja energía y se vuelven cada vez más pequeñas a medida que aumenta la energía.
A energías muy altas, hay que añadir la corrección de densidad de Fermi [5] .