Supervisión débil

Un paradigma en el aprendizaje automático

La supervisión débil es un paradigma en el aprendizaje automático , cuya relevancia y notoriedad aumentaron con la llegada de grandes modelos de lenguaje debido a la gran cantidad de datos necesarios para entrenarlos. Se caracteriza por utilizar una combinación de una pequeña cantidad de datos etiquetados por humanos (utilizados exclusivamente en el paradigma de aprendizaje supervisado más costoso y que requiere más tiempo ), seguido de una gran cantidad de datos no etiquetados (utilizados exclusivamente en el paradigma de aprendizaje no supervisado ). En otras palabras, los valores de salida deseados se proporcionan solo para un subconjunto de los datos de entrenamiento. Los datos restantes no están etiquetados o están etiquetados de manera imprecisa. Intuitivamente, se puede ver como un examen y los datos etiquetados como problemas de muestra que el profesor resuelve para la clase como ayuda para resolver otro conjunto de problemas. En el entorno transductivo , estos problemas sin resolver actúan como preguntas de examen. En el entorno inductivo , se convierten en problemas de práctica del tipo que conformarán el examen. Técnicamente, podría verse como realizar una agrupación y luego etiquetar los grupos con los datos etiquetados, alejando el límite de decisión de las regiones de alta densidad o aprendiendo una variedad unidimensional subyacente donde residen los datos.

Problema

Tendencia de una tarea a emplear métodos supervisados ​​y no supervisados. Los nombres de las tareas que se encuentran entre los límites del círculo son intencionales. Esto demuestra que la división clásica de las tareas imaginativas (izquierda) que emplean métodos no supervisados ​​está desdibujada en los esquemas de aprendizaje actuales.

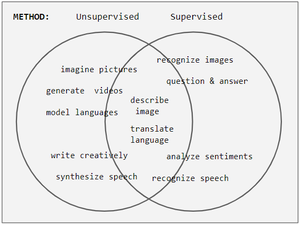
La adquisición de datos etiquetados para un problema de aprendizaje a menudo requiere un agente humano capacitado (por ejemplo, para transcribir un segmento de audio) o un experimento físico (por ejemplo, determinar la estructura 3D de una proteína o determinar si hay petróleo en una ubicación particular). El costo asociado con el proceso de etiquetado puede hacer que los conjuntos de entrenamiento grandes y completamente etiquetados sean inviables, mientras que la adquisición de datos no etiquetados es relativamente económica. En tales situaciones, el aprendizaje semisupervisado puede ser de gran valor práctico. El aprendizaje semisupervisado también es de interés teórico en el aprendizaje automático y como modelo para el aprendizaje humano.

Técnica

Un ejemplo de la influencia de los datos no etiquetados en el aprendizaje semisupervisado. El panel superior muestra un límite de decisión que podríamos adoptar después de ver solo un ejemplo positivo (círculo blanco) y uno negativo (círculo negro). El panel inferior muestra un límite de decisión que podríamos adoptar si, además de los dos ejemplos etiquetados, se nos diera una colección de datos no etiquetados (círculos grises).

De manera más formal, el aprendizaje semisupervisado supone que se procesa un conjunto de ejemplos distribuidos de forma idéntica e independiente con las etiquetas correspondientes y ejemplos no etiquetados . El aprendizaje semisupervisado combina esta información para superar el rendimiento de clasificación que se puede obtener descartando los datos no etiquetados y realizando un aprendizaje supervisado o descartando las etiquetas y realizando un aprendizaje no supervisado. ${\displaystyle l}$ ${\displaystyle x_{1},\dots ,x_{l}\in X}$ ${\displaystyle y_{1},\dots ,y_{l}\in Y}$ ${\displaystyle u}$ ${\displaystyle x_{l+1},\dots ,x_{l+u}\in X}$

El aprendizaje semisupervisado puede referirse tanto al aprendizaje transductivo como al aprendizaje inductivo . ^[1] El objetivo del aprendizaje transductivo es inferir las etiquetas correctas solo para los datos no etiquetados dados. El objetivo del aprendizaje inductivo es inferir la asignación correcta de a . ${\displaystyle x_{l+1},\dots ,x_{l+u}}$ ${\displaystyle X}$ ${\displaystyle Y}$

No es necesario (y, según el principio de Vapnik , imprudente) realizar aprendizaje transductivo infiriendo una regla de clasificación sobre todo el espacio de entrada; sin embargo, en la práctica, los algoritmos diseñados formalmente para la transducción o la inducción a menudo se usan indistintamente.

Supuestos

Para poder utilizar datos no etiquetados, debe existir alguna relación con la distribución subyacente de los datos. Los algoritmos de aprendizaje semisupervisado utilizan al menos uno de los siguientes supuestos: ^[2]

Supuesto de continuidad/suavidad

Los puntos que están cerca entre sí tienen más probabilidades de compartir una etiqueta. Esto también se supone generalmente en el aprendizaje supervisado y produce una preferencia por límites de decisión geométricamente simples . En el caso del aprendizaje semisupervisado, el supuesto de suavidad produce además una preferencia por límites de decisión en regiones de baja densidad, por lo que pocos puntos están cerca entre sí pero en diferentes clases. ^[3]

Supuesto de agrupamiento

Los datos tienden a formar grupos discretos y es más probable que los puntos de un mismo grupo compartan una etiqueta (aunque los datos que comparten una etiqueta pueden estar distribuidos en varios grupos). Este es un caso especial del supuesto de uniformidad y da lugar al aprendizaje de características con algoritmos de agrupamiento.

Supuesto múltiple

Los datos se encuentran aproximadamente en una variedad de dimensión mucho menor que el espacio de entrada. En este caso, el aprendizaje de la variedad utilizando tanto los datos etiquetados como los no etiquetados puede evitar la maldición de la dimensionalidad . Luego, el aprendizaje puede continuar utilizando distancias y densidades definidas en la variedad.

El supuesto de variedad es práctico cuando los datos de alta dimensión se generan mediante algún proceso que puede ser difícil de modelar directamente, pero que tiene solo unos pocos grados de libertad. Por ejemplo, la voz humana está controlada por unas pocas cuerdas vocales ^[4] y las imágenes de varias expresiones faciales están controladas por unos pocos músculos. En estos casos, es mejor considerar las distancias y la suavidad en el espacio natural del problema generador, en lugar de en el espacio de todas las ondas acústicas o imágenes posibles, respectivamente.

Historia

El enfoque heurístico de autoentrenamiento (también conocido como autoaprendizaje o autoetiquetado ) es históricamente el enfoque más antiguo para el aprendizaje semisupervisado, ^[2] con ejemplos de aplicaciones que comienzan en la década de 1960. ^[5]

El marco de aprendizaje transductivo fue introducido formalmente por Vladimir Vapnik en la década de 1970. ^[6] El interés en el aprendizaje inductivo utilizando modelos generativos también comenzó en la década de 1970. Ratsaby y Venkatesh demostraron en 1995 un límite de aprendizaje probablemente aproximadamente correcto para el aprendizaje semisupervisado de una mezcla gaussiana. [ ^7]

Métodos

Modelos generativos

Los enfoques generativos del aprendizaje estadístico primero buscan estimar [ ^{disputado – discutir ] la} distribución de los puntos de datos que pertenecen a cada clase. La probabilidad de que un punto dado tenga una etiqueta es entonces proporcional a por la regla de Bayes . El aprendizaje semisupervisado con modelos generativos puede verse como una extensión del aprendizaje supervisado (clasificación más información sobre ) o como una extensión del aprendizaje no supervisado (agrupamiento más algunas etiquetas). ${\displaystyle p(x|y)}$ ${\displaystyle p(y|x)}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle p(x|y)p(y)}$ ${\displaystyle p(x)}$

Los modelos generativos suponen que las distribuciones adoptan una forma particular parametrizada por el vector . Si estas suposiciones son incorrectas, los datos no etiquetados pueden, en realidad, reducir la precisión de la solución en relación con lo que se habría obtenido con datos etiquetados únicamente. ^[8] Sin embargo, si las suposiciones son correctas, entonces los datos no etiquetados necesariamente mejoran el rendimiento. ^[7] ${\displaystyle p(x|y,\theta )}$ ${\displaystyle \theta }$

Los datos no etiquetados se distribuyen de acuerdo con una mezcla de distribuciones de clases individuales. Para conocer la distribución de mezcla a partir de los datos no etiquetados, esta debe ser identificable, es decir, los diferentes parámetros deben producir diferentes distribuciones sumadas. Las distribuciones de mezcla gaussianas son identificables y se utilizan comúnmente para los modelos generativos.

La distribución conjunta parametrizada se puede escribir como mediante la regla de la cadena . Cada vector de parámetros se asocia con una función de decisión . Luego, el parámetro se elige en función del ajuste a los datos etiquetados y no etiquetados, ponderado por : ${\displaystyle p(x,y|\theta )=p(y|\theta )p(x|y,\theta )}$ ${\displaystyle \theta }$ ${\displaystyle f_{\theta }(x)={\underset {y}{\operatorname {argmax} }}\ p(y|x,\theta )}$ ${\displaystyle \lambda }$

${\displaystyle {\underset {\Theta }{\operatorname {argmax} }}\left(\log p(\{x_{i},y_{i}\}_{i=1}^{l}|\theta )+\lambda \log p(\{x_{i}\}_{i=l+1}^{l+u}|\theta )\right)}$^[9]

Separación de baja densidad

Otra clase importante de métodos intenta colocar límites en regiones con pocos puntos de datos (etiquetados o no etiquetados). Uno de los algoritmos más utilizados es la máquina de vectores de soporte transductiva o TSVM (que, a pesar de su nombre, también se puede utilizar para el aprendizaje inductivo). Mientras que las máquinas de vectores de soporte para el aprendizaje supervisado buscan un límite de decisión con un margen máximo sobre los datos etiquetados, el objetivo de TSVM es un etiquetado de los datos no etiquetados de modo que el límite de decisión tenga un margen máximo sobre todos los datos. Además de la pérdida de bisagra estándar para los datos etiquetados, se introduce una función de pérdida sobre los datos no etiquetados al dejar . Luego, TSVM selecciona de un espacio de Hilbert de kernel de reproducción minimizando el riesgo empírico regularizado : ${\displaystyle (1-yf(x))_{+}}$ ${\displaystyle (1-|f(x)|)_{+}}$ ${\displaystyle y=\operatorname {sign} {f(x)}}$ ${\displaystyle f^{*}(x)=h^{*}(x)+b}$ ${\displaystyle {\mathcal {H}}}$

${\displaystyle f^{*}={\underset {f}{\operatorname {argmin} }}\left(\displaystyle \sum _{i=1}^{l}(1-y_{i}f(x_{i}))_{+}+\lambda _{1}\|h\|_{\mathcal {H}}^{2}+\lambda _{2}\sum _{i=l+1}^{l+u}(1-|f(x_{i})|)_{+}\right)}$

Una solución exacta es intratable debido al término no convexo , por lo que la investigación se centra en aproximaciones útiles. ^[9] ${\displaystyle (1-|f(x)|)_{+}}$

Otros enfoques que implementan la separación de baja densidad incluyen modelos de procesos gaussianos, regularización de información y minimización de entropía (de los cuales TSVM es un caso especial).

Regularización laplaciana

La regularización laplaciana se ha abordado históricamente a través del método laplaciano de grafos. Los métodos basados ​​en grafos para el aprendizaje semisupervisado utilizan una representación gráfica de los datos, con un nodo para cada ejemplo etiquetado y no etiquetado. El grafo se puede construir utilizando el conocimiento del dominio o la similitud de ejemplos; dos métodos comunes son conectar cada punto de datos con sus vecinos más cercanos o con ejemplos dentro de cierta distancia . El peso de un borde entre y se establece entonces en . ${\displaystyle k}$ ${\displaystyle \epsilon }$ ${\displaystyle W_{ij}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$ ${\displaystyle e^{-\|x_{i}-x_{j}\|^{2}/\epsilon ^{2}}}$

En el marco de la regularización de variedades , ^{[10] [11]} el grafo sirve como proxy de la variedad. Se añade un término al problema de regularización de Tikhonov estándar para reforzar la suavidad de la solución en relación con la variedad (en el espacio intrínseco del problema) así como en relación con el espacio de entrada ambiental. El problema de minimización se convierte en

${\displaystyle {\underset {f\in {\mathcal {H}}}{\operatorname {argmin} }}\left({\frac {1}{l}}\displaystyle \sum _{i=1}^{l}V(f(x_{i}),y_{i})+\lambda _{A}\|f\|_{\mathcal {H}}^{2}+\lambda _{I}\int _{\mathcal {M}}\|\nabla _{\mathcal {M}}f(x)\|^{2}dp(x)\right)}$^[9]

donde es un espacio de Hilbert de núcleo reproductor y es la variedad en la que se encuentran los datos. Los parámetros de regularización y controlan la suavidad en los espacios ambiente e intrínseco respectivamente. El gráfico se utiliza para aproximar el término de regularización intrínseca. Definiendo el gráfico laplaciano donde y es el vector , tenemos ${\displaystyle {\mathcal {H}}}$ ${\displaystyle {\mathcal {M}}}$ ${\displaystyle \lambda _{A}}$ ${\displaystyle \lambda _{I}}$ ${\displaystyle L=D-W}$ ${\displaystyle D_{ii}=\sum _{j=1}^{l+u}W_{ij}}$ ${\displaystyle \mathbf {f} }$ ${\displaystyle [f(x_{1})\dots f(x_{l+u})]}$

${\displaystyle \mathbf {f} ^{T}L\mathbf {f} =\displaystyle \sum _{i,j=1}^{l+u}W_{ij}(f_{i}-f_{j})^{2}\approx \int _{\mathcal {M}}\|\nabla _{\mathcal {M}}f(x)\|^{2}dp(x)}$.

El enfoque basado en gráficos para la regularización laplaciana es ponerlo en relación con el método de diferencias finitas . ^{[ aclaración necesaria ] [ cita necesaria ]}

El laplaciano también se puede utilizar para extender los algoritmos de aprendizaje supervisado: mínimos cuadrados regularizados y máquinas de vectores de soporte (SVM) a versiones semisupervisadas de mínimos cuadrados regularizados laplacianos y SVM laplacianos.

Enfoques heurísticos

Algunos métodos de aprendizaje semisupervisado no están intrínsecamente orientados al aprendizaje tanto de datos etiquetados como no etiquetados, sino que hacen uso de datos no etiquetados dentro de un marco de aprendizaje supervisado. Por ejemplo, los ejemplos etiquetados y no etiquetados pueden informar una elección de representación, métrica de distancia o kernel para los datos en un primer paso no supervisado. Luego, el aprendizaje supervisado procede solo de los ejemplos etiquetados. En esta línea, algunos métodos aprenden una representación de baja dimensión utilizando los datos supervisados ​​y luego aplican métodos de separación de baja densidad o basados ​​en gráficos a la representación aprendida. ^{[12] [13]} Refinar iterativamente la representación y luego realizar un aprendizaje semisupervisado en dicha representación puede mejorar aún más el rendimiento. ${\displaystyle x_{1},\dots ,x_{l+u}}$

El autoentrenamiento es un método de envoltorio para el aprendizaje semisupervisado. ^[14] Primero, se entrena un algoritmo de aprendizaje supervisado basándose únicamente en los datos etiquetados. Luego, este clasificador se aplica a los datos no etiquetados para generar más ejemplos etiquetados como entrada para el algoritmo de aprendizaje supervisado. Generalmente, en cada paso solo se agregan las etiquetas en las que el clasificador tiene más confianza. ^[15] En el procesamiento del lenguaje natural, un algoritmo de autoentrenamiento común es el algoritmo de Yarowsky para problemas como la desambiguación del sentido de las palabras, la restauración del acento y la corrección ortográfica. ^[16]

El co-entrenamiento es una extensión del auto-entrenamiento en el cual múltiples clasificadores se entrenan en diferentes conjuntos (idealmente disjuntos) de características y generan ejemplos etiquetados para cada uno. ^[17]

En la cognición humana

Las respuestas humanas a los problemas formales de aprendizaje semisupervisado han dado lugar a conclusiones diversas sobre el grado de influencia de los datos no etiquetados. ^[18] Los problemas de aprendizaje más naturales también pueden considerarse ejemplos de aprendizaje semisupervisado. Gran parte del aprendizaje de conceptos humanos implica una pequeña cantidad de instrucción directa (por ejemplo, el etiquetado de objetos por parte de los padres durante la infancia) combinada con grandes cantidades de experiencia no etiquetada (por ejemplo, la observación de objetos sin nombrarlos ni contarlos, o al menos sin retroalimentación).

Los bebés humanos son sensibles a la estructura de categorías naturales no etiquetadas, como imágenes de perros y gatos o rostros masculinos y femeninos. ^[19] Los bebés y los niños tienen en cuenta no sólo los ejemplos no etiquetados, sino también el proceso de muestreo del que surgen los ejemplos etiquetados. ^{[20] [21]}

Véase también

• Aprendizaje de PU

Referencias

1. Encuesta de literatura sobre aprendizaje semisupervisado, página 5 , 2007, CiteSeerX  10.1.1.99.9681
2. Chapelle, Schölkopf y Zien 2006.
3. Chawla, N., Bowyer, K., Hall, LO y Kegelmeyer, WP (2002). SMOTE: Técnica sintética de sobremuestreo de minorías. ArXiv, abs/1106.1813.
4. Stevens, Kenneth N. (1998). Fonética acústica . Cambridge, Mass.: MIT Press. ISBN 0-585-08720-2.OCLC 42856189  .
5. Scudder, H. (julio de 1965). "Probabilidad de error de algunas máquinas de reconocimiento de patrones adaptativo". IEEE Transactions on Information Theory . 11 (3): 363–371. doi :10.1109/TIT.1965.1053799. ISSN  1557-9654.
6. Vapnik, V.; Chervonenkis, A. (1974). Teoría del reconocimiento de patrones (en ruso). Moscú: Nauka.citado en Chapelle, Schölkopf & Zien 2006, p. 3
7. Ratsaby, J.; Venkatesh, S. "Aprendizaje de una mezcla de ejemplos etiquetados y no etiquetados con información lateral paramétrica" ​​(PDF) .en Actas de la octava conferencia anual sobre teoría del aprendizaje computacional - COLT '95 . Nueva York, Nueva York, EE. UU.: ACM Press. 1995. págs. 412–417. doi :10.1145/225298.225348. ISBN 0-89791-723-5. Número de identificación del sujeto  17561403.. Citado en Chapelle, Schölkopf & Zien 2006, p. 4
8. Fabio, Cozman; Ira, Cohen (22 de septiembre de 2006), "Riesgos del aprendizaje semisupervisado: cómo los datos no etiquetados pueden degradar el rendimiento de los clasificadores generativos", Semi-Supervised Learning , The MIT Press, págs. 56-72, doi :10.7551/mitpress/9780262033589.003.0004, ISBN 978-0-262-03358-9En: Chapelle, Schölkopf y Zien 2006
9. Zhu, Xiaojin. Aprendizaje semisupervisado Universidad de Wisconsin-Madison.
10. M. Belkin; P. Niyogi (2004). "Aprendizaje semisupervisado en variedades de Riemann". Machine Learning . 56 (Número especial sobre agrupamiento): 209–239. doi : 10.1023/b:mach.0000033120.25363.1e .
11. M. Belkin, P. Niyogi, V. Sindhwani. Sobre la regularización de variedades. AISTATS 2005.
12. Iscen, Ahmet; Tolias, Giorgos; Avrithis, Yannis; Chum, Ondrej (2019). "Propagación de etiquetas para aprendizaje semisupervisado profundo". Conferencia IEEE/CVF de 2019 sobre visión artificial y reconocimiento de patrones (CVPR) . págs. 5065–5074. arXiv : 1904.04717 . doi :10.1109/CVPR.2019.00521. ISBN . 978-1-7281-3293-8. S2CID  104291869 . Consultado el 26 de marzo de 2021 .
13. Burkhart, Michael C.; Shan, Kyle (2020). "Separación profunda de baja densidad para clasificación semisupervisada". International Conference on Computational Science (ICCS) . Apuntes de clase en informática. Vol. 12139. págs. 297–311. arXiv : 2205.11995 . doi : 10.1007/978-3-030-50420-5_22 . ISBN . 978-3-030-50419-9.
14. Triguero, Isaac; García, Salvador; Herrera, Francisco (2013-11-26). "Técnicas autoetiquetadas para aprendizaje semisupervisado: taxonomía, software y estudio empírico". Conocimiento y Sistemas de Información . 42 (2): 245–284. doi :10.1007/s10115-013-0706-y. ISSN  0219-1377. S2CID  1955810.
15. Fazakis, Nikos; Karlos, Stamatis; Kotsiantis, Sotiris; Sgarbas, Kyriakos (29 de diciembre de 2015). "LMT autodidacta para aprendizaje semisupervisado". Inteligencia Computacional y Neurociencia . 2016 : 3057481. doi : 10.1155/2016/3057481 . PMC 4709606 . PMID  26839531. 
16. Yarowsky, David (1995). "Unsupervised Word Sense Disambiguation Rivaling Supervised Methods". Actas de la 33.ª Reunión Anual de la Asociación de Lingüística Computacional . Cambridge, MA: Asociación de Lingüística Computacional: 189–196. doi : 10.3115/981658.981684 . Consultado el 1 de noviembre de 2022 .
17. Didaci, Luca; Fumera, Giorgio; Roli, Fabio (7 de noviembre de 2012). Gimel'farb, Georgy; Hancock, Edwin; Imiya, Atsushi; Kuijper, Arjan; Kudo, Mineichi; Omachi, Shinichiro; Windeatt, Terry; Yamada, Keiji (eds.). Análisis de algoritmos de coentrenamiento con conjuntos de entrenamiento muy pequeños . Notas de clase en informática. Springer Berlin Heidelberg. págs. 719–726. doi :10.1007/978-3-642-34166-3_79. ISBN . 9783642341656.S2CID 46063225  .
18. Zhu, Xiaojin (2009). Introducción al aprendizaje semisupervisado . Goldberg, AB (Andrew B.). [San Rafael, California]: Morgan & Claypool Publishers. ISBN 978-1-59829-548-1.OCLC 428541480  .
19. Younger BA; Fearing DD (1999). "Análisis de elementos en categorías separadas: cambio de desarrollo en la categorización infantil". Desarrollo infantil . 70 (2): 291–303. doi :10.1111/1467-8624.00022.
20. Xu, F. y Tenenbaum, JB (2007). "Sensibilidad al muestreo en el aprendizaje de palabras bayesiano". Developmental Science . 10 (3): 288–297. CiteSeerX 10.1.1.141.7505 . doi :10.1111/j.1467-7687.2007.00590.x. PMID  17444970. 
21. Gweon, H., Tenenbaum JB y Schulz LE (2010). "Los bebés consideran tanto la muestra como el proceso de muestreo en la generalización inductiva". Proc Natl Acad Sci USA . 107 (20): 9066–71. Bibcode :2010PNAS..107.9066G. doi : 10.1073/pnas.1003095107 . PMC 2889113 . PMID  20435914. {{cite journal}}: CS1 maint: multiple names: authors list (link)

Fuentes

• Chapelle, Olivier; Schölkopf, Bernhard; Zien, Alejandro (2006). Aprendizaje semisupervisado . Cambridge, Massachusetts: MIT Press. ISBN 978-0-262-03358-9.

Enlaces externos

• Regularización de variedades Una implementación MATLAB disponible gratuitamente de los algoritmos semisupervisados ​​basados ​​en gráficos, máquinas de vectores de soporte laplacianas y mínimos cuadrados regularizados laplacianos.
• KEEL: Herramienta de software para evaluar algoritmos evolutivos para problemas de Minería de Datos (regresión, clasificación, clustering, minería de patrones, etc.) Módulo KEEL para aprendizaje semi-supervisado.
• Software de aprendizaje semisupervisado
• Aprendizaje semisupervisado: documentación de scikit-learn Aprendizaje semisupervisado en scikit-learn .