¿Se puede diseccionar cada simplex en un número limitado de ortoesquemas?
En geometría, es una conjetura no resuelta de Hugo Hadwiger que cada simplex puede ser disecado en ortoesquemas , utilizando un número de ortosquemas limitados por una función de la dimensión del simplex. [1] Si es cierto, entonces, de manera más general, cada politopo convexo podría diseccionarse en ortosquemas.
En este contexto, un espacio euclidiano simplex en dimensiones es el casco convexo de puntos que no todos se encuentran en un hiperplano común . Por ejemplo, un simplex bidimensional es simplemente un triángulo (el casco convexo de tres puntos en el plano) y un simplex tridimensional es un tetraedro (el convexo de cuatro puntos en el espacio tridimensional). Los puntos que forman el simplex de esta forma se llaman sus vértices .
Un ortoesquema, también llamado camino simplex, es un tipo especial de simplex. En él, los vértices se pueden conectar mediante un camino , de modo que cada dos bordes del camino formen ángulos rectos entre sí. Un ortosquema bidimensional es un triángulo rectángulo . Se puede construir un ortoesquema tridimensional a partir de un cubo encontrando un camino de tres aristas del cubo que no se encuentran todos en la misma cara cuadrada y formando el casco convexo de los cuatro vértices en este camino.

Una disección de una forma (que puede ser cualquier conjunto cerrado en el espacio euclidiano) es una representación de una unión de otras formas cuyos interiores están separados entre sí . Es decir, intuitivamente, las formas de la unión no se superponen, aunque pueden compartir puntos en sus límites. Por ejemplo, un cubo se puede diseccionar en seis ortoesquemas tridimensionales. Un resultado similar se aplica de manera más general: cada hipercubo o hiperrectángulo en dimensiones se puede diseccionar en ortoesquemas.
La conjetura de Hadwiger es que existe una función tal que cada simplex -dimensional puede diseccionarse en la mayoría de los ortoesquemas. Hadwiger planteó este problema en 1956; [2] sigue sin resolverse en general, aunque se conocen casos especiales para valores pequeños de. [1]
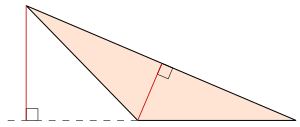
En dos dimensiones, cada triángulo se puede dividir en como máximo dos triángulos rectángulos, reduciendo una altitud desde su ángulo más amplio hasta su borde más largo. [2]
En tres dimensiones, algunos tetraedros se pueden diseccionar de manera similar, reduciendo una altitud perpendicularmente desde un vértice a un punto en una cara opuesta, conectando perpendicularmente a los lados de la cara y usando los caminos perpendiculares de tres bordes a través y hacia un lado y luego a un vértice de la cara. [2] Sin embargo, esto no siempre funciona. En particular, existen tetraedros para los cuales ninguno de los vértices tiene altitudes con un pie dentro de la cara opuesta. Utilizando una construcción más complicada, Lenhard (1960) demostró que cada tetraedro puede diseccionarse en como máximo 12 ortoesquemas. [3] Böhm (1980) demostró que esto es óptimo: existen tetraedros que no pueden diseccionarse en menos de 12 ortoesquemas. [4] En el mismo artículo, Böhm también generalizó el resultado de Lenhard a geometría esférica tridimensional y geometría hiperbólica tridimensional .
En cuatro dimensiones se necesitan como máximo 500 ortoesquemas. [5] En cinco dimensiones, nuevamente se necesita un número finito de ortoesquemas, aproximadamente limitado a 12,5 millones como máximo. Nuevamente, esto se aplica a la geometría esférica y a la geometría hiperbólica, así como a la geometría euclidiana. [6]
La conjetura de Hadwiger sigue sin demostrarse para todas las dimensiones mayores que cinco. [1]
Cada politopo convexo puede diseccionarse en símplex. Por tanto, si la conjetura de Hadwiger es cierta, todo politopo convexo también tendría una disección en ortosquemas. [6]
Un resultado relacionado es que cada ortoesquema puede diseccionarse en ortoesquemas más pequeños. [7] [8] Por lo tanto, para los simples que pueden dividirse en ortosquemas, sus disecciones pueden tener un número arbitrariamente grande de ortosquemas.