
La línea de fonón cero y la banda lateral de fonón constituyen conjuntamente la forma de línea de moléculas individuales que absorben y emiten luz ( cromóforos ) incrustadas en una matriz sólida transparente. Cuando la matriz anfitriona contiene muchos cromóforos, cada uno contribuirá con una línea de fonón cero y una banda lateral de fonón a los espectros de absorción y emisión . Se dice que los espectros que se originan a partir de una colección de cromóforos idénticos en una matriz están ensanchados de manera no homogénea porque cada cromóforo está rodeado por un entorno de matriz algo diferente que modifica la energía requerida para una transición electrónica. En una distribución no homogénea de cromóforos, las posiciones individuales de la línea de fonón cero y la banda lateral de fonón están, por lo tanto, desplazadas y superpuestas.
La figura 1 muestra la forma típica de la línea para las transiciones electrónicas de cromóforos individuales en una matriz sólida. La línea de fonón cero se encuentra en una frecuencia ω' determinada por la diferencia intrínseca en los niveles de energía entre el estado fundamental y el estado excitado, así como por el entorno local. La banda lateral del fonón se desplaza a una frecuencia más alta en la absorción y a una frecuencia más baja en la fluorescencia. La brecha de frecuencia Δ entre la línea de fonón cero y el pico de la banda lateral del fonón está determinada por los principios de Franck-Condon .
La distribución de intensidad entre la línea de fonón cero y la banda lateral de fonón depende en gran medida de la temperatura. A temperatura ambiente hay suficiente energía térmica para excitar muchos fonones y la probabilidad de transición de fonón cero es cercana a cero. Para cromóforos orgánicos en matrices orgánicas, la probabilidad de una transición electrónica de fonón cero solo se vuelve probable por debajo de aproximadamente 40 kelvin , pero también depende de la fuerza del acoplamiento entre el cromóforo y la red anfitriona.

La transición entre el estado fundamental y el excitado se basa en el principio de Franck-Condon , que establece que la transición electrónica es muy rápida en comparación con el movimiento en la red. Las transiciones de energía pueden simbolizarse entonces mediante flechas verticales entre el estado fundamental y el excitado, es decir, no hay movimiento a lo largo de las coordenadas configuracionales durante la transición. La figura 2 es un diagrama de energía para interpretar la absorción y emisión con y sin fonones en términos de la coordenada configuracional . Las transiciones de energía se originan en el nivel de energía de fonón más bajo de los estados electrónicos. Como se representa en la figura, la mayor superposición de funciones de onda (y, por lo tanto, la mayor probabilidad de transición) ocurre cuando la energía del fotón es igual a la diferencia de energía entre los dos estados electrónicos ( ) más tres cuantos de energía vibracional del modo reticular ( ). Esta transición de tres fonones se refleja en la emisión cuando el estado excitado decae rápidamente a su nivel de vibración reticular de punto cero por medio de un proceso sin radiación, y desde allí al estado fundamental a través de la emisión de fotones. La transición de fonón cero se describe como si tuviera una superposición de función de onda menor y, por lo tanto, una probabilidad de transición menor.
Además de la hipótesis de Franck-Condon, se suelen suponer otras tres aproximaciones que están implícitas en las figuras. La primera es que cada modo vibracional de la red está bien descrito por un oscilador armónico cuántico . Esta aproximación está implícita en la forma parabólica de los pozos de potencial de la Figura 2 y en el espaciamiento de energía igual entre los niveles de energía de los fonones. La segunda aproximación es que solo se excita la vibración de red más baja (punto cero). Esto se denomina aproximación de baja temperatura y significa que las transiciones electrónicas no se originan en ninguno de los niveles de fonones superiores. La tercera aproximación es que la interacción entre el cromóforo y la red es la misma tanto en el estado fundamental como en el excitado. Específicamente, el potencial del oscilador armónico es igual en ambos estados. Esta aproximación, llamada acoplamiento lineal, está representada en la Figura 2 por dos potenciales parabólicos de forma igual y por niveles de energía de fonones igualmente espaciados tanto en el estado fundamental como en el excitado.
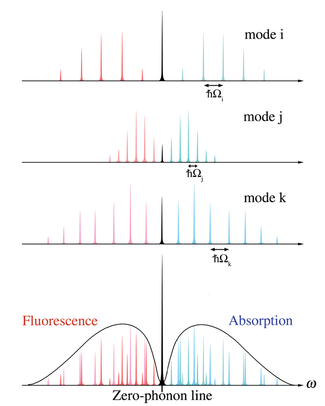
La fuerza de la transición de fonón cero surge de la superposición de todos los modos de red. Cada modo de red tiene una frecuencia vibratoria característica que conduce a una diferencia de energía entre fonones . Cuando se suman las probabilidades de transición para todos los modos, las transiciones de fonón cero siempre se suman en el origen electrónico ( ), mientras que las transiciones con fonones contribuyen en una distribución de energías. La Figura 3 ilustra la superposición de probabilidades de transición de varios modos de red. Las contribuciones de transición de fonón de todos los modos de red constituyen la banda lateral de fonón.
La separación de frecuencia entre los máximos de las bandas laterales de fonones de absorción y fluorescencia es la contribución del fonón al desplazamiento de Stokes .
La forma de la línea de fonón cero es lorentziana con un ancho determinado por el tiempo de vida del estado excitado T 10 de acuerdo con el principio de incertidumbre de Heisenberg . Sin la influencia de la red, el ancho de línea natural (ancho completo a la mitad del máximo) del cromóforo es γ 0 = 1/ T 10 . La red reduce el tiempo de vida del estado excitado al introducir mecanismos de desintegración sin radiación. En el cero absoluto , el tiempo de vida del estado excitado influenciado por la red es T 1 . Por encima del cero absoluto, los movimientos térmicos introducirán perturbaciones aleatorias en el entorno local de los cromóforos. Estas perturbaciones desplazan la energía de la transición electrónica, introduciendo un ensanchamiento del ancho de línea dependiente de la temperatura. El ancho medido de la línea de fonón cero de un solo cromóforo, el ancho de línea homogéneo, es entonces γ h ( T ) ≥ 1/ T 1 .
La forma de la línea de la banda lateral del fonón es la de una distribución de Poisson , ya que expresa un número discreto de eventos, transiciones electrónicas con fonones, durante un período de tiempo. A temperaturas más altas, o cuando el cromóforo interactúa fuertemente con la matriz, la probabilidad de multifonón es alta y la banda lateral del fonón se aproxima a una distribución gaussiana .
La distribución de intensidad entre la línea del fonón cero y la banda lateral del fonón se caracteriza por el factor de Debye-Waller α.
La línea de fonón cero es una analogía óptica de las líneas de Mössbauer , que se originan en la emisión o absorción sin retroceso de rayos gamma de los núcleos de átomos unidos en una matriz sólida. En el caso de la línea óptica de fonón cero, la posición del cromóforo es el parámetro físico que puede ser perturbado, mientras que en la transición gamma, los momentos de los átomos pueden cambiar. Más técnicamente, la clave de la analogía es la simetría entre la posición y el momento en el hamiltoniano del oscilador armónico cuántico . Tanto la posición como el momento contribuyen de la misma manera (cuadráticamente) a la energía total.